图神经网络解偏微分方程系列(一)
作者:互联网
图神经网络解偏微分方程系列(一)
1. 标题和概述
Learning continuous-time PDEs from sparse(稀疏) data with graph neural networks
使用图神经网络从稀疏数据中学习连续时间偏微分方程
这篇文章是使用图神经网络从稀疏数据中学习连续时间偏微分方程,发表在ICLR,ICLR是深度学习的顶级会议。
文章提出的模型主要创新点是允许任意空间和时间离散化,也就是说在求解偏微分划分网格时,网格可以是不均匀的,由于所求解的控制方程是未知的,在表示控制方程时,作者使用了消息传递的图神经网络进行参数化。与之前的基于机器学习的PDE方法(数据驱动)比较:PINN虽然求得的方程的解,在时间上是连续的,但是它求的方程是已知的,并且在空间邻域和边界条件都不是自由的。PDE-Net虽然需要学习的方程是未知的,但是求得的解不是连续时间的,在空间邻域和边界条件都不是自由的。这篇文章提出的方法能同时保证通过数据学习未知的偏微分方程,解在时间上是连续的,并且空间邻域和边界条件都是自由的。
文章所用的模型是基于直线法,把偏微分方程化成常微分方程组,常微分方程组右边的项用消息传递的图神经网络来表示,在构造图结构时,进行了Delaunay三角剖分,Delaunay三角剖分具有空圆特性和使每个三角形最小角度最大化。
2. 文章链接
Learning continuous-time PDEs from sparse data with graph neural networks
3. 作者
Valerii Iakovlev, Markus Heinonen & Harri Lahdesmaki
4. 出版杂志及日期
Published as a conference paper at ICLR 2021
5. 摘要
许多动力系统的行为遵循复杂的,但仍然未知的偏微分方程。虽然已经提出了几种机器学习方法来直接从数据中学习偏微分方程,但以前的方法仅限于离散时间近似,或者使观测到达规则网格的有限假设。我们提出了一种广义连续时间微分动力学模型,该模型的控制方程是通过消息传递的图神经网络参数化的。该模型允许任意的空间和时间离散化,消除了对观测点位置和观测间隔的限制。模型采用连续时间伴随方法(continuous-time adjoint method)进行训练,实现了高效的神经PDE推理。我们展示了该模型处理非结构化网格、任意时间步长和噪声观测的能力。我们将我们的方法与一些知名物理系统的现有方法进行了比较,这些物理系统包括一阶和高阶偏微分方程,具有最先进的预测性能。
6. 总结
我们提出了一个动力系统的连续时间模型,其行为受偏微分方程控制。该模型能准确地恢复系统的动态,即使观测点稀疏且记录的时间间隔不规律。与离散时间模型的比较揭示了连续时间模型对于观测之间时间间隔较大的数据集的优势,这在实际应用中是典型的,因为在实际应用中,测量可能是乏味的或昂贵的,或两者兼有。用直线法(method of lines)离散坐标域提供了一个通用的建模框架,在该框架中,可以使用任意的替代函数来逼近 。该模型的连续时间特性使得从欧拉方法(Euler method)到高度精确的自适应方法(adaptive methods)的各种时间积分器(time integrators)得以使用。这允许根据数据的结构优化代理函数(surrogate function)和时间集成方案(time integration scheme)的选择。
。该模型的连续时间特性使得从欧拉方法(Euler method)到高度精确的自适应方法(adaptive methods)的各种时间积分器(time integrators)得以使用。这允许根据数据的结构优化代理函数(surrogate function)和时间集成方案(time integration scheme)的选择。
7. 贡献
在本文中,我们从稀疏数据出发提出了学习一个自由形式、连续时间、先验完全未知的PDE模型F,稀疏数据被测量使用图神经网络在坐标邻域 的任意时间点和位置上。我们的贡献是:
的任意时间点和位置上。我们的贡献是:
- 我们引进了PDE驱动系统(PDE-driven systems)的连续时间表示和学习
- 我们提出了使用带消息传递神经网络(message passing neural networks)的直线方法(method of lines)来有效的表示域结构(domain structure)的图
- 我们在具有不规则数据的真实PDE系统上取得了最先进的学习性能,并且我们的模型对数据稀疏性具有高度的鲁棒性
可以在这个github储存库中找到用于复制实验的脚本和数据。
8. 实验
我们评估我们的模型在学习已知物理系统动力学方面的表现。我们比较了最先进的可竞争的方法,并开始进行消融研究(ablation studies)以衡量我们模型的性能如何依赖于测量网格大小、观测间隔、不规则采样、数据量和噪声量。
8.1 对流扩散消融研究(convection-diffusion ablation studies)
对流扩散方程是一个偏微分方程,可以用来模拟与物理系统中粒子、能量和其他物理量的传递有关的各种物理现象。这种转移是由对流和扩散两个过程引起的。对流-扩散方程的定义为
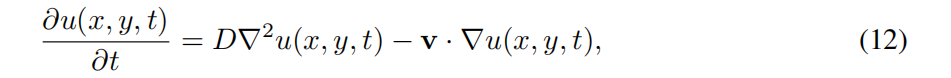
其中 是一些兴趣量的集中(the concentration of some quantity of interest),利用观测状态
是一些兴趣量的集中(the concentration of some quantity of interest),利用观测状态 和估计状态
和估计状态 之间的相对误差来评估模型的预测质量:
之间的相对误差来评估模型的预测质量:

在接下来的所有实验中,除非另有说明,训练数据包含时间间隔[0,0.2]秒的24个模拟,测试数据包含时间间隔[0,0.6]秒的50个模拟。从高保真仿真中随机下采样数据,因此所有的训练和测试仿真都有不同节点位置,而节点数量保持不变。图14显示了来自训练和测试集的示例,
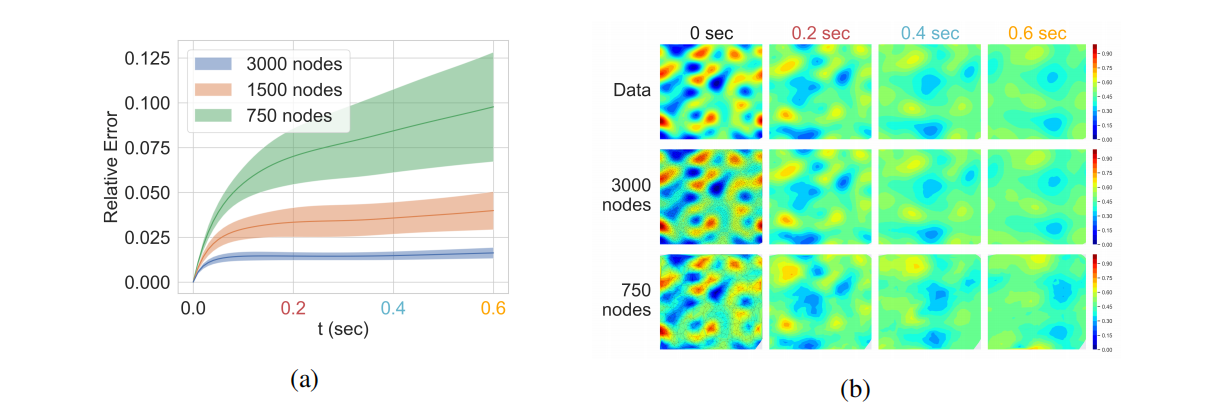
不同网格大小。 这个实验测试了我们的模型从观测点不同密度的数据学习能力。时间步长被设置为0.02秒,导致每个模型有11个训练时间点。观测点 的数目(和GNN中的节点)被设置为3000,1500,750。结果网格显示在图2b的第一列中。图2显示了相关的测试误差和模型的预测。
的数目(和GNN中的节点)被设置为3000,1500,750。结果网格显示在图2b的第一列中。图2显示了相关的测试误差和模型的预测。
模型的性能随着网格中节点数目减少而降低。尽管如此,即使使用最小的网格,模型也能够学习到一个合理准确的系统动力学近似,并在训练时间间隔之外进行推广。
不同的测试时间间隔。 如下面的实验所示,具有常数时间步长的模型对观测间隔的长度是敏感的。当时间步长较小时,该模型表现出良好的性能,但是当时间步长增大时,该模型无法推广。这个实验显示了我们的模型在观测时间间隔相对较长的情况下从数据中学习的能力。
我们使用11、4和2个均匀的时间点进行训练。节点的设置为3000。图3显示了相对测试误差和模型的预测。该模型能恢复系统的连续时间动力学,即使在每个仿真中用四个时间点训练。增加观察频率并不会显著提高性能。图中显示了一个带有四个时间点的训练模型示意。
不规则的时间步长。 用于训练的观察结果可能不是用固定的时间步长记录的。这可能会给基于这种假设构建的模型带来麻烦。这个实验测试了我们模型在随机时间点学习被观测到数据的能力。
模型在两个时间网格上训练。第一个网格具有恒定的时间步长0.02秒。第二个网格与第一个网格相同,但每个时间点都受到噪声的干扰 。这给出了一个不规则时间步长设置0.01秒。节点数目设置为3000。相对测设误差如图4所示,在这两种情况下,模型实现了相似的性能。这证明了我们模型的连续时间特性,因为训练和预测不像大多数其他方法那样局限于均匀间隔的时间网格。没有一个以前的方法学习自由形式(即参数化神经网络)的PDE可以使用随时间不规则采样的数据进行训练。
。这给出了一个不规则时间步长设置0.01秒。节点数目设置为3000。相对测设误差如图4所示,在这两种情况下,模型实现了相似的性能。这证明了我们模型的连续时间特性,因为训练和预测不像大多数其他方法那样局限于均匀间隔的时间网格。没有一个以前的方法学习自由形式(即参数化神经网络)的PDE可以使用随时间不规则采样的数据进行训练。

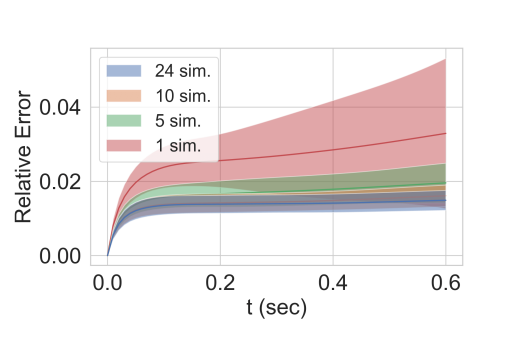
不同的数据量。 在本实验中,对模型进行了1,5,10,24次模拟训练。测试数据包含50个模拟。节点数目设置为3000。相对测试误差如图5所示。模型的性能随着训练数据量的增加而提高。值得注意的是,尽管使用了更多的数据,相对误差并不收敛到零。
不同数量的附加噪声。 我们应用附加噪声 训练数据,其中
训练数据,其中 设置为0.02和0.04,而观测状态的最大量值为1。时间步长设置为0.01秒。节点数设置为3000。噪声只添加到训练数据中。相关测设误差如图6所示。模型的性能随着
设置为0.02和0.04,而观测状态的最大量值为1。时间步长设置为0.01秒。节点数设置为3000。噪声只添加到训练数据中。相关测设误差如图6所示。模型的性能随着 的增大而降低,但
的增大而降低,但 时模型仍保持较高的性能。
时模型仍保持较高的性能。

8.2 基准方法比较(Banchmark method conparison)
将本文提出的方法与文献中提出的两个模型进行比较:PDE-Net (Long et al., 2017)和DPGN(Seo & LIu, 2019a)。PDE-Net是基于卷积神经网络,采用类似欧拉方法的不变时间步长方案(constant time-stepping scheme)。DPGN是基于图神经网络,实现了时间步长作为潜在空间的进化图(an evolution map in the latent space)。
我们使用(long et al., 2017)等人提供的PDE-Net实现,除此之外,我们传递滤波值(filter value)通过一个MLP(多层感知机),MLP被组成由2个隐藏层,每层60个神经元,非线性激活函数为tanh,这有助于提高模型的稳定性和性能。我们使用无矩约束(without moment constraints) 和
和 的滤波器,最大偏微分方程的阶数分别为4和2。
的滤波器,最大偏微分方程的阶数分别为4和2。 的数量设置为训练数据中的时间步长。我们对DPGN的实现遵循从(Seo & Liu, 2019)其潜扩散系数(latent diffusivity)
的数量设置为训练数据中的时间步长。我们对DPGN的实现遵循从(Seo & Liu, 2019)其潜扩散系数(latent diffusivity) 。所有模型的参数数接近20K。
。所有模型的参数数接近20K。
训练数据包含24个模拟在时间间隔[0,0.2]秒,遵循的时间步长如下:0.01,0.02和0.04。测试数据包含50个在时间间隔[0,0.6]秒上的模拟,遵循的时间步长相同。由于PDE-Net不能应用于任意的空间网格,数据生成在 的规则网格上。每个时间步数分别训练不同的模型。模型的性能是用相对测试误差随时间平均的平均值来评估的。
的规则网格上。每个时间步数分别训练不同的模型。模型的性能是用相对测试误差随时间平均的平均值来评估的。

模型的平均相对测试误差如图7所示。由图可知离散时间模型的性能对时间步长具有很强的依赖性,而连续时间模型的性能能保持在同一水平。在最小的时间步长下,PDE-Net  滤波器的性能优于其他模型,这是因为PDE-Net能够访问更大的节点领域,使得模型能够做出更准确的预测。然而,较大的滤波器尺寸不能提高稳定性。
滤波器的性能优于其他模型,这是因为PDE-Net能够访问更大的节点领域,使得模型能够做出更准确的预测。然而,较大的滤波器尺寸不能提高稳定性。
我们注意到一些离散时间模型,例如,DPGN,可以修改为将时间步长作为其输入。与这种类型的模型进行比较是多余的,因为图7已经演示了这种模型的最佳情况下的性能(当使用恒定时间步长进行训练和测试时)。
相对位置信息的重要性。我们在不同节点数量的网格上使用或不使用相对节点位置(relative node position)作为边缘特征编码(encoded as the edge features)的MPNN来测试模型。节点数量越少,相邻节点之间的距离变化(distance variability)越高(图12),这应该会增加模型精度对相对空间信息的依赖。通过从模型中删除空间信息,我们恢复了GNODE。模型在热量和对流扩散方程上进行了测试。实验的完整描述在附录D中,结果如图8所示。

令人惊讶的是,GNODE在纯扩散热方程上显示了良好的结果。尽管如此,GNODE显著的性能明显不同于我们的模型,包括空间信息。而且,当节点数量从100%减少到50%时,性能差异几乎翻倍。


当将GNODE应用于对流扩散方程时,无论节点数量如何,GNODE都无法学习动力学。这可以用对流项的存在来解释,对流项将场向特定方向输送,因此,位置信息对于准确预测场的变化尤为重要。
8.3 其他动力系统(other dynamical systems)
该模型在另外两个动力系统上进行了测试,以评估其处理更广泛问题的能力。为此,我们选择了热方程(heat equation)和Burgers' 方程。热方程是最简单的偏微分方程之一,而由于非线性对流项的存在,Burgers方法比对流扩散方程更为复杂。随着问题难度的增加,我们可以在保持模型参数数量不变的情况下,跟踪从简单到复杂的动态过程中模型性能的变化。
热方程。 热方程描述了扩散系统的行为。方程定义为 ,其中u为温度场。图9显示了一个随机测试情况的相对误差和模型预测。热方程比对流扩散方程描述的动力学更简单,这使得模型可以获得略小的测试误差。
,其中u为温度场。图9显示了一个随机测试情况的相对误差和模型预测。热方程比对流扩散方程描述的动力学更简单,这使得模型可以获得略小的测试误差。
Burgers' 方程。 Burgers方程是由两个耦合的非线性方程组(coupled nonlinear PDEs)组成的方程组。它描述了具有非线性传播效应(nonlinear propagation effects)的耗散系统(dissipative systems)的行为。方程定义为 ,其中
,其中 是速度向量场。为了可视化误差和测量的目的,速度向量场被转换为由每个节点的的速度大小定义的标量场。图10显示了一个随机测试例子的相对误差和模型预测。
是速度向量场。为了可视化误差和测量的目的,速度向量场被转换为由每个节点的的速度大小定义的标量场。图10显示了一个随机测试例子的相对误差和模型预测。
Burgers' 方程 描述的动力学比前两种情况更复杂,反映在较高的相对测试误差。真实状态和预测状态的视觉对比表明,该模型能够在逼近未知动态时达到足够的精度。
9 方法
在本节中,我们考虑从观测中学习未知函数 的问题,从系统状态
的问题,从系统状态 的观测
的观测 在
在 个任意空间位置
个任意空间位置 ,
, 个时间点
个时间点 。我们引入有效的图卷积神经网络替代在连续时间从稀疏数据学习偏微分方程。注意,当我们考虑任意采样的空间位置和时间点时,我们不考虑部分观测向量
。我们引入有效的图卷积神经网络替代在连续时间从稀疏数据学习偏微分方程。注意,当我们考虑任意采样的空间位置和时间点时,我们不考虑部分观测向量 的情况,即在某个位置的数据在某个时间点丢失。然而,在计算损失时,部分观测向量可以通过掩盖观测缺失的节点来计算。假设函数
的情况,即在某个位置的数据在某个时间点丢失。然而,在计算损失时,部分观测向量可以通过掩盖观测缺失的节点来计算。假设函数 不依赖于空间坐标的全局值(global values of the spatial coordinates),即假设系统不包含位置相关的场(position-dependent fields)。
不依赖于空间坐标的全局值(global values of the spatial coordinates),即假设系统不包含位置相关的场(position-dependent fields)。

我们采用直线法(method of lines, MOL) (Schiesser, 2012)对式1进行数值计算。MOL包括在 中选择
中选择 个节点,并在这些节点上离散
个节点,并在这些节点上离散 的空间导数。我们将节点放置到观测位置
的空间导数。我们将节点放置到观测位置 。离散化导致
。离散化导致 被
被 近似,并产生下列常微分方程组(ODE),其解渐近地近似于方程1的解
近似,并产生下列常微分方程组(ODE),其解渐近地近似于方程1的解
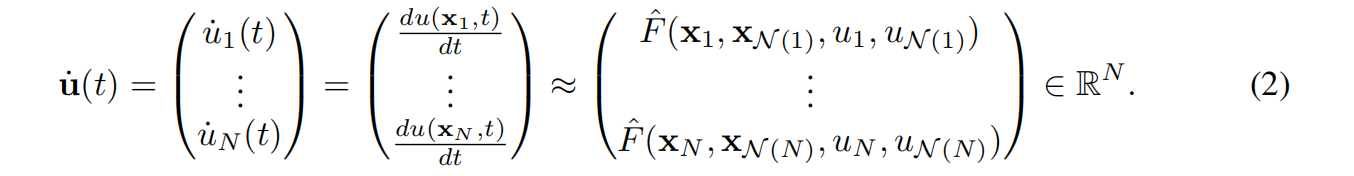
由于离散化的 从从真实的PDE函数
从从真实的PDE函数 继承了它的未知性质,我们用一个可学习的神经网络替代函数来近似
继承了它的未知性质,我们用一个可学习的神经网络替代函数来近似 。
。
系统在 处的状态被定义为
处的状态被定义为 ,而
,而 是一组除了
是一组除了 的相邻节点的指标,这些指标要求
的相邻节点的指标,这些指标要求 在
在 处求值,
处求值, 和
和 是节点
是节点 的位置和状态。由此可见,
的位置和状态。由此可见, 的时间倒数
的时间倒数 不仅于节点的位置和状态有关,而且还与相邻节点的位置和状态有关,从而形成一个局部耦合的ODE系统
不仅于节点的位置和状态有关,而且还与相邻节点的位置和状态有关,从而形成一个局部耦合的ODE系统
系统中的每个ODE都遵循一个固定位置 的解。已经提出了许多ODE求解器(如Euler和Runge-Kutta求解器)来求解整个系统
的解。已经提出了许多ODE求解器(如Euler和Runge-Kutta求解器)来求解整个系统

其中 是一个积累的中间时间变量。在时间尺度上线性地向前求解方程3关于节点数
是一个积累的中间时间变量。在时间尺度上线性地向前求解方程3关于节点数 和评估时间点的数量
和评估时间点的数量 ,而饱和输入空间(saturating the input sapce)
,而饱和输入空间(saturating the input sapce)  需要大量节点。在实际应用中,偏微分方程通常应用于二维和三维空间系统中,这种方法是有效的。
需要大量节点。在实际应用中,偏微分方程通常应用于二维和三维空间系统中,这种方法是有效的。
9.1 位置不变的图神经网络微分
在引入方程2之后,我们从学习 过渡到学习
过渡到学习 。
。 在节点
在节点 处的值必须仅依赖于节点
处的值必须仅依赖于节点 和
和 。此外,
。此外, 的参数数量和它们的顺序是事先不知道的,对于每个节点可能是不同的。这意味着我们的模型
的参数数量和它们的顺序是事先不知道的,对于每个节点可能是不同的。这意味着我们的模型 必须能够处理任意数量的参数,并且必须对它们的顺序不变。图神经网络(GNNs)(Wu et al., 2020)满足这些要求。在一个更受限的设置中,邻居的数量和它们的顺序是已知的(例如,如果网格是均匀的),其他类型的模型,例如多层感知机和卷积神经网络也可以使用。
必须能够处理任意数量的参数,并且必须对它们的顺序不变。图神经网络(GNNs)(Wu et al., 2020)满足这些要求。在一个更受限的设置中,邻居的数量和它们的顺序是已知的(例如,如果网格是均匀的),其他类型的模型,例如多层感知机和卷积神经网络也可以使用。
我们考虑一种图神经网络称为消息传递神经网络(message passing neural networks, MPNNs) (Gilmer et al., 2017),将 表示为
表示为

其中
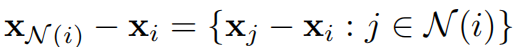
 表示MPNN的参数。
表示MPNN的参数。
该公式假设 中没有位置相关的量,但基于该公式的模型对
中没有位置相关的量,但基于该公式的模型对 的平移和旋转不变,这使得对具有不同节点位置的系统的推广是可行的,并通过记忆特定位置的动力学(memorizing position-specific dynamic)防止过拟合。
的平移和旋转不变,这使得对具有不同节点位置的系统的推广是可行的,并通过记忆特定位置的动力学(memorizing position-specific dynamic)防止过拟合。
由于其灵活性和计算效率,我们使用了一种基于空间的GNN。主要基于可替代谱的GNNs(alternative-spectral-based GNN)——在节点数量上具有相对较差的伸缩性,并且需要学习全局或依赖于领域的滤波器,由于需要对拉普拉斯矩阵进行特征值分解。
9.2 消息传递神经网络
设图 包含节点
包含节点 ,由测量位置定义,无向边
,由测量位置定义,无向边 ,并且假设每个节点和边缘分别与一个节点特征
,并且假设每个节点和边缘分别与一个节点特征 和一个边缘特征
和一个边缘特征 相关联。我们使用节点邻域
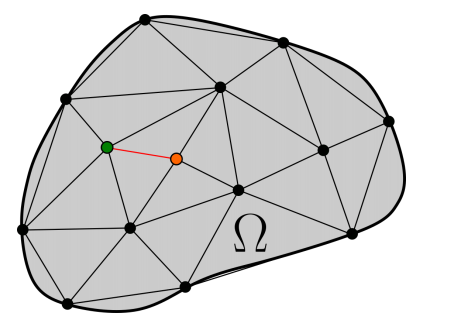
相关联。我们使用节点邻域 来定义边。通过对测量位置进行Delaunay三角剖分,选择每个节点的邻居。两个节点被认为是邻居,如果它们至少在一个三角形的同一条边上(图1)。Delaunay三角剖分具有使每个三角形的最小角度最大化在三角剖分中和包含每个节点的最近邻等有用特征,有助于获得
来定义边。通过对测量位置进行Delaunay三角剖分,选择每个节点的邻居。两个节点被认为是邻居,如果它们至少在一个三角形的同一条边上(图1)。Delaunay三角剖分具有使每个三角形的最小角度最大化在三角剖分中和包含每个节点的最近邻等有用特征,有助于获得 的良好离散性。
的良好离散性。
在消息传递图神经网络中,我们传播 个图层的潜在状态(latent state),其中每一层
个图层的潜在状态(latent state),其中每一层 首先由每个节点
首先由每个节点 的聚合消息
的聚合消息 组成,然后更新相应的节点状态
组成,然后更新相应的节点状态

其中 表示置换不变的聚合函数(如sum,mean,max),
表示置换不变的聚合函数(如sum,mean,max), ,
, 是由神经网络参数化的可微函数。在任何时间
是由神经网络参数化的可微函数。在任何时间 ,我们初始化潜在状态
,我们初始化潜在状态 和节点特征到当前系统的状态
和节点特征到当前系统的状态 。我们定义边缘特征
。我们定义边缘特征 为位置差异。最后,我们使用MPNN图层(graph layer of the MPNN)的最后一个节点状态来评估PDE替代函数(PDE surrogate)。
为位置差异。最后,我们使用MPNN图层(graph layer of the MPNN)的最后一个节点状态来评估PDE替代函数(PDE surrogate)。

用于求解方程3的估计状态
9.3 学习连续时间MPNN替代的伴随方法(adjoint method)
 的参数由
的参数由 定义,
定义, 是函数
是函数 ,
, 的参数联合(the union of parameters),
的参数联合(the union of parameters), 在MPNN中。我们通过最小化观测状态
在MPNN中。我们通过最小化观测状态 和估计状态
和估计状态 间的均方误差来拟合
间的均方误差来拟合
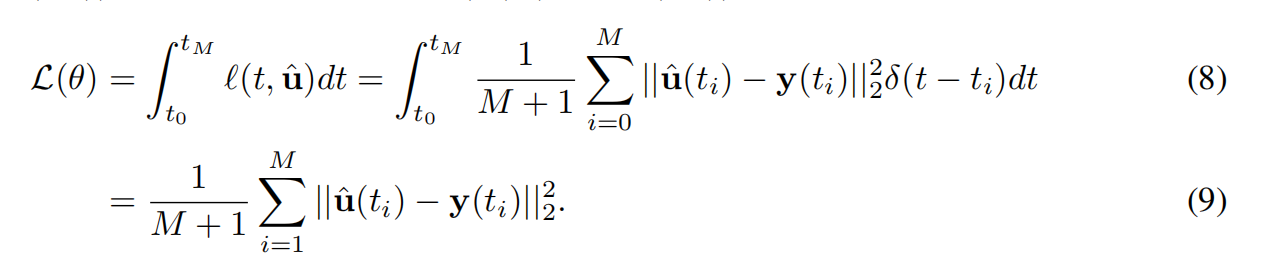
虽然离散时间神经PDE模型仅在测量时间点评估系统状态,但对于估计状态的更精确的连续时间解通常需要更多的系统状态评估。如果使用自适应求解器(adaptive solver)来获得估计的状态,求解器执行的时间步长数量可能显著大于 。通过反向传播来评估
。通过反向传播来评估 的梯度所需内存数量与求解器时间步长数量成线性比例。由于大量内存需求,这通常使得反向传播不可行。我们使用另一种方法,它允许计算内存开销的梯度,这与求解器的时间步长无关。(Chen et al. (2018))提出了这种方法称为神经ODEs(neural ODEs),基于(Pontryagin, 2018)的伴随方法(the adjoint method)。伴随方法由一个单层前馈ODE通道3直到最后时间
的梯度所需内存数量与求解器时间步长数量成线性比例。由于大量内存需求,这通常使得反向传播不可行。我们使用另一种方法,它允许计算内存开销的梯度,这与求解器的时间步长无关。(Chen et al. (2018))提出了这种方法称为神经ODEs(neural ODEs),基于(Pontryagin, 2018)的伴随方法(the adjoint method)。伴随方法由一个单层前馈ODE通道3直到最后时间 在最后状态
在最后状态 ,随后反向传播ODE计算梯度。反向传播是通过先解伴随方程来完成的。
,随后反向传播ODE计算梯度。反向传播是通过先解伴随方程来完成的。

对伴随变量 从
从 到
到 ,其中
,其中 ,然后计算
,然后计算

来得到最终的梯度。

10 介绍(Introduction)
我们考虑状态 随时间
随时间 而演化,空间位置
而演化,空间位置 的有界邻域
的有界邻域 的连续动力系统。我们假定系统由一个未知的偏微分方程(PDE)控制
的连续动力系统。我们假定系统由一个未知的偏微分方程(PDE)控制

系统的时间演化 依赖于当前的状态
依赖于当前的状态 和它的空间一阶和高阶偏导数关于坐标
和它的空间一阶和高阶偏导数关于坐标 。这种PDE模型是自然科学的基石,广泛适用于传播系统的建模,如声波行为、流体动力学、散热、天气模式、疾病进展或细胞动力学(Courant & Hilbert, 2008)。我们的目标是从数据中学习微分
。这种PDE模型是自然科学的基石,广泛适用于传播系统的建模,如声波行为、流体动力学、散热、天气模式、疾病进展或细胞动力学(Courant & Hilbert, 2008)。我们的目标是从数据中学习微分 。
。
对于特定的系统(Cajori, 1928)手工推导机械的偏微分方程已有很长的历史,如Navier-Stokes流体动力或Schrodinger的量子方程,并在时间上逼近它们的解(Ames, 2014)。这些努力由数据驱动的方法加以补充,以推断已知方程中的任何未知或潜在系数(Isakov, 2006; Berg & Nystrom, 2017; Santo et al., 2019),或部分已知的方程(Freund et al., 2019; Seo & Liu, 2019b; Seo et al., 2020)。一系列方法研究了已知偏微分方程的解加速神经替代(neural proxies) (Lagaris et al., 1998; Raissi et al., 2017; Weinan & Yu, 2018;Sirignano & Spiliopoulos, 2018)或不确定性量化(uncertainty quantification) (Khoo et al., 2017)。
相关的工作。 最近(Long et al. (2017))的开创新工作提出了一种完全非机械化方法PDE-Net,其中控制方程 是从系统快照中学习的,作为一个卷积神经网络(CNN)在输入域离散成一个时空网格(spatio-temporal)。进一步的工作扩展了残差CNNs(Ruthotto & Haber, 2019][]),符号回归神经网络(Long et al., 2019),高阶自回归网络(high-order autoregressive network) (Geneva & Zabaras, 2020),前馈网络(Xu et al., 2019)。这些模型基本上局限于离散输入域的采样效率低的网格,同时它们也不支持随时间的持续演化,使得它们无法处理在现实应用中经常遇到的时间或空间上稀疏不均匀的观测。
是从系统快照中学习的,作为一个卷积神经网络(CNN)在输入域离散成一个时空网格(spatio-temporal)。进一步的工作扩展了残差CNNs(Ruthotto & Haber, 2019][]),符号回归神经网络(Long et al., 2019),高阶自回归网络(high-order autoregressive network) (Geneva & Zabaras, 2020),前馈网络(Xu et al., 2019)。这些模型基本上局限于离散输入域的采样效率低的网格,同时它们也不支持随时间的持续演化,使得它们无法处理在现实应用中经常遇到的时间或空间上稀疏不均匀的观测。
模型如(Battaglia et al., 2016; Chang et al., 2016; Sanchez-Gonzalez et al., 2018)对象的状态演化为其相邻对象函数的交互网络有关(the interaction networks where object's state evolves as a function of its neighboring objects),形成动态关系图而不是网格。与密集的PDE解域(the dense solution fields of PDEs)不同,这些模型在少量移动和交互对象之间应用消息传递,这与严格意义上的微分函数PDE不同。
(Poli et all. (2019))提出了图神经常微分方程(graph neural ordinary differential equations, GNODE)作为在图上建模连续时间型号的框架。该框架应用于学习偏微分方程的主要局限性是缺乏关于物理节点位置的空间信息以及缺乏这种类型模型适合的动机。我们的工作可以看作是通过经典的偏微分方程求解技术将基于图的连续时间模型与数据驱动的空间偏微分方程联系起来。
11 方法梳理
考虑一个动力系统其状态 ,其中
,其中 ,
, ,
,
数据:
- 时间点

- 观测点

- 观测状态
 ,其中
,其中
假设系统是由方程
所掌控。

模型是基于直线法:
例子,考虑PDE: |
|---|
 |
 |

一般地,考虑PDE: |
|---|
 |
 |

把 表示为
表示为

即
References:
V. Iakovlev, M. Heinonen, and H. Lähdesmäki, “Learning continuous-time PDEs from sparse data with graph neural networks,” arXiv:2006.08956 [cs, stat], Jan. 2021, Accessed: Oct. 11, 2021. [Online]. Available: http://arxiv.org/abs/2006.08956
标签:解偏,步长,模型,网格,神经网络,时间,微分方程,PDE,节点 来源: https://www.cnblogs.com/guodongsanjianke/p/15413949.html

