因果推断-解决推荐系统公平性的新思路

论文引入

近年来推荐系统公平性成为新的热点，在所有解决公平性问题的方法中，因果推断显得格外靓眼。我们以论文《Recommendations as treatments: Debiasing learning and evaluation》^[1]做为引入，来看看因果推断是怎么应用在推荐系统公平性研究中的。
改论文的思想如下：从因果推断的角度看待推荐问题，我们可以认为在推荐系统中给用户曝光某个商品类似于在医学中给病人施加某种治 疗方式。这两个任务的共同点是，只知道少数病人(用户)对少数治疗方式(物品) 的反应，而大多数的病人-治疗(用户-物品)对的结果是观察不到的。下图是电影爱好者的评分情况。

第一行依次为：真实的评分矩阵\(Y\)、倾向矩阵\(P\)、观察示性矩阵\(O\)；第二行依次为：两个评分预测矩阵\(Y_1\)和\(Y_2\)，介入示性矩阵\(Y_3\)。
可以看到，我们只能统计到少数用户给商品的评分。对于没有被曝光的商品，我们将无法获得其评分数据。
接下来我们定量地分析。用户-物品可以全部观测时的方法如下式所示，即理想状况下的评测标准指标。\(\delta_{u,i}(Y, \hat{Y})\)可以取平方误差、0-1误差等。

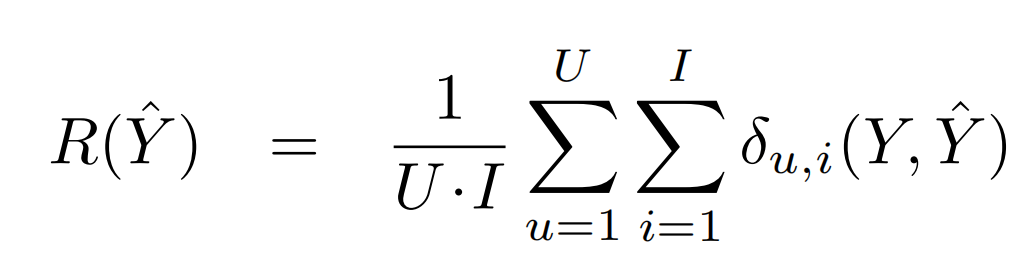
用户-物品对可以部分观测时评测的方法如下式所示。

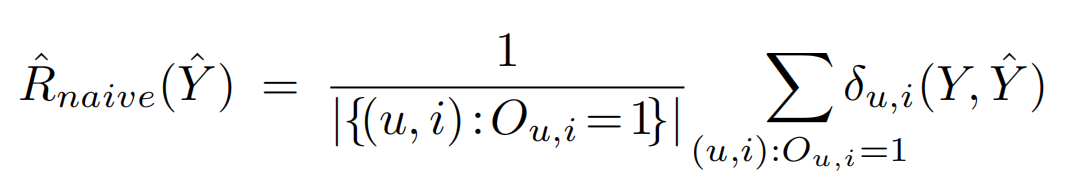
我们设\(\hat{R}_{naive}(\hat{Y})\)关于示性矩阵\(O\)的期望为\(E_O[\hat{R}_{naive}(\hat{Y})]\)。可以看到\(E_O[\hat{R}_{naive}(\hat{Y})]!=R(\hat{Y})\)，说明\(E_O[\hat{R}_{naive}(\hat{Y})]\)只是\(R(\hat{Y})\)的有偏估计。为了达到无偏估计，论文采用逆倾向分数对数据进行加权，此时可构建一个对理想评价指标的无偏估计器IPS Estimator，最终得到的评测标准指标\(\hat{R}_{IPS}(\hat{Y}|P)\)表示如下：

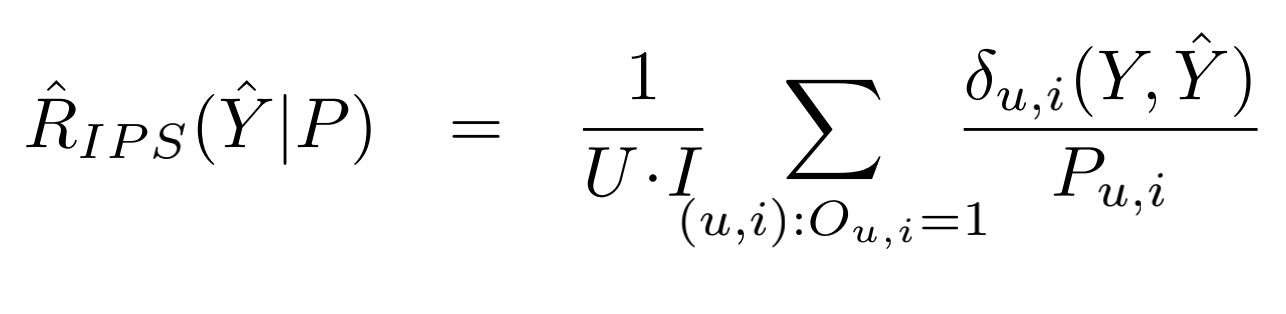
根据该论文所述，预测倾向分数可采用多种方法，如朴素贝叶斯、逻辑回归等。论文提出了一个基于倾向分数的矩阵分解模型（MF-IPS）用于推荐任务。分别在半合成的数据集和真实数据集上证明了IPSEstimator是对理想评测指标的无偏估计和MF-IPS模型效果优于传统的矩阵分解算法，达到了去除选择偏差的目的。

偏差和不公平————基于ML的推荐算法与生俱来的“原罪”

偏差和不公平可以说是基于ML的推荐算法与生俱来的“原罪”，他本质上就暗藏在数据中（没错，数据是会骗人的），随着机器学习算法的执行而加剧。
目前在公平性领域，人们提出了包括但不限于下面的五种不公平和偏差的来源。
人口平等 解决方案: ①使用对抗学习去除用户embeddings向量中的敏感信息；或者更近一步，通过正交性正则化。②使有偏差用户向量尽量正交于无偏差用户向量，从而使两者区分开来。
位置偏差 解决方案: 将其转换为一个以排序质量做为约束条件的整数线性规划(ILP)问题求解。
选择偏差 解决方案: 可以采用因果推断的角度，利用逆倾向分数 (IPS) 对观察数据进行加权，构建一个对理想评测指标的无偏估计器 (倾向分数可以看作是每个数据被观察到的概率)
曝光偏差 解决方案：同样可以采用因果推断的角度，给用户曝光商品可以看做给病人施加药物，只知道少数病人 (用户) 对少数治疗方式 (物品) 的反应。我们同样可以基于倾向分数方法，构建无偏估计器。
流行度偏差 解决方案：可以采用基于正则化的内处理 (In-processing) 方法，采用用户-物品对的预测分数和物品对应的流行度之间的皮尔逊相关系数作为正则项，通过最小化正则项和推荐误差来消除偏差。也可以采取因果推断的角度，分析得出物品流行度是曝光物品和交互之间的一个混淆因子，因此要消除流行度对物品曝光度的影响，但是须保留流行度对交互 (捕获用户的从众心理) 的影响，即利用流行度差。
总体而言，我们可以发现目前提出的结局公平性问题的方法非常多样化，反事实、因果推断、混淆因子等概念正在强势崛起。

偏差和不公平所产生的根本原因

前面我们说偏差和不公平本质上就暗藏在数据中，是因为在推荐系统中，由于用户行为数据是观察所得 (Observational) 而不是实验所得 (Experimental)，因此会存在各种偏差，如用户对物品的选择偏差、系统对物品的曝光偏差等，直接拿模型拟合数据而忽视偏差会导致性能欠佳，在一定程度上也损害了用户对推荐系统的体验和信任，因此，去除推荐系统偏差已经成为推荐系统领域研究的一个新方向。
而单纯基于ML的方法能彻底解决不公平问题吗？这是一个我们不得不讨论的问题。目前学术界采用的去除偏差的方法中，大多数还是在原有机器学习算法上进行一定修改，通过修改目标函数、添加优化算法约束、添加正则项等手段来达到去除偏差的目的。然而我们知道这些偏差本身就是ML算法所导致的，这样很难从本质上解决问题。

辛普森悖论

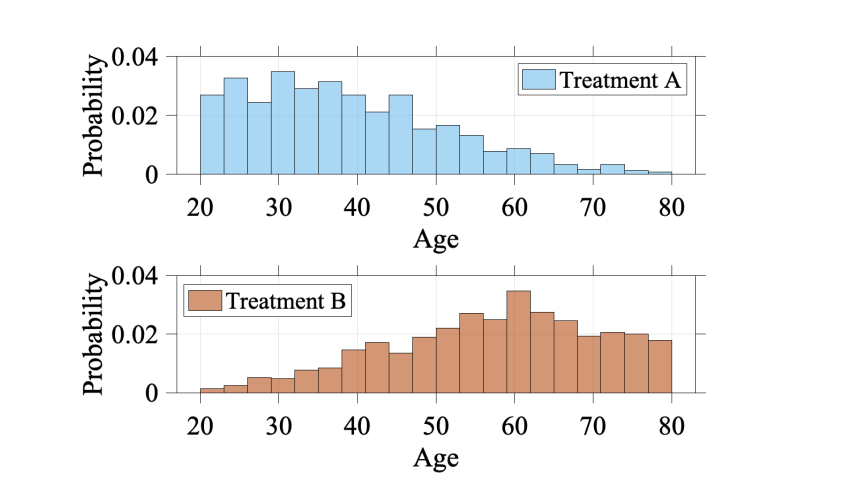
关于数据本身的偏差，有一个经典的辛普森悖论。这种现象可以体现为：在年轻和老年的病人群体中，药物B相比药物A都有着更高的痊愈率；但是当我们把这两个群体结合起来会发现，药物A的痊愈率会更高。如下图所示:

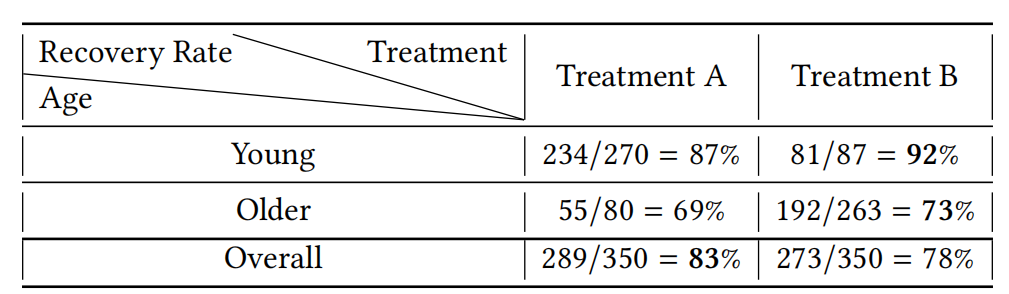
后面我们从因果推断的角度（Confounder）可以发现，悖论其实是由混淆因子导致的：当将所有群体一起比较时，大多数服用药物A的人非常年轻，所以表格展示的比较不能排除年龄(age)这一混淆因子对痊愈率的影响。如下图所示:

因果推理——通向智能的阶梯

图灵奖得主Judea Pearl曾在NIPS 2017上做过一个汇报，汇报的主题是《Theoretical impediments to machine learning with seven sparks from the causal revolution》，着重介绍了因果推理对于实现强人工智能的重要性。以下是汇报中阐述机器学习能力边界的一页PPT:

不过那个时候大家正忙着炼丹，这个报告也未能得到重视。不过现在随着因果推断在机器学习的各大领域得到了应用（包括了因果表征学习和这里在推荐系统公平性领域的应用），人们逐渐认识到了Pearl当初提出的几点看法的重要性。
Pearl的PPT中还有一页创新性地提出的智能的三个阶段，其中第一阶段是“关联”，也就是传统统计学中的相关性，具体体现为“如果观察到....，那么....”；第二阶段是“介入”，具体体现为“我做了....（进行干预)，那么....”；第三阶段为“反事实”，具体体现为“假如我做了...， 那么...”。这三个阶段如下图所示：

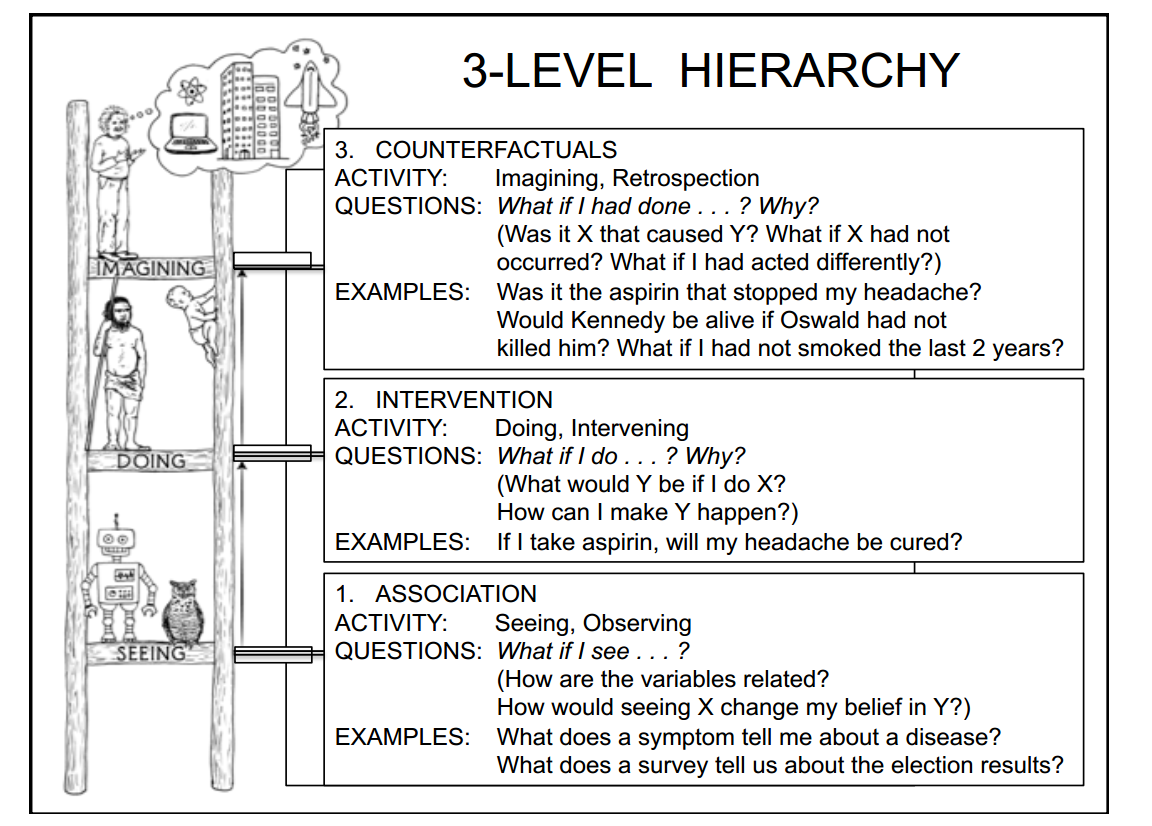
中基于机器学习方法的人工智能和普通动物在第一阶段，原始人类（认知革命前的）和婴儿在第二阶段，现代人类在第三阶段。可以看出，因果推理是通向智能的阶梯，而拥有“反事实”这一概念是人类进行认知革命的标志。
Pearl在这里引述了赫拉利在《人类简史》中关于“狮人”雕塑的论述，这个雕塑表现的是一个在客观世界不存在的事物，Pearl认为这个雕塑是人类最开始利用“反事实”进行推断的表现。

因果推断入门

下面简要介绍一下因果推断的重要概念。

(1) 三个步骤

一般而言，因果推断包括以下三个重要的步骤：预测(prediction)，介入(intervention)和反事实(counterfactuals)。我们以下面这个因果图为例：

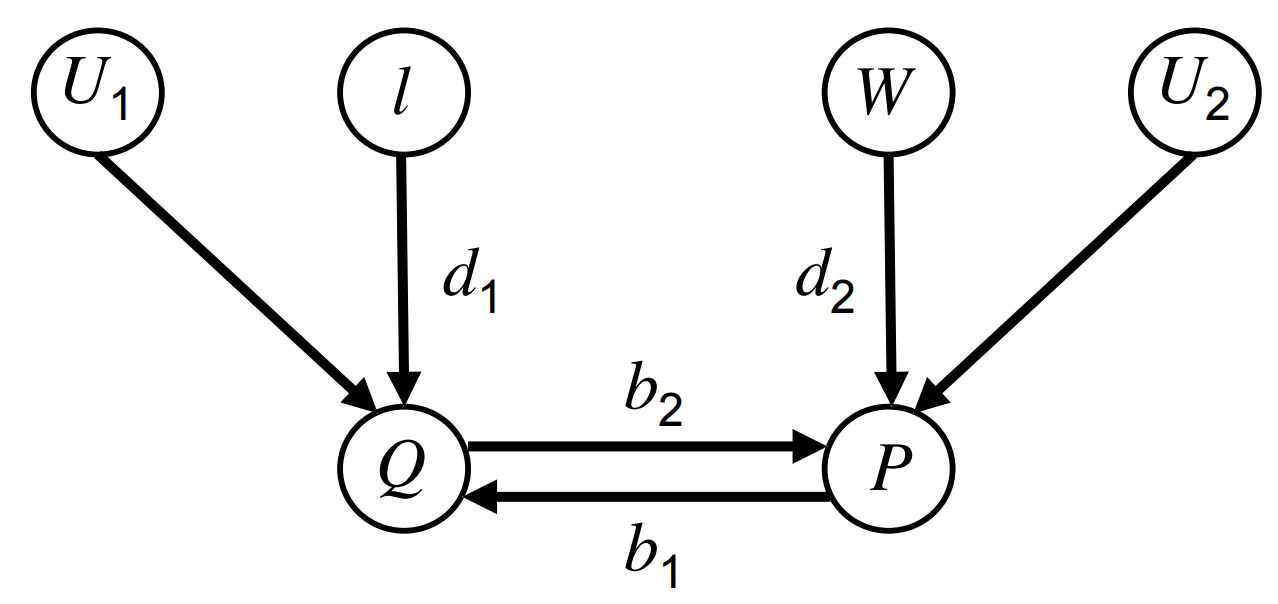
其中\(P\)表示价格(Price)，\(Q\)表示需求（Demand），\(I\)表示收入(Income)，\(W\)表示工资(Wages)。其中我们定义以下符号：

• 已知价格为\(P=p_0\)的情况下，需求\(Q\)的期望值：\(E[Q|P=p_0]\)
• 当价格被设定为\(P=p_0\)时，需求\(Q\)的期望值：\(E[Q|do(P=p_0)]\)
• 给定现阶段的价格\(P=p_0\)，如果我们将价格设定为\(P=p_1\)，需求\(Q\)的期望值：\(E[Q_P=p_1|P=p_0]\)

(2) 结构化因果模型(SCM)和因果关系之间的转换

上面我们提到的因果图为结构化因果模型(SCM)。SCM和因果关系之间可以相互转换^[3]。例如，下面(a)图对应的因果关系为\(z=f_Z(u_Z), x=f_X(z,u_X), y=f_Y(x,u_Y)\)，（b）图对应的因果关系为\(z=f_Z(u_Z), x=x_0, y=f_Y(x,u_Y)\)。这里\(U_Z，U_X，U_Y\)相互独立。

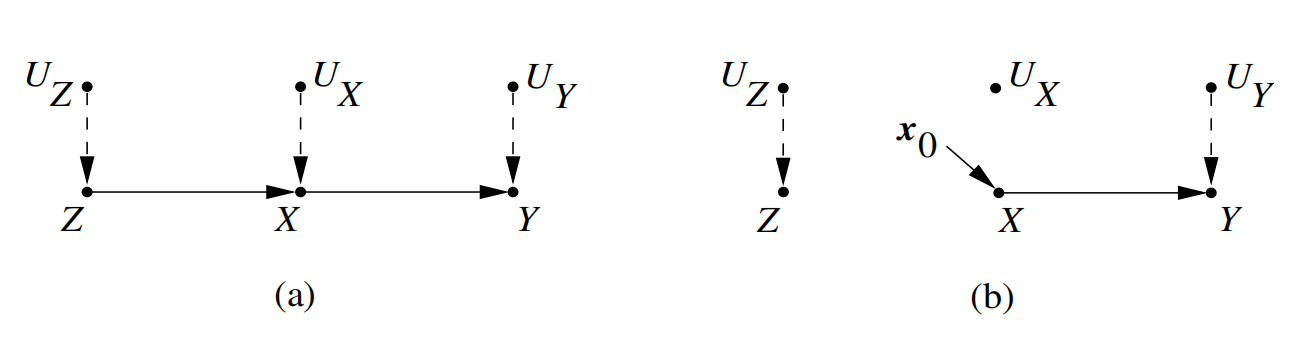
(3) 后门准则(back-door criterion)

我们已经知道了怎样用因果图来对因果关系进行建模，但最终我们仍然要落实到计算上。而计算的前提是我们需要将因果关系的概率表达式中的\(do\)算子消去。Pearl提出了后门准则（back-door criterion）^[4]，对于满足一定条件的因果图，可以将带\(do\)算子的概率表达式表示为不带\(do\)算子的概率表达式。接下来我们简要介绍一下后门准则。
在SCM中，如果一条无向连接X和Y的路径有一条指向X的箭头，我们把这条路径称为从X到Y的后门路径。如果后门路径存在，实际结果中可能出现虚假的统计相关性。
当一个变量集合S符合以下两个条件时，我们称S符合后门准则：

• S中不包括 X的后代。
• S能d分割所有从 X到Y的后门路径。
  在下图中，\(\{Z_1,Z_2,Z_3\}\),\(\{Z_1,Z_3\}\)等集合都满足后门准则，但\(\{Z_3\}\)不满足后门准则。

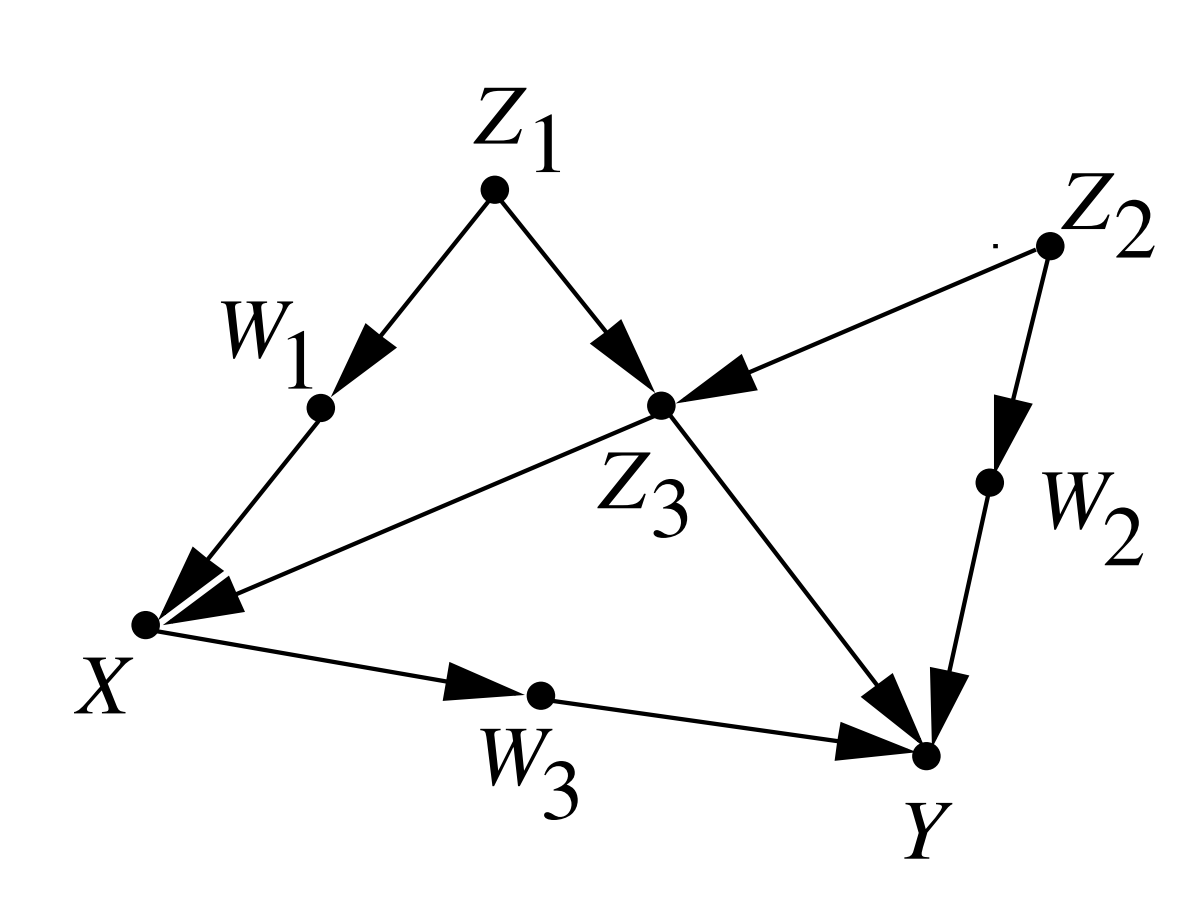
后门推导告诉我们，如果\(S\)满足从\(X\)到\(Y\)的后门准则，那么我们可以将\(do\)算子消去，得到概率表达的公式：

\[\begin{matrix} P(Y=y|do(X=x), S=s)=P(Y=y|X=x, S=s)\\ P(Y=y|do(X=x))=∑_sP(Y=y|X=x, S=s)P(S=s)= ∑_s \frac{P(Y=y, X=x, S=s)}{P(X=x, S=s)} \end{matrix} \]

去除混淆因子举例

因果推断还有一种典型应用是去除混淆因子。在论文《Causal Intervention for Leveraging Popularity Bias in
Recommendation》 ^[5] 中就应用了这种思想。该论文从因果推断的角度出发，分析得出物品流行度是曝光物品和交互 之间的一个混淆因子 (Confounder)，因此要消除流行度对物品曝光度的影响，但 是须保留流行度对交互 (捕获用户的从众心理) 的影响，即利用流行度偏差。具体流程如下图所示：

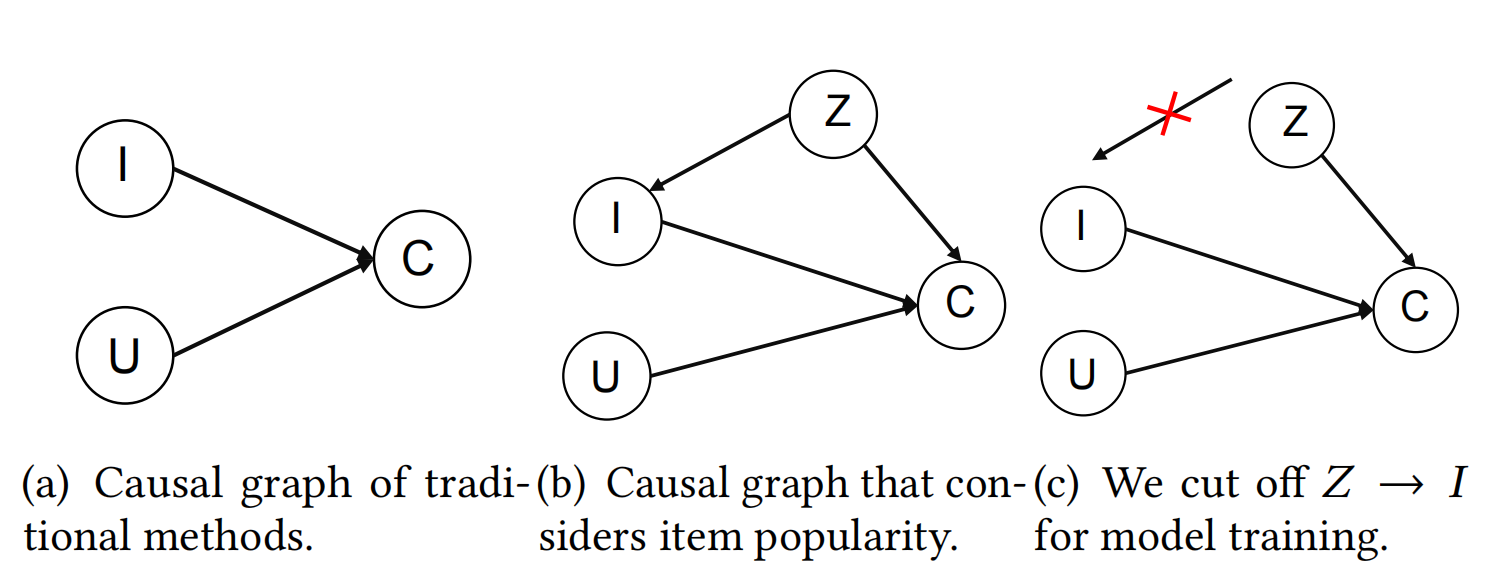
(其中\(I\)表示用户，\(U\)表示曝光物品，\(C\)表示交互概率，\(Z\)表示物品流行度。我们将\(Z\)定义为\(I\)和\(C\)之间的混淆因子，并在训练阶段消除混淆因子影响，采用\(P（C|do(U,I)）\)作为兴趣匹配)

研究计划

目前我初步确定了因果推断作为未来的研究方向，我拟定的研究计划如下：

1. 了解概率图模型知识 这方面可阅读 Koller D和Friedman N写的《Probabilistic graphical models: principles and techniques》^[6]。
2. 系统学习因果推断知识 这方面可阅读 Pearl J.写的《Causality》^[4]。
3. 阅读在推荐系统公平性中+因果推断的论文 这方面可关注顶会论文。ICML、SIGIR、WSDM、WWW等顶会近年来都有大量将因果推断与推荐系统的偏差/公平性相结合的论文。
4. 论文复现与实验 在论文复现过程中，可充分利用因果推断相关的开源库，比如dowhy^[7]、causal ML^[8]、EconML ^[9] 等。

开源库介绍

下面简要介绍一下因果推断的开源库及其特色。

(1) Dowhy

语言: Python
支持方法: 倾向回归分层&匹配、逆倾向加权、回归方法

(2) Causal ML

语言: Python
支持方法: 基于树的方法、元学习方法

(3) EconML

语言: Python
支持方法: 双重稳健估计器、正交随机森林、元学习方法、深度工具变量

(3) CausalToolbox

语言: R
支持方法: 贝叶斯可加回归树、因果森林、基于树的元学习器

参考文献

• [1] Schnabel T, Swaminathan A, Singh A, et al. Recommendations as treatments: Debiasing learning and
  evaluation[C]//international conference on machine learning. PMLR, 2016: 1670-1679.
• [2] Pearl J. Theoretical impediments to machine learning with seven sparks from the causal revolution[J].
  arXiv preprint arXiv:1801.04016, 2018.
• [3] Spirtes P. Introduction to causal inference[J]. Journal of Machine Learning Research, 2010, 11(5).
• [4] Pearl J. Causality[M]. Cambridge university press, 2009.
• [5] Zhang Y, Feng F, He X, et al. Causal Intervention for Leveraging Popularity Bias in
  Recommendation[J]. arXiv preprint arXiv:2105.06067, 2021.
• [6] Koller D, Friedman N. Probabilistic graphical models: principles and techniques[M]. MIT press, 2009.
• [7] https://microsoft.github.io/dowhy/
• [8] https://causalml.readthedocs.io/en/latest/about.html
• [9] https://econml.azurewebsites.net/

标签：公平性,偏差,新思路,用户,推断,物品,hat,因果
来源： https://www.cnblogs.com/lonelyprince7/p/15378912.html