CF213C

Description：

输入一个 \(n\times n\) 的矩形，每个 \(a_{i,j}\) 是这个位置的价值。现在要从左上角走到右下角再返回，每个价值只被计算一次，求最大价值和。

Solution:

对于一去一回，直接这么想的话太麻烦了，可以想象成两条去的路径，因为取值都是一样的。

相当于是这么两条路径。

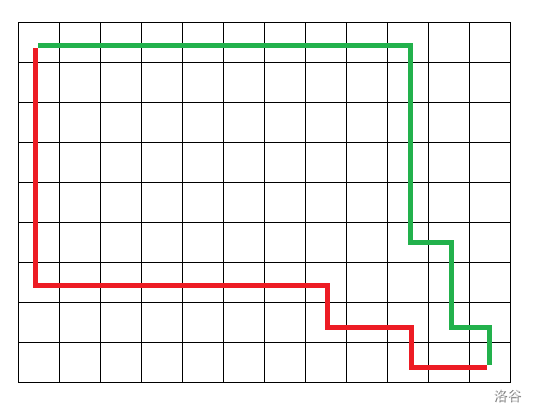
很显然，可以写个四维 dp，设 \(f_{x_1,y_1,x_2,y_2}\) 表示第一个人在 \((x_1,y_1)\) ，第二个人在 \((x_2,y_2)\) 时可以取到的最大值。但是 \(1\leq n\leq 300\) ，开四维直接起飞。考虑精简状态。

设 \(f_{i,j,k}\) 表示当前走了 \(i\) 步，路线一在 \(j\) 行，路线二在 \(k\) 行，所能得到的最大值。

考虑状态转移，我们既然已经知道了当前走的步数，也知道了当前在第几行，每次又只能走一格，我们用走的步数减去当前的行数不就是我们当前的列数吗。

我们在考虑当前点可能是从哪里来的。可以向下走，也可以向右走，如果行没变，就相当于向右走了，变了，就是向下走了，因此可以从下图的几个方向转移而来。

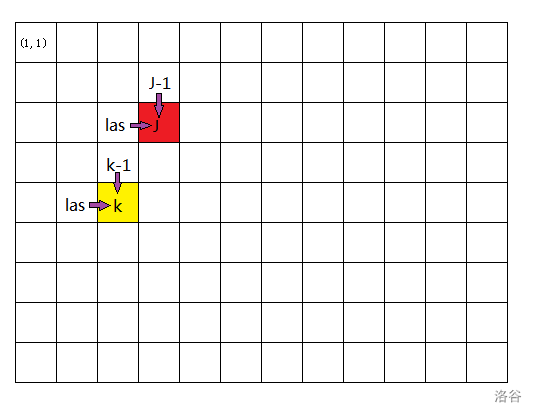
然后将这四个可能组合一下，就可以得出我们的状态转移方程：

\[\begin{cases} f_{i,j,k}=\min(f_{i,j,k},f_{i-1,j,k}+a_{j,i-j+1}+a_{k,i-k+1}(j\not= k)) \\ f_{i,j,k}=\min(f_{i,j,k},f_{i-1,j-1,k}+a_{j,i-j+1}+a_{k,i-k+1}(j\not= k)) \\ f_{i,j,k}=\min(f_{i,j,k},f_{i-1,j,k-1}+a_{j,i-j+1}+a_{k,i-k+1}(j\not= k)) \\ f_{i,j,k}=\min(f_{i,j,k},f_{i-1,j-1,k-1}+a_{j,i-j+1}+a_{k,i-k+1}(j\not= k)) \end{cases} \]

初始化： \(f_{1,1,1}=a_{1,1}\)

答案: \(f_{2\times n-1,n,n}\)

为什么是 \(2\times n-1\)，仔细算一下，其实我们走了 \(2\times n-1\) 步。我不会告诉你我第一次写成了 \(2\times n\)

Code

#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
using namespace std;
const int mod=998244353;
const int M=3e2+5;
int f[2*M][M][M],n,mp[M][M];
int read()
{
	int x=0,y=1;
	char c=getchar();
	while(c<'0' || c>'9') {if(c=='-') y=0;c=getchar();}
	while(c>='0' && c<='9') { x=x*10+(c^48);c=getchar();}
	return y?x:-x;
}
int main()
{
	n=read();
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			mp[i][j]=read();
	f[1][1][1]=mp[1][1];//第一个位置
	for(int i=2;i<=2*n;i++)
		for(int j=1;j<=n;j++)
			for(int k=1;k<=n;k++)
			{
				f[i][j][k]=max(f[i][j][k],f[i-1][j][k]+mp[j][i-j+1]+(j!=k)*mp[k][i-k+1]);
				f[i][j][k]=max(f[i][j][k],f[i-1][j-1][k]+mp[j][i-j+1]+(j!=k)*mp[k][i-k+1]);
				f[i][j][k]=max(f[i][j][k],f[i-1][j][k-1]+mp[j][i-j+1]+(j!=k)*mp[k][i-k+1]);
				f[i][j][k]=max(f[i][j][k],f[i-1][j-1][k-1]+mp[j][i-j+1]+(j!=k)*mp[k][i-k+1]);
			}
	printf("%d\n",f[2*n-1][n][n]);
	return 0;
}

标签：CF213C,min,int,题解,可以,times,向右走,当前
来源： https://www.cnblogs.com/jcgf/p/15245322.html