首页 > 其他分享> > 多源最短路多种实现方式

多源最短路多种实现方式

2021-09-05 16:01:36 作者：互联网

问题引入

以下代码均对应本题

Floyd算法

时间复杂度
\(O(n^3)\)

特点

仅适用于数据范围较小的情况
既适用于图，也适用于树

算法流程
Floyd算法

倍增借助LCA

时间复杂度
预处理：\(O(nlog_n)\)
单次查询: \(O(log_n)\)

实现流程

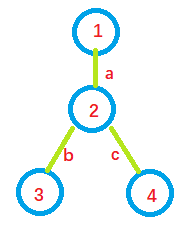
目标求解\(3\)，\(4\)两点间最短距离\(dis\)，有两种求解方式

\(dis = b + c\)
借鉴\(f[i][k]\)的思想，预处理\(dis[i][k]\)，即从i点走\(2^k\)步所涉及到的所有边中边权最小值
根据\(dis[i][k]\)，即可在求lca的同时分别计算出a，b到p的最短距离
求和即为答案

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <queue>

using namespace std;

const int N = 1e4 + 10, M = N * 2;

int n, m;
int h[N], e[M], ne[M], w[M], idx;
int depth[N], f[N][14], dis[N][14];
queue<int> q;

void add(int a, int b, int c)
{
    e[idx] = b;
    ne[idx] = h[a];
    w[idx] = c;
    h[a] = idx ++;
}
void bfs(int root)
{
    memset(depth, 0x3f, sizeof depth);
    q.push(root);
    depth[0] = 0;
    depth[root] = 1;

    while (q.size())
    {
        int t = q.front();
        q.pop();

        for (int i = h[t]; ~i; i = ne[i])
        {
            int p = e[i];
            if (depth[p] == 0x3f3f3f3f)
            {
                q.push(p);

                depth[p] = depth[t] + 1;

                dis[p][0] = w[i];
                f[p][0] = t;
                for (int k = 1; k <= 13; ++ k)
                {
                    f[p][k] = f[f[p][k - 1]][k - 1];
                    dis[p][k] = dis[p][k - 1] + dis[f[p][k - 1]][k - 1];
                }
            }
        }
    }
}
int get_dis(int a, int b)
{
    int res = 0;
    if (depth[a] < depth[b]) swap(a, b);
    for (int k = 13; ~k; -- k)
        if (depth[f[a][k]] >= depth[b])
        {
            res += dis[a][k];
            a = f[a][k];
        }
    if (a == b) return res;
    for (int k = 13; ~k; -- k)
        if (f[a][k] != f[b][k])
        {
            res += dis[a][k] + dis[b][k];
            a = f[a][k];
            b = f[b][k];
        }
    res += dis[a][0] + dis[b][0];

    return res;
}
int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m;
    while (-- n)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }

    bfs(1);

    while (m --)
    {
        int a, b;
        cin >> a >> b;
        cout << get_dis(a, b) << endl;
    }

    return 0;

\(dis = (b + a) + (c + a) - 2 * a\)
在预处理原有求lca的数据以外，再预处理出各点距离根节点的路径长度dis[i](DFS / BFS 均可)
对于一次查询(a, b), 答案为 \(dis[a] + dis[b] - 2 * dis[lca(a, b)]\)

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <queue>

using namespace std;

const int N = 1e4 + 10, M = N * 2;

int n, m;
int h[N], e[M], ne[M], w[M], idx;
int depth[N], f[N][14], dis[N];
queue<int> q;

void add(int a, int b, int c)
{
    e[idx] = b;
    ne[idx] = h[a];
    w[idx] = c;
    h[a] = idx ++;
}
void bfs(int root)
{
    memset(depth, 0x3f, sizeof depth);
    q.push(root);
    depth[0] = 0;
    depth[root] = 1;

    while (q.size())
    {
        int t = q.front();
        q.pop();

        for (int i = h[t]; ~i; i = ne[i])
        {
            int p = e[i];
            if (depth[p] == 0x3f3f3f3f)
            {
                q.push(p);

                depth[p] = depth[t] + 1;
                dis[p] = dis[t] + w[i];

                f[p][0] = t;
                for (int k = 1; k <= 13; ++ k)
                    f[p][k] = f[f[p][k - 1]][k - 1];
            }
        }
    }
}
int lca(int a, int b)
{
    if (depth[a] < depth[b]) swap(a, b);
    for (int k = 13; ~k; -- k)
        if (depth[f[a][k]] >= depth[b])
            a = f[a][k];
    if (a == b) return a;
    for (int k = 13; ~k; -- k)
        if (f[a][k] != f[b][k])
        {
            a = f[a][k];
            b = f[b][k];
        }
    return f[a][0];
}
int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m;
    while (-- n)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }

    bfs(1);

    while (m --)
    {
        int a, b;
        cin >> a >> b;
        int p = lca(a, b);
        if (p == a) cout << (dis[b] - dis[a]) << endl;
        else if (p == b) cout << (dis[a] - dis[b]) << endl;
        else cout << (dis[a] - 1) + (dis[b] - 1) - 2 * (dis[p] - 1) << endl;
    }

    return 0;
}

Tarjan算法

时间复杂度
\(O(n)\)
倍增LCA虽然查询为\(O(log_n)\)，但是由于存在\(O(nlog_n)\)的预处理，所以算法整体性能为\(O(nlog_n)\)
而Tarjan采用并查集，能够将查询复杂度降低为\(O(1)\)，需要遍历到所有点，所以算法整体性能为\(O(n)\)

特点

属于离线做法
比倍增LCA代码难写且难以理解

算法流程
距离采用的是\(dis = (b + a) + (c + a) - 2 * a\)
与倍增LCA相比，不同点在于求最近公共祖先的方法。

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <queue>
#include <vector>

using namespace std;
using PII = pair<int, int>;

const int N = 1e4 + 10, M = N * 2;

int n, m;
int h[N], e[M], ne[M], w[M], idx;
int p[N];
queue<int> q;
int res[M];
int st[N];
int dis[N];
vector<PII> query[M];

int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}
void add(int a, int b, int c)
{
    e[idx] = b;
    ne[idx] = h[a];
    w[idx] = c;
    h[a] = idx ++;
}
void bfs(int root)
{
    memset(dis, 0x3f, sizeof dis);
    dis[root] = 0;
    q.push(root);

    while (q.size())
    {
        int t = q.front();
        q.pop();

        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];
            if (dis[j] == 0x3f3f3f3f)
            {
                dis[j] = dis[t] + w[i];
                q.push(j);
            }
        }
    }
}
/**
 * tarjan难在回溯
 * 很多操作之间都存在严格的先后关系，由于结合递归回溯，难理解很多
 */
void tarjan(int x)
{
    st[x] = 1; // 搜索开始
    // 遍历u节点下的所有子节点
    for (int i = h[x]; ~i; i = ne[i])
    {
        int j = e[i];
        if (!st[j]) // st = 0表示不是正在搜索且不是已经搜索完成，是还未搜索
        {
            tarjan(j);
            p[j] = x;
        }
    }

    for (auto question : query[x])
    {
        int y = question.first, id = question.second;
        if (st[y] == 2)
        {
            int ancestor = find(y);
            /**
             * find(y)为什么是最近公共祖先？
             * 这个和tarjan(j)，p[j] = x的先后顺序有关，只有在把以x节点为根节点的子树全部搜索完成后，
             * x节点的p[x]才会更新会上层节点，所以x节点以下的节点所找到的父节点都是x而非整棵树的根节点
             * 比较适合理解这个问题的例子
             *         a
             *         |
             *         b
             *        / \
             *       c   d
             * 询问(c, d)距离
             * tarjan(a) -> tarjan(b) -> tarjan(c), p[c] = b; tarjan(d)
             * p[a] = a     p[b] = b      p[c] = b
             * 因为在d那一层计算(c，d)距离时，p[b] = b并没有更新，但c点的tarjan已经结束
             * 所以p[c]已经更新为b，所以find(c) = b，是c与d的最近公共祖先，而非根节点a
             */
            res[id] = dis[x] + dis[y] - 2 * dis[ancestor];
        }
    }

    st[x] = 2; // 搜索完成
}
int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for (int i = 0; i < n - 1; ++ i)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }

    for (int i = 0; i < m; ++ i)
    {
        int a, b;
        cin >> a >> b;
        /**
         * 存储了2次
         * 答案存储依据的是问题编号i，所以多存储并不会影响最终结果
         * 需要存储2次的原因是距离的计算只有在回溯的时候可以计算出来
         * 我们无法确定点与点之间的位置关系，所以需要存储2次数
         */
        query[a].push_back({b, i});
        query[b].push_back({a, i});
    }

    for (int i = 1; i <= n; ++ i) p[i] = i;

    bfs(1); // 初始化各节点距离根节点距离
    tarjan(1);

    for (int i = 0; i < m; ++i) cout << res[i] << endl;

    return 0;
}

标签：多种,idx,int,短路,ne,depth,include,多源,dis
来源： https://www.cnblogs.com/G-H-Y/p/15229629.html