AT4778 [ABC130F] Minimum Bounding Box
作者:互联网
题解
定义函数 \(f_x(t)=x_{\max}-x_{\min},\ \ f_y(t)=y_{\max}-y_{\min}\),可以它们是分段函数(或常函数),且值域 \(\subseteq[0,+\infty]\)。
设 \(f_x(t)\times f_y(t)\) 在 \(t_0\) 处取得最小值。
若 \(t_0\) 不是函数 \(f_x,f_y\) 中任意一个的转折点,则可得
\([f_x(t_0)\times f_y(t_0)]'=0\),即 \(f_x'(t_0)\times f_y(t_0)+f_x(t_0)\times f_y'(t_0)=0\),所以有:
- \(f_x'(t_0)\) 与 \(f_y'(t_0)\) 中有且仅有一个为负。
或者:
- 这四项中,前两项、后两项分别有至少一项为 \(0\)。
对于 \((1)\),设 \(f_x'(t_0)< 0\),则取充分小的 \(\epsilon\) 总能使 \([f_x(t_0+\epsilon)\times f_y(t_0+\epsilon)]'<0\),则 \(f_x(t_0+\epsilon)\times f_y(t_0+\epsilon)\) 更小,矛盾。
对于 \((2)\),进行分类讨论即可,在这里不再赘述。
最终可得 \(t_0\) 必定是函数 \(f_x,f_y\) 中至少一个的转折点。
实现
由上文得,我们分别找到 \(f_x,f_y\) 的转折点 \(t_0,t_1,\cdots\),依次代入即可。
在 \(x\) 轴正方向上,只有 \(x\) 最大的 L 点,\(x\) 最大的 R 点和 \(x\) 最大的 U/D 点两两相遇时,此时的 \(t\) 才可能成为 \(f_x\) 的转折点,对于另外三个方向同理。
所以 \(O(n)\) 扫一遍处理出这些特殊点,然后逐个检验 \(t\) 即可。
#include<bits/stdc++.h>
using namespace std;
int qread(){
int tmp=0;char buf=getchar();bool f=true;
while(!isdigit(buf)){if(buf=='-')f=false;buf=getchar();}
while(isdigit(buf)){tmp=tmp*10+buf-'0';buf=getchar();}
return f?tmp:-tmp;
}
int getdir(){
char c=getchar();
while(!isupper(c))c=getchar();
if(c=='R')return 0;
if(c=='L')return 1;
if(c=='U')return 2;
if(c=='D')return 3;
return 0x7f;
}
const int INF=1000000007;
int pol[4][2]={{-INF,INF},{INF,-INF},{-INF,INF},{INF,-INF}};
// R/L/U/D further/nearer
int stat[2][2]={{INF,-INF},{-INF,INF}};
// moving in U/D or L/R, the Lst/Rst / Ust/Dst
double getarea(double t){
double Rst=max({stat[0][1]*1.0,pol[1][1]-t,pol[0][0]+t});
double Lst=min({stat[0][0]*1.0,pol[1][0]-t,pol[0][1]+t});
double Ust=max({stat[1][0]*1.0,pol[3][1]-t,pol[2][0]+t});
double Dst=min({stat[1][1]*1.0,pol[3][0]-t,pol[2][1]+t});
double ans=(Rst-Lst)*(Ust-Dst);
return ans;
}
double colls(int dir,int use){
double ans=0;
if(dir==0){
if(use==1)ans=max(ans,pol[1][1]-stat[0][1]*1.0);
if(use==2)ans=max(ans,stat[0][1]-pol[0][0]*1.0);
if(use==3)ans=max(ans,(pol[1][1]-pol[0][0])/2.0);
}else if(dir==1){
if(use==1)ans=max(ans,pol[1][0]-stat[0][0]*1.0);
if(use==2)ans=max(ans,stat[0][0]-pol[0][1]*1.0);
if(use==3)ans=max(ans,(pol[1][0]-pol[0][1])/2.0);
}else if(dir==2){
if(use==1)ans=max(ans,pol[3][1]-stat[1][0]*1.0);
if(use==2)ans=max(ans,stat[1][0]-pol[2][0]*1.0);
if(use==3)ans=max(ans,(pol[3][1]-pol[2][0])/2.0);
}else{
if(use==1)ans=max(ans,pol[3][0]-stat[1][1]*1.0);
if(use==2)ans=max(ans,stat[1][1]-pol[2][1]*1.0);
if(use==3)ans=max(ans,(pol[3][0]-pol[2][1])/2.0);
}
return ans;
}
int main(){
int n=qread();
for(int i=1;i<=n;i++){
int x=qread(),y=qread();
int dir=getdir();
if(dir==0){
pol[0][0]=max(pol[0][0],x);
pol[0][1]=min(pol[0][1],x);
}else if(dir==1){
pol[1][0]=min(pol[1][0],x);
pol[1][1]=max(pol[1][1],x);
}else if(dir==2){
pol[2][0]=max(pol[2][0],y);
pol[2][1]=min(pol[2][1],y);
}else{
pol[3][0]=min(pol[3][0],y);
pol[3][1]=max(pol[3][1],y);
}
if(dir<=1){
stat[1][0]=max(stat[1][0],y);
stat[1][1]=min(stat[1][1],y);
}else{
stat[0][0]=min(stat[0][0],x);
stat[0][1]=max(stat[0][1],x);
}
}
double area=1e24;
for(int i=0;i<=3;i++){
area=min(area,getarea(colls(i,1)));
area=min(area,getarea(colls(i,3)));
area=min(area,getarea(colls(i,2)));
}
area=max(area,0.0);
if(area-floor(area)>=0.38&&area-floor(area)<=0.62)cout<<fixed<<setprecision(0)<<floor(area)<<".50"<<endl;
else if(area-floor(area)>=0.13&&area-floor(area)<=0.37)cout<<fixed<<setprecision(0)<<floor(area)<<".25"<<endl;
else if(area-floor(area)>=0.63&&area-floor(area)<=0.87)cout<<fixed<<setprecision(0)<<floor(area)<<".75"<<endl;
else cout<<fixed<<setprecision(0)<<area<<".00"<<endl;
}
题外话:如何 hack 掉一部分三分的做法
设 \(f(t)\) 为时间 \(t\) 时的 \((x_{\max}-x_{\min})\times(y_{\max}-y_{\min})\),先假设 \(t\in[ 0, R ]\)。
考虑诱骗三分找到局部极值点 \(t_{local}\),则可以构造数据使得 \(t=0\) 时取得极小值,\(t=t_{local}\) 时取得次小值,且三分过程中左端点至少右移一次。
画图可以发现,若使 \(x_{\max}-x_{\min}\) 和 \(y_{\max}-y_{\min}\) 分别取得最小值的 \(t_x,t_y\) 相差很大,且这两个最小值都很小,则 \(f(t)\approx k(t-t_x)(t_y-t)\ \ (t_x\le t\le t_y,k\in[1,2,4])\)。
有了这个近似表示,可以考虑令其对称轴恰好落在某次三分区间中点的左侧不远处,则我们可以得到构造 hack 的步骤:
- 若三分右端点 \(R\geq10^8\),则将其乘 \((\dfrac{2}{3})^p\),得到新的右端点 \(R'\le 10^8\)。
- 取点 \((2,1)\),并使其向上移动。
- 取合适的小整数 \(\epsilon\) 使 \(R'\gg\epsilon\),加入点 \((R'-\epsilon,0),(-R'+\epsilon,0)\),并使其向原点移动。
易知,此时有局部极值点 \(t_{local}=R'-\epsilon\),此时 \(f(t_{local})=2(R'-\epsilon+1)\),而 \(f(0)=2(R'-\epsilon)\)。
若三分取点不同,设每次剩余的区间比例为 \(r\),则将第 1 步的 \((\dfrac{2}{3})^p\) 改为 \(r^p\) 即可。
使用例:
\(R=10^{10}\),此时我们得到 \(R'=10149592\),取 \(\epsilon=92\),则可以构造以下 hack 数据:
3
2 1 U
10149500 0 L
-10149500 0 R
正确输出为 20299000。
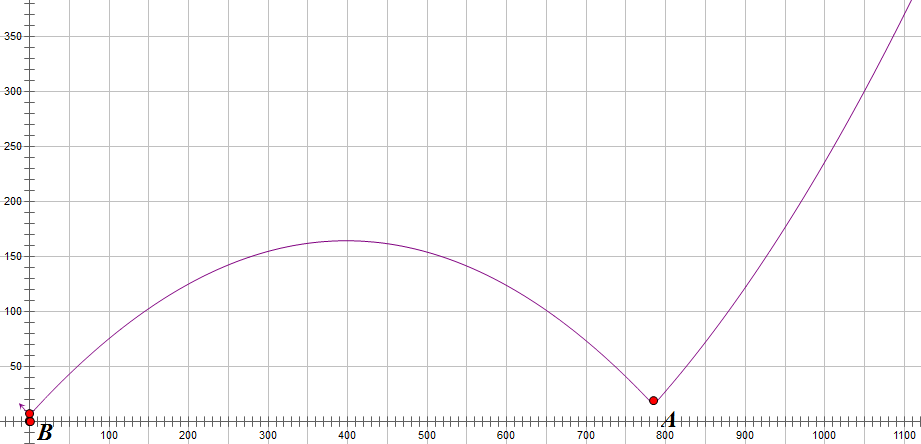
图像
这里有一个 hack 对应的 \(t\) - \(f(t)\) 图像,横轴为 \(t\)。
为了便于观察,图像进行了缩放,所以坐标轴上的数字没有实际意义。
标签:use,max,stat,ABC130F,pol,Minimum,ans,Bounding,INF 来源: https://www.cnblogs.com/XiEn1847/p/15101580.html