其他分享
首页 > 其他分享> > 图片滤波

图片滤波

作者：互联网

图片滤波

什么是滤波

滤波是将信号中特定波段频率滤除的操作，是抑制和防止干扰的一项重要措施。是根据观察某一随机过程的结果，对另一与之有关的随机过程进行估计的概率理论与方法。

图片和波如何结合

在不考虑透明度的情况下，图片可以由rgb构成，如果把rgb单独抽出来，可以得到3组由(0-255)构成的数组。再把这3组数组在坐标系中显示的话，可以得到3条连续的线。通过观察线的频率，可以看出图片颜色的平滑度。如果线段斜率越小说明该线段内的颜色越平滑，反之则反差越大。

如何滤波

方法一：使用AudioContext

滤波这种术语，一般会用在音频处理上，通过修改音频的频率从而达到修改声音的表现。例如AudioContext就有提供滤波函数createBiquadFilter ，其内部提供了一系列的滤波算法，例如高通滤波highpass ，低通滤波lowpass 。所以我们可以利用它的api去处理图片。

图1
图2
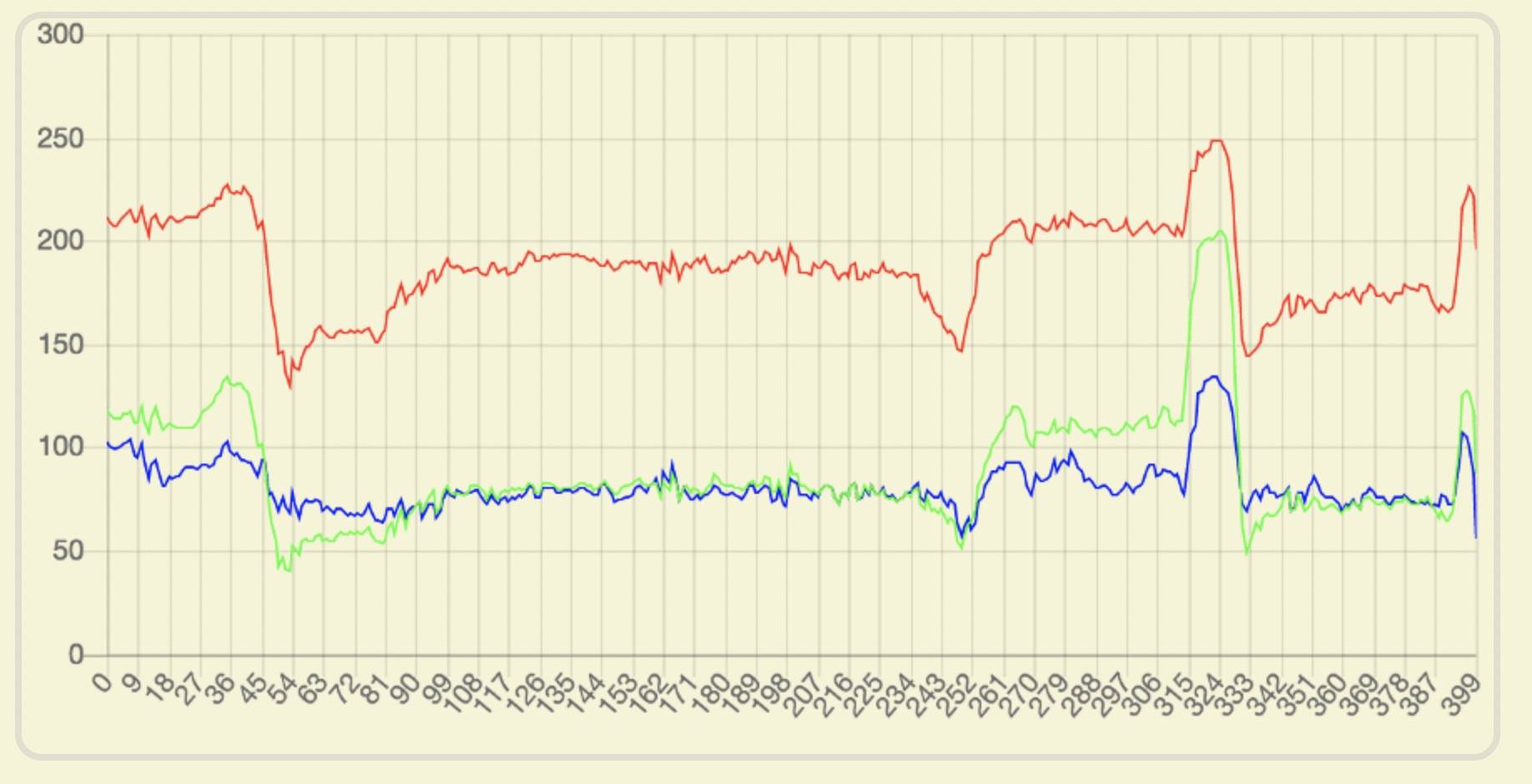
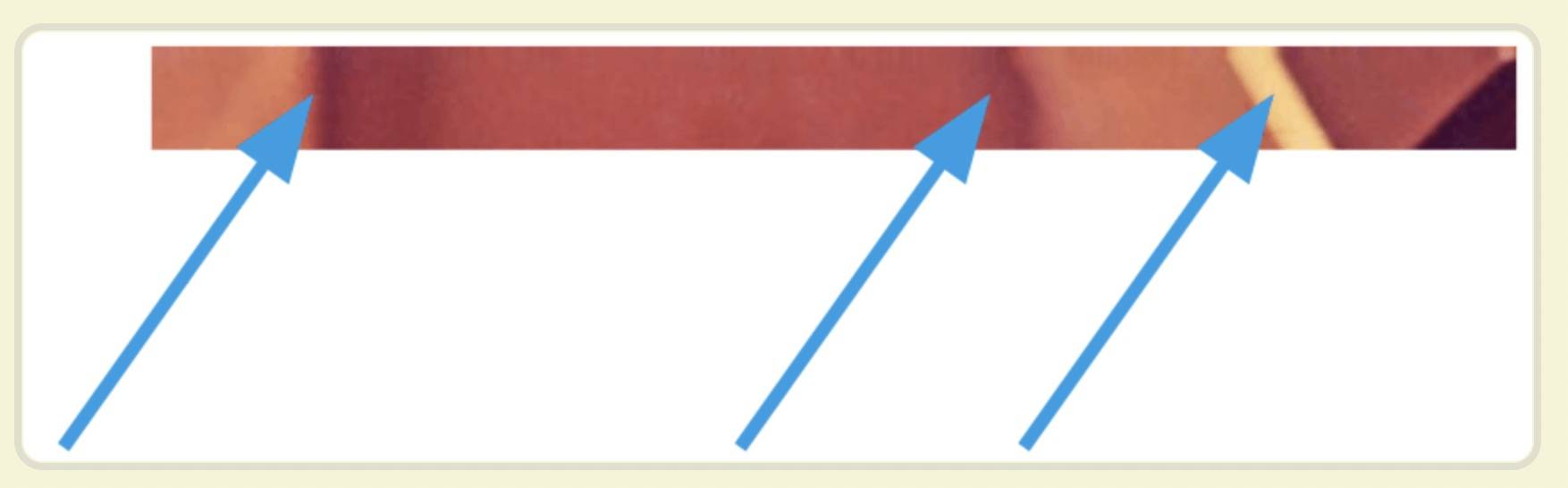
上图出处：图像与滤波

从上图可以看出曲线波动的地方就是图片边缘处，色差越大，波动越大。

方法二：通过卷积算法

什么是卷积

这里对卷积的理解有点抽象，所以直接跳过

卷积应用于图片

定义

用一个模板和一幅图像进行卷积，对于图像上的一个点，让模板的原点和该点重合，然后模板上的点和图像上对应的点相乘，然后各点的积相加，就得到了该点的卷积值。对图像上的每个点都这样处理。由于大多数模板都是对称的，所以模板不旋转。卷积是一种积分运算，用来求两个曲线重叠区域面积。可以看作加权求和，可以用来消除噪声、特征增强。

卷积运算图

卷积运算图
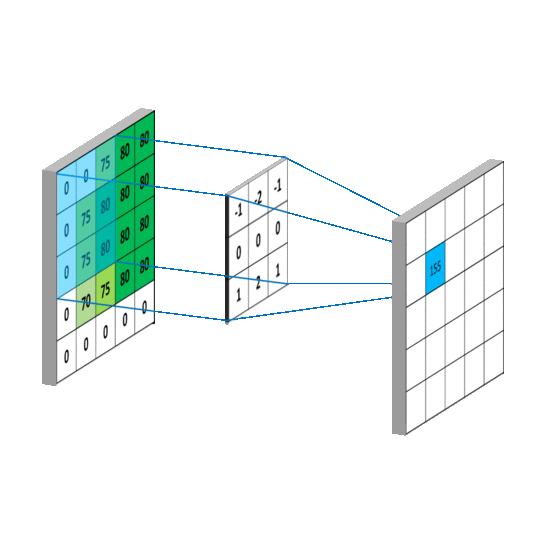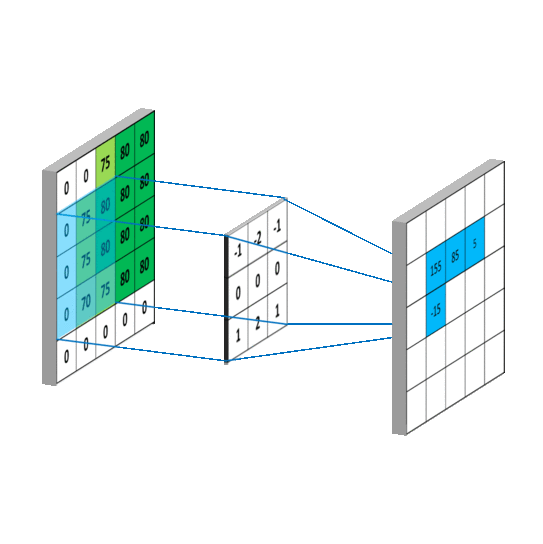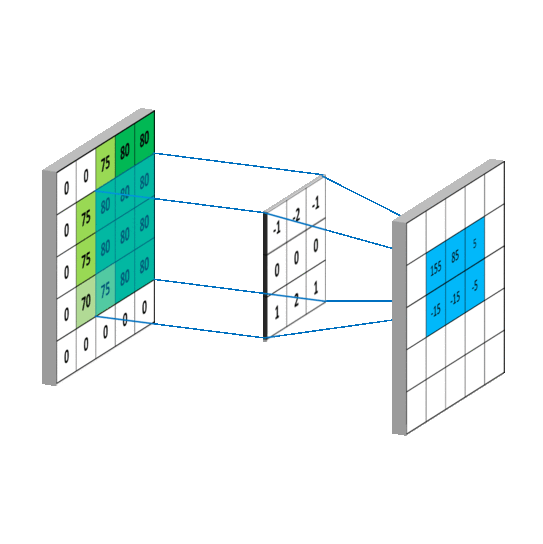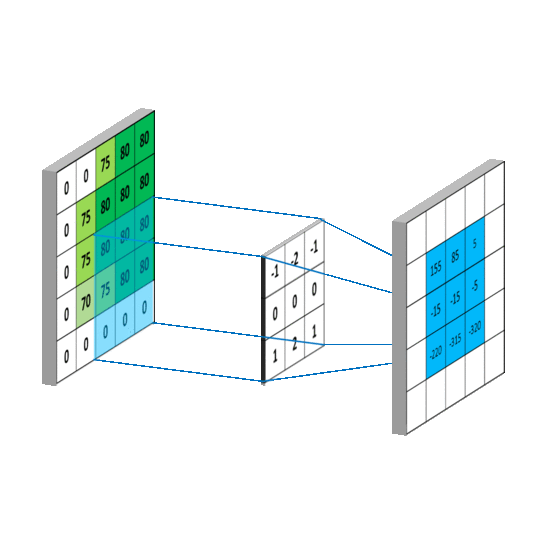
此图出处：onvolutional Neural Networks - Basics

卷积运算图-图2
此图出处：如何理解卷积
通过上面两张图中，中间层的是卷积核(模版)，可以看出其计算规则。而不同的滤波方式有对应的卷积核。
其实不难看出每个像素点的卷积计算其实都是和自身周围的像素进行计算而得到新的像素值。

卷积核

卷积核一般为奇数宽高的矩阵，一般为33，55。矩阵越大计算量越大

对应算法实现

function convolution (pixels:ImageData, weights:number[]) {
  const side = Math.round(Math.sqrt(weights.length))
  const halfSide = Math.floor(side / 2)
  const src = pixels.data
  const canvasWidth = pixels.width
  const canvasHeight = pixels.height
  const temporaryCanvas = document.createElement('canvas')
  const temporaryCtx = temporaryCanvas.getContext('2d')!
  const outputData = temporaryCtx.createImageData(canvasWidth, canvasHeight)

  for (let y = 0; y < canvasHeight; y++) {
    for (let x = 0; x < canvasWidth; x++) {
      const dstOff = (y * canvasWidth + x) * 4
      let sumReds = 0
      let sumGreens = 0
      let sumBlues = 0

      for (let kernelY = 0; kernelY < side; kernelY++) {
        for (let kernelX = 0; kernelX < side; kernelX++) {
          const currentKernelY = y + kernelY - halfSide
          const currentKernelX = x + kernelX - halfSide

          if (currentKernelY >= 0 &&
              currentKernelY < canvasHeight &&
              currentKernelX >= 0 &&
              currentKernelX < canvasWidth) {
            const offset = (currentKernelY * canvasWidth + currentKernelX) * 4
            const weight = weights[kernelY * side + kernelX]

            sumReds += src[offset] * weight
            sumGreens += src[offset + 1] * weight
            sumBlues += src[offset + 2] * weight
          }
        }
      }

      outputData.data[dstOff] = sumReds
      outputData.data[dstOff + 1] = sumGreens
      outputData.data[dstOff + 2] = sumBlues
      outputData.data[dstOff + 3] = 255
    }
  }
  return outputData
}

低通滤波

低通滤波去掉了高频信息，即细节信息，留下的低频信息代表了概貌。常用的例子，比如美图秀秀的磨皮，去掉了脸部细节信息（痘坑，痘印，暗斑等）。

高通滤波

高通滤波会过滤低频信息，保留高频信息。上面我们说过斜率越高说明颜色差异越大这里往往是图片边缘部分，也表示频率越高。所以只保留高频信号的话，说明只保留了图片的边缘部分。所以高通滤波往往用做边缘处理。

不同的滤波对应卷积核

均值滤波（加权平均模糊）
const weights = [
	1/9, 1/9, 1/9,
	1/9, 1/9, 1/9,
	1/9, 1/9, 1/9,
]

从上面的卷积核可以看出该卷积核的值之和为1，所以的目标是将目标像素点的值取周围的平均数，所以用该卷积核处理图片的结果会是模糊该图片，不过因为使用的是均值，所以图片不会很自然。一般使用高斯模糊滤波用作处理图片模糊。

高斯滤波

高斯模糊就是在均值滤波的基础上使用正态分布，通俗讲就是9宫格内的数值之和还是1，不过它们不是简单的均分了而是具有权重。越靠近中心的值会越大，所以高斯模糊相对均值模糊会和原图更加贴切。

正态分布的二维函数如下图：
二维正态分布

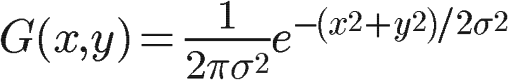
根据上面的公式可推导出的高斯矩阵方法：

function createGaussWeights (radius:number, sigma:number) {
  const gaussMatrix = []
  let gaussSum = 0
  radius = Math.floor(radius) || 3
  sigma = sigma || radius / 3
  const a = 1 / 2 * Math.PI * (sigma ** 2)
  const b = -1 / (2 * (sigma ** 2))
  let i = 0
  // 生成高斯矩阵
  for (let y = radius; y >= -radius; y--) {
    for (let x = -radius; x <= radius; x++) {
      const g = a * Math.exp(b * (x ** 2 + y ** 2))
      gaussMatrix[i++] = g
      gaussSum += g
    }
  }
  // 归一化
  for (let i = 0, len = gaussMatrix.length; i < len; i++) {
    gaussMatrix[i] /= gaussSum
  }
  return gaussMatrix
}

下图是3*3，模糊半径1.5的高斯模糊矩阵
高斯模糊矩阵

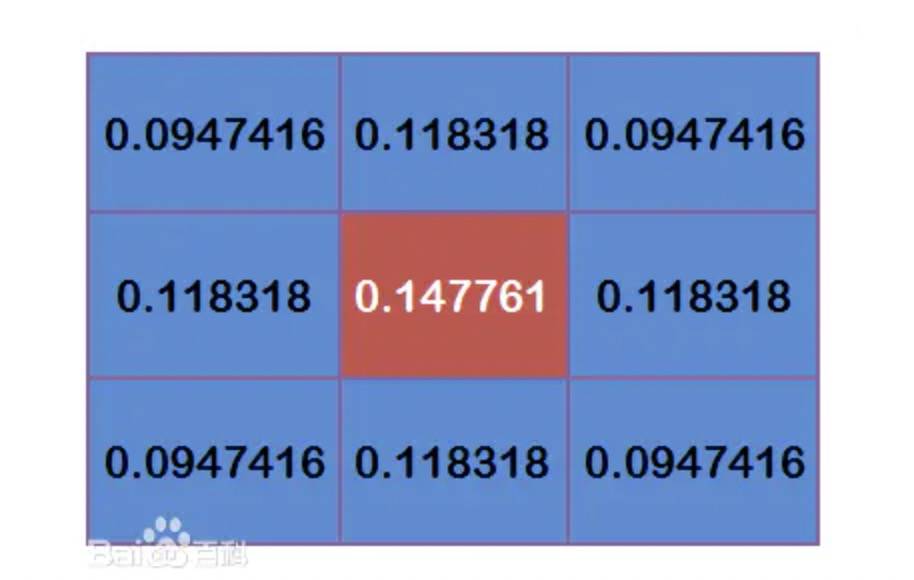
高斯模糊属于什么滤波？

这里高斯模糊和均值滤波都属于低通滤波，为什么呢？
因为它们的本质就是将目标像素取周围像素的平均值，所以边缘的差异性会降低。我们上面说过频率越高说明颜色差异越大，反过来颜色差异降低的话，频率也就降低了，相当于过滤了高频部分了。让图片更加平滑

highpass高通滤波
const weights = [
	-1, -1, -1,
	-1, 8, -1,
	-1, -1, -1,
]

这个是高通滤波的卷积核，可以看出是中间为正数，其余8个为-1，它们之和为0,经过该滤波器，可以看出如果中间的值比四周的大，则会得到放大期和周围的差值，相反比四周的小的话，则得到的是负数，即黑色。这样就会得到图片的边缘图。

laplacian拉普拉斯滤波
const weights = [
	0, -1, 0,
	-1, 4, -1,
	0, -1, 0,
]

拉普拉斯滤波也属于高通滤波，不过它比较的像素点是上下左右四个，不过最终还是能得到图片的边缘效果

应用场景

识别滑块图形验证码

操作步骤如下

制作各式各样滤镜的图片

// 浮雕滤波器
[
-1, -1, 0,
-1, 0, 1,
0, 1, 1
]

// 运动模糊
[
1/3, 0, 0,
0, 1/3, 0,
0, 0, 1/3, 
]

标签：const,卷积,滤波,let,图片,通滤波
来源： https://www.cnblogs.com/suyuanli/p/14934463.html