关键路径(Critical Path)
作者:互联网
引入
拓扑排序主要是为解决一个工程能否顺序进行的问题,但有时还需要解决工程完成需要的最短时间问题。这时仅仅是拓扑排序是不够的。
通过拓扑排序,可以有效地分析出一个有向图是否存在环;若不存在,那它的拓扑排序是什么?另一方面,利用求关键路径的算法,可以得到完成工程的最短工期及关键活动有哪些。(摘自《大话数据结构》)
定义
事件:开始XX事情 | 完成XX事情
活动:做XX事情
源点:某流程的开始
汇点:某流程的结束
AOE网:在一个表示工程的带权有向图中,用顶点表示事件,用有向边表示活动,用边上的权值表示活动的持续时间,这种有向图的边表示活动的网,我们称之为AOE网(Activity On Edge Network)。
把路径上各个活动所持续的时间之和称为路径长度,从源点到汇点具有最大长度的路径叫关键路径,在关键路径上的活动叫关键活动。(摘自《大话数据结构》)事件是一个点,活动是一条线。
举例
以炒一盘肉作为示例:将炒一盘肉比作一个工程。一位大人负责厨房的事情,一位小孩负责从院子里摘菜并送到厨房。小孩从院子里摘菜并送到厨房需要1.5分钟。大人准备肉需要7分钟;准备菜需要1.5分钟;炒肉需要2分钟;炒菜需要1分钟。
问题:这项工程的最短时间为多少?
显然,该工程的流程不是这样:摘菜送到厨房(1.5分钟)->准备肉(7分钟)->准备菜(1.5分钟)->炒肉(2分钟)->炒菜(1分钟),共13分钟。因为小孩摘菜的同时大人可以准备肉;在炒肉的后面阶段可以将菜放入锅里一起炒,这也符合日常实践。而准备菜这个活动又受到“摘菜并送到厨房”和“准备肉”这两个活动的制约:先有菜才能对菜进行处理!先处理好肉才能处理菜吧,厨房里只有一个人。
用前面的“事件”、“活动”、“源点”和“汇点”来表示这个工程。
源点:开始准备肉/开始摘菜送到厨房
汇点:完成炒菜/完成炒肉
事件:
开始摘菜并送到厨房>完成摘菜并送到厨房
开始准备肉>完成准备肉
开始准备菜>完成准备菜
开始炒肉>完成炒肉
开始炒菜>完成炒菜
约束条件:“完成准备肉”和“完成摘菜并送到厨房”才能“开始准备菜”。
活动:
摘菜送到厨房(历时1.5分钟)
准备肉(历时7分钟)
准备菜(历时1.5分钟)
炒肉(历时2分钟)
炒菜(历时1分钟)
若将此工程绘成有向图,可表示如下:
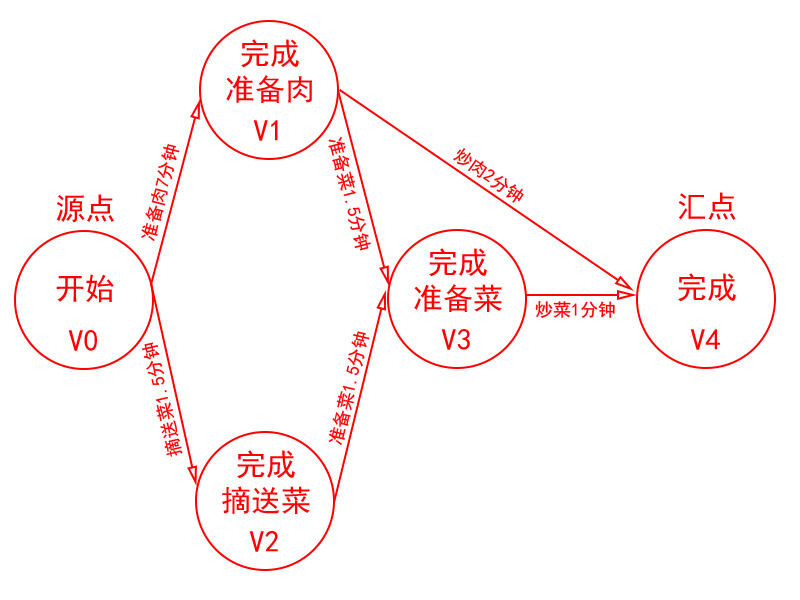
问题1(引入etv):各个事件(顶点)的最早开始时间是多少?引入词汇Earliest Time of Vertex(etv)来表示最早开始时间。Etv[0]表示顶点v0的最早开始时间。
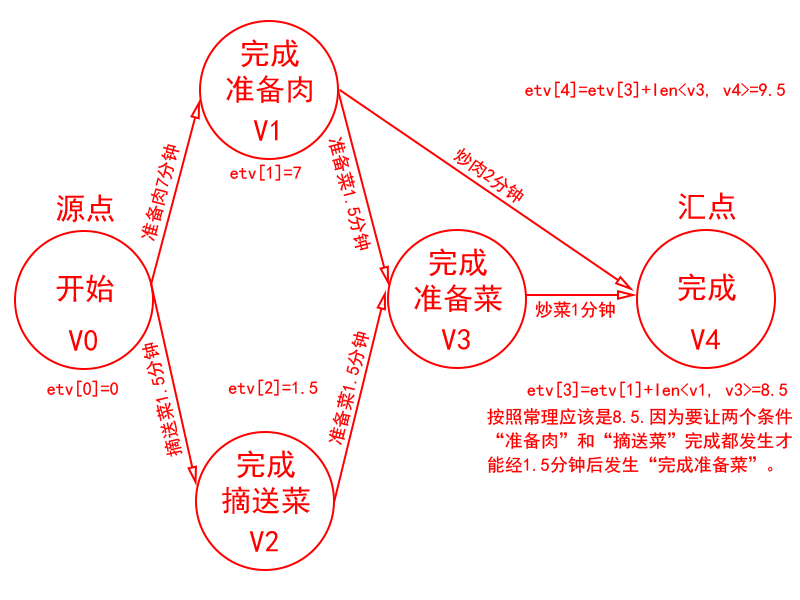
问题1总结:
etv[k]=0, 当k=0时。
etv[k]=max{etv[i]+len<vi, vk>},当k≠0且<vi, vk>∈P[k]时,其中P[k]是到达顶点vk的弧的集合。
对结果数据含义的解释:
etv[0]:开始准备肉/开始摘菜并送菜最早于第0分钟发生。
etv[1]:完成准备肉/开始准备菜/开始炒肉最早于第7分钟发生。
etv[2]:完成摘菜并送菜/开始准备菜最早于第1.5分钟发生。
etv[3]:完成准备菜/开始炒菜最早于第8.5分钟发生。
etv[4]:完成炒肉/完成炒菜最早于第9分钟发生。
问题2(引入ltv):各个事件(顶点)的最晚开始时间是多少?引入词汇Latest Time of Vertex(Ltv)表示最晚开始时间。Ltv[0]表示顶点v0的最晚开始时间。
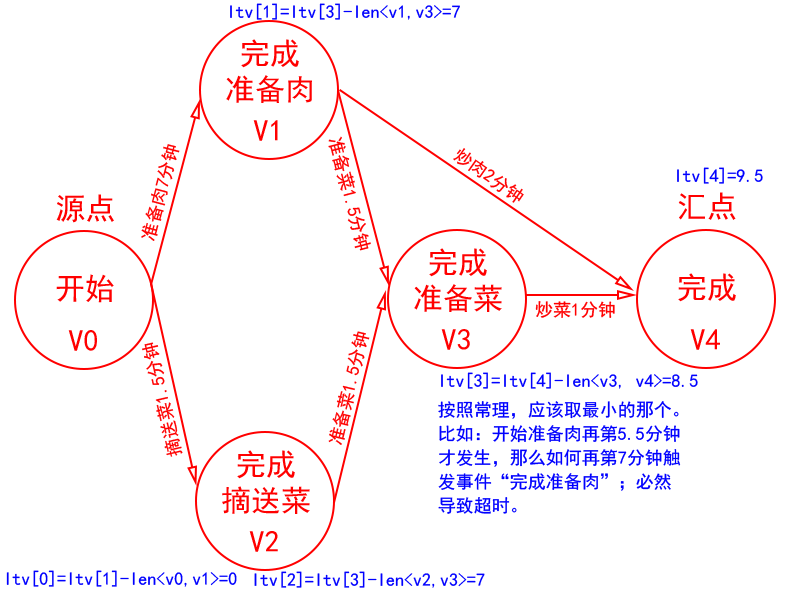
问题2总结:
ltv[k] = etv[k],当k=n-1时(n为图G的顶点数)
ltv[k] = min{etv[i]-len<vk, vi>}当k<n-1且<vk, vi>∈S[k]其中S[k]是从vk出发的弧的集合。len<vk, vi>是弧<vk, vi>的权值。
对结果数据含义的解释:
ltv[0]:开始准备肉/开始摘菜最晚于第0分钟发生。
ltv[1]:完成准备肉/开始准备菜最晚于第7分钟发生。
ltv[2]:完成摘菜并送菜/开始准备菜最晚于第7分钟发生。
ltv[3]:完成准备菜/开始炒菜最晚于第8.5分钟发生。
ltv[4]:完成炒肉/完成炒菜最晚于第9.5分钟发生。
问题3(引入问题):完成此工程的最短时间是多少?由于ltv[4]=9.5,按其含义即可知最晚于9.5分钟完成工程。
问题4(引入ete/lte):完成整个工程的过程中,有哪些活动是对整个工程的时间起决定作用的?
观察:
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| etv | 0 | 7 | 1.5 | 8.5 | 9.5 |
| ltv | 0 | 7 | 7 | 8.5 | 9.5 |
顶点v0,v1,v3,v4的etv与ltv,意味着这些顶点代表的事件的最早开始时间和最晚开始时间相等,即这些事件是刻不容缓的。所以是不是将这些顶点连接起来所形成的路径就是完成整个工程所需要经过的路径呢?看起来有点像:
v4之前的顶点有v1和v3且他们的etv和ltv都相等,所以路径为v1->v4,v3->v1吗?v3和v1的etv和ltv也相等所以,v1->v3也是所求路径?v0和v1的etv和ltv也相等,那么v0->v1也是?
回到本文开头。用弧表示活动,即弧(边)表示做某事,如“炒肉”这件活动。那么,上图中一共有6条弧(边),哪些弧所代表的活动是最刻不容缓的?什么条件满足才能显示出此活动刻不容缓?
为此引入词汇:“活动最早开始时间”(Earliest Time of Edge)和“活动最晚开始时间”(Latest Time of Edge)。
计算各弧(边)的Ete和Lte
以v0点为起点,对于弧(边)<v0, v2>,etv[0]=0,ltv[2]=7,len<v0, v2>=1.5,那么弧<v0, v2>的ete为ete=etv[0]=0,从事件v0开始的活动,自然最早也只能是etv[0]这个时刻开始。而弧<v0, v2>的lte为lte=ltv[2]-len<v0, v2>=7-1.5=5.5即<v0, v2>这个活动(摘菜并送到厨房)最晚不能超过5.5才能开始。小结:<v0, v2>弧的ete=0,lte=5.5。
以v0点为起点,对于弧(边)<v0, v1>,etv[0]=0,ltv[1]=7,len<v0, v1>=7,那么弧<v0, v1>的ete为ete=etv[0]=0,从事件v0开始的活动,自然最早也只能是etv[0]这个时刻开始。而弧<v0, v1>的lte为lte=ltv[1]-len<v0, v1>=7-7=0即<v0, v1>这个活动(准备肉)最晚不能超过0才开始。小结:<v0, v1>弧的ete=0,lte=0。所以<v0, v1>这个弧是刻不容缓的。
同样地,
以v1为起点:
<v1, v3>,ete=etv[1]=7,lte=ltv[3]-len<v1, v3>=8.5-1.5=7
<v1, v4>,ete=etv[1]=7,lte=ltv[4]-len<v1, v4>=9.5-2=7.5
小结:<v1, v3>这个活动刻不容缓。
以v2为起点:
<v2, v3>,ete=etv[2]=1.5,lte=ltv[3]-len<v2, v3>=8.5-1.5=7
解释:准备菜最早可从1.5分钟开始,最晚从7分钟开始。
以v3为起点:
<v3, v4>,ete=etv[3]=8.5,lte=ltv[4]-len<v3, v4>=9.5-1=8.5
小结:<v1, v3>这个活动刻不容缓。
总结:以下这些弧所代表的活动会影响到整个工程的完成事件。若优化他们,则可改进整个工程的完成事件。
<v0, v1>、<v1, v3>、<v3, v4>
对于顶点vi,若其出边的弧头顶点为vk则ete=etv[i],lte=ltv[k]-len<vi, vk>。若ete与lte相等,则<vi, vk>是关键路径上的弧。关键路径不止一条。如:若上图的每条边的ete与lte都相等,那么关键路径就不止一条。要优化所有这些路径才能优化整个工程(图)的最短时间。
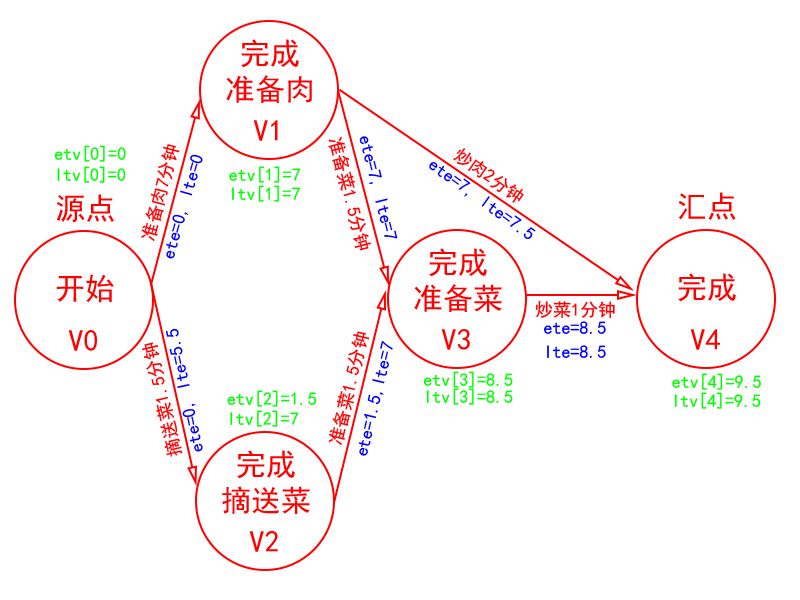
如何求得关键路径(引入拓扑排序)
完成一个工程,其中的事件是有先后顺序的,后面的事件依赖前面的事件。对于整个流程,若任意事件(vi, vj)构成路径,则vi一定在vj之前。这其实就是对事件(顶点)进行拓扑排序。
从而可知求关键路径的大致流程为:
①拓扑排序。
②求得etv数组。
③逆向地从末顶点开始求ltv数组。
④从首顶点开始遍历各顶点求ete和lte,若ete与lte相等,则该弧(边)为关键路径上的弧(边)。
给弧(边)类增加属性Weight(权值)、Ete(活动最早开始时间)、Lte(活动最晚开始时间)。
给事件(顶点)类增加属性Etv(事件最早开始事件)、Ltv(事件最晚开始时间)。
计算过程
1.用邻接表来表示有向图G。计数器counter置0。
2.将图G中的所有入度为0的顶点入栈S1。
3.新建数组Etv用于存储各顶点的Etv值,显然数组Etv长度与顶点数一样。
4.创建栈S2用于缓存S1中弹出的入度为0的顶点,待计算Ltv使用。
5.Etv数组各元素置0。
6.若栈S1不为空,则从栈中弹出一个顶点,记作vtop。
7.将vtop入栈S2.
8.计数器counter++。
9.将顶点vtop的出边弧头顶点vadj的入度减1。
10.求vtop.etv的值:如果vadj.etv < vtop.etv + len<vtop, vadj>即vtop.etv < vtop.etv + e.Weight则vtop.etv = vtop.etv + e.Weight。
11.如果vadj的入度为0,则将vadj入栈S1。
12.跳至步骤6。
13.如果计数器counter与图G的顶点数相等,则完成拓扑排序,否则意味着图G中有环,不能进行拓扑排序。
14.创建数组Ltv用于存储各顶点的Ltv值,自然数组Ltv长度与顶点数一样。
15.Ltv数组各元素的值设置为etv[n-1],其中n为图G的顶点数目。
16.若栈S2不为空,则从栈中弹出一个顶点,记作vtop。
17.遍历顶点vtop的各出边弧e(及弧e的弧头vadj)。
18.若vtop.ltv > vadj.ltv - len<vtop, vadj>则vtop.ltv= vadj.ltv - len<vtop, vadj>。
19.跳至步骤16。
20.遍历图G的顶点,计算各顶点的出边(弧)的Ete和Lte。
21.对于顶点vk其出边的Ete=etv[k];其出边的Lte=ltv[j] - len<vk, vj>=ltv[j]-e.Weight。
22.若Lte与Ete相等,则输出边或弧<vk, vj>
复杂度
拓扑排序及求Etv的时间复杂度为O(n+e),求Ltv的时间复杂度也为O(n+e),求Ete和Lte的时间复杂度也为O(n+e)。根据对时间复杂度的定义,常数系数可以忽略,所以整个求关键路径算法的时间复杂度依然是O(n+e)。其中n是顶点数目,e是弧(边)的数目。
代码
用邻接矩阵来表示图G。如前面的图。以及大话数据结构上的图,如下图:
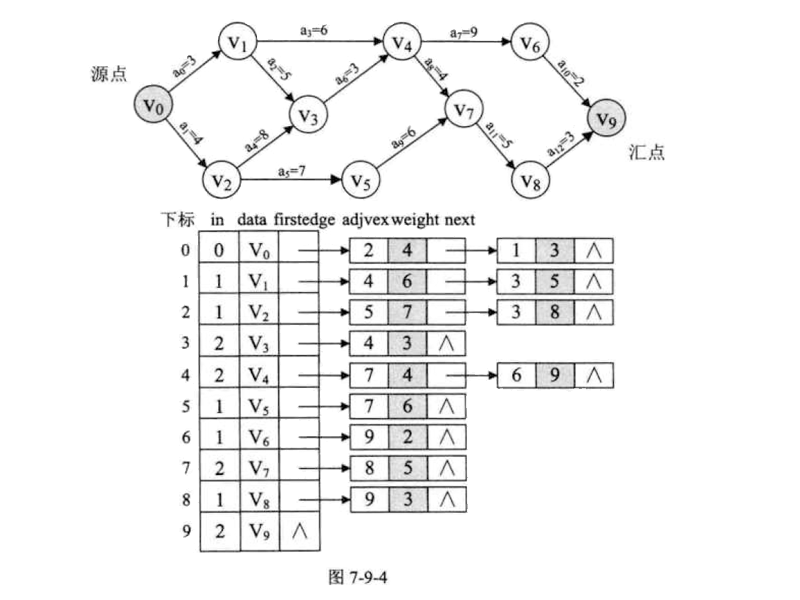
C#代码
using System;
using System.Collections.Generic;
namespace CriticalPath
{
class Program
{
static void Main(string[] args)
{
CriticalPath(new Vertex[] {
new Vertex(0,"开始",new Edge[]{new Edge(){ Vertex = 1, Weight = 70, Data="准备肉"}, new Edge(){ Vertex = 2, Weight = 15, Data = "摘送菜" } }),
//new Vertex(2,"准备蒜苗",new Edge[]{ new Edge() { Vertex = 4, Weight = 10, Data = "准备蒜苗" }, new Edge(){Vertex = 1, Weight = 10, Data = ""} }), // 让图中存在环
new Vertex(1,"完成准备肉",new Edge[]{new Edge(){ Vertex = 3, Weight = 15, Data="准备菜"}, new Edge(){ Vertex = 4, Weight = 20, Data="炒肉" } }),
new Vertex(1,"完成摘菜送菜", new Edge[]{new Edge(){ Vertex = 3, Weight = 15, Data="准备菜"}}),
new Vertex(2,"完成准备菜",new Edge[]{new Edge(){ Vertex = 4, Weight = 10, Data="炒菜"}}),
new Vertex(2,"完成",new Edge[]{}),
});
Console.WriteLine("来自《大话数据结构》P281的数据。");
// 《大话数据结构》P281的图7-9-4的数据。
CriticalPath(new Vertex[] {
new Vertex(0,"0",new Edge[]{new Edge(){ Vertex = 2, Weight = 4, Data="A1"}, new Edge(){ Vertex = 1, Weight = 3, Data = "A0" } }),
new Vertex(1,"1",new Edge[]{new Edge(){ Vertex = 4, Weight = 6, Data="A3"}, new Edge(){ Vertex = 3, Weight = 5, Data="A2"}}),
new Vertex(1,"2",new Edge[]{new Edge(){ Vertex = 5, Weight = 7, Data="A5"},new Edge(){ Vertex = 3, Weight = 8, Data="A4"}}),
new Vertex(2,"3",new Edge[]{new Edge(){ Vertex = 4, Weight = 3, Data="A6"}}),
new Vertex(2,"4",new Edge[]{new Edge(){ Vertex = 7, Weight = 4, Data="A8"},new Edge(){ Vertex = 6, Weight = 9, Data="A7"}}),
new Vertex(1,"5",new Edge[]{new Edge(){ Vertex = 7, Weight = 6, Data="A9"}}),
new Vertex(1,"6",new Edge[]{new Edge(){ Vertex = 9, Weight = 2, Data="A10"}}),
new Vertex(2,"7",new Edge[]{new Edge(){ Vertex = 8, Weight = 5, Data="A11"}}),
new Vertex(1,"8",new Edge[]{new Edge(){ Vertex = 9, Weight = 3, Data="A12"}}),
new Vertex(2,"9",new Edge[]{}),
});
}
public static void CriticalPath(Vertex[] graph)
{
List<string> results = new List<string>();
// 拓扑排序的同时计算Etv。
// 1.用于判断最终图中是否还有入度为0的顶点。若没有则拓扑排序成功。否则没有。
int counter = 0;
// 缓存入度为0的顶点。
Stack<Vertex> s1 = new Stack<Vertex>();
// 2.将所有入度为0的顶点入栈S1。
for (int i = 0; i < graph.Length; i++)
{
Vertex v = graph[i];
if (v.InDegree == 0)
{
s1.Push(v);
}
}
// 3.新建数组etv用于存储各顶点的etv值。显然,数组长度与顶点数一样。
//int[] etv = new int[graph.Length];
// 4.etv数组各元素置0。
for (int i = 0; i < graph.Length; i++)
{
graph[i].Etv = 0;
}
// 5.创建栈S2用于缓存S1中弹出的入度为0的顶点,之后用于求各顶点的ltv。
Stack<Vertex> s2 = new Stack<Vertex>();
// 6.若栈S1不为空,
while (s1.Count != 0)
{
// 则从栈中弹出一个顶点Vtop。
Vertex top = s1.Pop();
// 7.将Vtop入栈S2.
s2.Push(top);
// 8.计数器递增。
counter++;
// 9.将顶点Vtop的出边弧头Vadj的入度减1。
for (var e = top.Edge; e != null; e = e.Next)
{
// 弧头顶点在顶点数组中的索引。
int n = e.Vertex;
Vertex adj = graph[n];
// 顶点Vadj的入度减1。
adj.InDegree--;
// 10.求顶点Vadj对应的etv的值。
if (adj.Etv < top.Etv + e.Weight)
{
adj.Etv = top.Etv + e.Weight;
}
// 11.如果Vadj的入度为0,
if (adj.InDegree == 0)
{
// 则将Vadj入栈S1。
s1.Push(adj);
}
}
// 12.跳至步骤6。
}
// 13.如果计数器counter与图G的顶点数相等,则完成拓扑排序,否则意味着图G中有环,不能进行拓扑排序。
if (counter != graph.Length)
{
throw new Exception($"错误:图G中顶点数:{graph.Length},还剩{graph.Length - counter}个顶点入度非0。");
}
//else // 此程序不是为了求拓扑排序,所以不输出拓扑排序的结果。
//{
// Console.WriteLine(string.Join(",", result.ToArray()));
//}
// 准备计算Ltv。
// 14.创建数组ltv用于存储各顶点的ltv,显然数组ltv长度与顶点数一样。
//int[] ltv = new int[graph.Length];
// 15.ltv数组各元素设置为etv[n-1],其中n为图G的顶点数目。
for (int i = graph.Length - 1, n = graph.Length; i > 0; i--)
{
graph[i].Ltv = graph[n - 1].Etv;
}
// 16.若S2不为空,则从栈中弹出一个顶点Vtop。
while (s2.Count != 0)
{
Vertex top = s2.Pop();
// 17.遍历顶点Vtop的各出边弧e(及弧e的弧头Vadj)
for (var e = top.Edge; e != null; e = e.Next)
{
int n = e.Vertex;
Vertex adj = graph[n];
// 18.若top.Ltv > adj.Ltv - Len(Vtop, Vadj),则top.Ltv为adj.Ltv - Len(Vtop, Vadj)。
if (top.Ltv > adj.Ltv - e.Weight)
{
top.Ltv = adj.Ltv - e.Weight;
}
}
// 19.跳至步骤16。
}
// 20.遍历图G的顶点,计算各顶点的出边(弧)的ete和lte。
for (int i = 0; i < graph.Length; i++)
{
Vertex vk = graph[i];
// 21.对于顶点Vk,其出边的ete=etv[k];lte=ltv[j] - len<Vk, Vj> = ltv[j] - e.weight。
for (var e = vk.Edge; e != null; e = e.Next)
{
Vertex vj = graph[e.Vertex];
e.Ete = vk.Etv;
e.Lte = vj.Ltv - e.Weight;
// 22.若lte与ete相等,则输出边或弧<Vk, Vj>。
if (e.Ete == e.Lte)
{
results.Add($"关键路径:\t{e.Data}\t的最早开始时间:{e.Ete},\t最晚开始时间:{e.Lte},\t耗时:{e.Weight}");
}
else
{
results.Add($"非关键路径:\t{e.Data}\t的最早开始时间:{e.Ete},\t最晚开始时间:{e.Lte},\t耗时:{e.Weight}");
}
}
}
results.Sort();
Console.WriteLine(string.Join('\n', results.ToArray()));
}
}
/// <summary>
/// 图G的顶点。用邻接表来表示顶点的出边。
/// </summary>
public class Vertex
{
/// <summary>
/// 入度。
/// </summary>
public int InDegree { get; set; } = 0;
/// <summary>
/// 存储的数据。
/// </summary>
public string Data { get; set; } = "";
/// <summary>
/// 出边。
/// </summary>
public Edge Edge { get; set; } = null;
/// <summary>
/// 事件的最早开始时间。
/// </summary>
public int Etv { get; set; } = 0;
/// <summary>
/// 事件的最晚开始时间。
/// </summary>
public int Ltv { get; set; } = 0;
public Vertex(int inDegree, string data, Edge[] adjacentEdges)
{
this.InDegree = inDegree;
this.Data = data;
Edge e = null;
for (int i = 0; i < adjacentEdges.Length; i++)
{
if (e == null)
{
e = new Edge(adjacentEdges[i].Vertex, adjacentEdges[i].Weight, adjacentEdges[i].Data, null);
this.Edge = e;
}
else
{
e.Next = new Edge(adjacentEdges[i].Vertex, adjacentEdges[i].Weight, adjacentEdges[i].Data, null);
e = e.Next;
}
}
}
}
/// <summary>
/// 图G的边。以邻接表表示顶点的出边。
/// </summary>
public class Edge
{
/// <summary>
/// 边的弧头顶点在顶点数组中的索引。
/// </summary>
public int Vertex { get; set; } = -1;
/// <summary>
/// 边的弧尾顶点的下一条出边。
/// </summary>
public Edge Next { get; set; } = null;
/// <summary>
/// 边的权重。
/// </summary>
public int Weight { get; set; } = 0;
/// <summary>
/// 事件的描述。
/// </summary>
public string Data { get; set; } = string.Empty;
/// <summary>
/// Earliest Time of Edge.(事件的最早发生时间。)
/// </summary>
public int Ete { get; set; }
/// <summary>
/// Latest Time of Edge.(事件的最晚发生时间。)
/// </summary>
public int Lte { get; set; }
public Edge(int vertex = -1, int weight = 0, string data = "", Edge edge = null)
{
this.Vertex = vertex;
this.Next = edge;
this.Weight = weight;
this.Data = data;
}
}
}
/**
运行结果:
非关键路径: 炒肉 的最早开始时间:70, 最晚开始时间:75, 耗时:20
非关键路径: 摘送菜 的最早开始时间:0, 最晚开始时间:55, 耗时:15
非关键路径: 准备菜 的最早开始时间:15, 最晚开始时间:70, 耗时:15
关键路径: 炒菜 的最早开始时间:85, 最晚开始时间:85, 耗时:10
关键路径: 准备菜 的最早开始时间:70, 最晚开始时间:70, 耗时:15
关键路径: 准备肉 的最早开始时间:0, 最晚开始时间:0, 耗时:70
来自《大话数据结构》P281的数据。
非关键路径: A0 的最早开始时间:0, 最晚开始时间:4, 耗时:3
非关键路径: A10 的最早开始时间:24, 最晚开始时间:25, 耗时:2
非关键路径: A2 的最早开始时间:3, 最晚开始时间:7, 耗时:5
非关键路径: A3 的最早开始时间:3, 最晚开始时间:9, 耗时:6
非关键路径: A5 的最早开始时间:4, 最晚开始时间:6, 耗时:7
非关键路径: A7 的最早开始时间:15, 最晚开始时间:16, 耗时:9
非关键路径: A9 的最早开始时间:11, 最晚开始时间:13, 耗时:6
关键路径: A1 的最早开始时间:0, 最晚开始时间:0, 耗时:4
关键路径: A11 的最早开始时间:19, 最晚开始时间:19, 耗时:5
关键路径: A12 的最早开始时间:24, 最晚开始时间:24, 耗时:3
关键路径: A4 的最早开始时间:4, 最晚开始时间:4, 耗时:8
关键路径: A6 的最早开始时间:12, 最晚开始时间:12, 耗时:3
关键路径: A8 的最早开始时间:15, 最晚开始时间:15, 耗时:4
*/
TypeScript代码
/**
* 图G的顶点。用邻接表来表示顶点的出边。
*/
class Vertex {
// 入度。
InDegree: number = 0;
// 存储的数据。
Data: string = "";
// 首条出边。
Edge: Edge = null;
// 事件的最早开始时间。
Etv: number = 0;
// 事件的最晚开始时间。
Ltv: number = 0;
/**
* 创建邻接表的一行。
* @param inDegree 顶点的入度。
* @param data 顶点存储的数据。
* @param adjacentEdges 从该顶点出发的弧。
*/
constructor(inDegree: number, data: string, adjacentEdges: Edge[]) {
this.InDegree = inDegree;
this.Data = data;
let e: Edge = null;
for (let i = 0; i < adjacentEdges.length; i++) {
if (e === null) {
e = new Edge(adjacentEdges[i].Vertex, adjacentEdges[i].Weight, adjacentEdges[i].Data, null);
this.Edge = e;
}
else {
e.Next = new Edge(adjacentEdges[i].Vertex, adjacentEdges[i].Weight, adjacentEdges[i].Data, null);
e = e.Next;
}
}
}
}
/**
* 图G的边。以邻接表表示顶点的出边。
*/
class Edge {
// 边的弧头顶点在顶点数组中的索引。
Vertex: number = -1;
// 边的弧尾顶点的下一条出边。
Next: Edge = null;
// 边的权重。
Weight: number = 0;
// 事件的描述。
Data: string = "";
// Earlist Time of Edge.(事件的最早发生时间。)
Ete: number = 0;
// Latest Time of Edge.(事件的最晚发生时间。)
Lte: number = 0;
/**
* 创建邻接表中的一条边/弧。
* @param vertex 邻接表中,该边的弧尾顶点的在顶点数组中的下标。
* @param weight 弧的权重。
* @param data 事件的描述。
* @param next 邻接表中,该边的弧尾顶点的下一条出边。
*/
constructor(vertex: number = -1, weight: number = 0, data: string = "", next: Edge = null) {
this.Vertex = vertex;
this.Next = next;
this.Weight = weight;
this.Data = data;
}
}
function criticalPath(graph: Vertex[]) {
let results: string[] = [];
// 拓扑排序的同时计算Etv。
// 1.用于判断最终图中是否还有入度为0的顶点。若没有则拓扑排序成功。否则没有。
let counter: number = 0;
// 缓存入度为0的顶点。
let s1: Vertex[] = [];
// 2.将所有入度为0的顶点入栈S1。
for (let i = 0; i < graph.length; i++) {
let v: Vertex = graph[i];
if (v.InDegree === 0) {
s1.push(v);
}
}
// 3.新建数组etv用于存储各顶点的etv值。显然,数组长度与顶点数一样。
// let etv:number[] = [];
// 4.etv数组各元素置0。
for (let i = 0; i < graph.length; i++) {
graph[i].Etv = 0;
}
// 5.创建栈S2用于缓存S1中弹出的入度为0的顶点,之后用于求各顶点的Ltv。
let s2: Vertex[] = [];
// 6.若栈S1不为空,
while (s1.length != 0) {
// 则从栈中弹出一个顶点Vtop。
let top: Vertex = s1.pop();
// 7.将Vtop入栈S2。
s2.push(top);
// 8.计数器递增。
counter++;
// 9.将顶点Vtop的出边弧头Vadj的入度减1。
for (let e = top.Edge; e != null; e = e.Next) {
// 弧头顶点在顶点数组中的索引。
let n: number = e.Vertex;
let adj: Vertex = graph[n];
// 顶点Vadj的入度减1。
adj.InDegree--;
// 10.求顶点Vadj对应的etv的值。
if (adj.Etv < top.Etv + e.Weight) {
adj.Etv = top.Etv + e.Weight;
}
// 11.如果Vadj的入度为0,
if (adj.InDegree == 0) {
// 则将Vadj入栈S1。
s1.push(adj);
}
}
// 12.跳至步骤6。
}
// 13.如果计数器counter与图G的顶点数相等,则完成拓扑排序,否则意味着图G中有环,不能进行拓扑排序。
if (counter != graph.length) {
throw new Error(`错误:图G中顶点数:${graph.length},还剩${graph.length - counter}个顶点入度非0。`);
}
// 14.创建数组ltv用于存储各顶点的ltv,显然数组ltv长度与顶点数一样。
// let ltv:number[] = [];
// 15.ltv数组各元素设置为etv[n-1],其中n为图G的顶点数目。
for (let i: number = graph.length - 1, n: number = graph.length; i > 0; i--) {
graph[i].Ltv = graph[n - 1].Etv;
}
// 16.若S2不为空,则从栈中弹出一个顶点Vtop。
while (s2.length != 0) {
let top: Vertex = s2.pop();
// 17.遍历顶点Vtop的各出边弧e(及弧e的弧头Vadj)
for (let e = top.Edge; e != null; e = e.Next) {
let n: number = e.Vertex;
let adj: Vertex = graph[n];
// 18.若top.Ltv > adj.Ltv - Len(Vtop, Vadj),则top.Ltv为adj.Ltv - Len(Vtop, Vadj)。
if (top.Ltv > adj.Ltv - e.Weight) {
top.Ltv = adj.Ltv - e.Weight;
}
}
// 19.跳至步骤16。
}
// 20.遍历图G的顶点,计算各顶点的出边(弧)的ete和lte。
for (let i: number = 0; i < graph.length; i++) {
let vk: Vertex = graph[i];
// 21.对于顶点Vk,其出边的ete=etv[k];lte=ltv[j] - len<Vk, Vj> = ltv[j] - e.weight。
for (let e: Edge = vk.Edge; e != null; e = e.Next) {
let vj: Vertex = graph[e.Vertex];
e.Ete = vk.Etv;
e.Lte = vj.Ltv - e.Weight;
// 22.若lte与ete相等,则输出边或弧<Vk, Vj>。
if (e.Ete == e.Lte) {
results.push(`关键路径:\t${e.Data}\t的最早开始时间:${e.Ete},\t最晚开始时间:${e.Lte},\t耗时:${e.Weight}`);
}
else {
results.push(`非关键路径:\t${e.Data}\t的最早开始时间:${e.Ete},\t最晚开始时间:${e.Lte},\t耗时:${e.Weight}`);
}
}
}
results.sort();
console.log(results.join('\n'));//string.Join('\n', results.ToArray()));
}
function main() {
criticalPath([
new Vertex(0, "开始", [new Edge(1, 70, "准备肉"), new Edge(2, 15, "摘送菜")]),
//new Vertex(2,"准备蒜苗",[new Edge(4, 10, "准备蒜苗"), new Edge(1, 10, "") ]), // 让图中存在环
new Vertex(1, "完成准备肉", [new Edge(3, 15, "准备菜"), new Edge(4, 20, "炒肉")]),
new Vertex(1, "完成摘菜送菜", [new Edge(3, 15, "准备菜")]),
new Vertex(2, "完成准备菜", [new Edge(4, 10, "炒菜")]),
new Vertex(2, "完成", [])
]);
console.log("来自《大话数据结构》P281的数据。");
criticalPath([
new Vertex(0, "0", [new Edge(2, 4, "A1"), new Edge(1, 3, "A0")]),
new Vertex(1, "1", [new Edge(4, 6, "A3"), new Edge(3, 5, "A2")]),
new Vertex(1, "2", [new Edge(5, 7, "A5"), new Edge(3, 8, "A4")]),
new Vertex(2, "3", [new Edge(4, 3, "A6")]),
new Vertex(2, "4", [new Edge(7, 4, "A8"), new Edge(6, 9, "A7")]),
new Vertex(1, "5", [new Edge(7, 6, "A9")]),
new Vertex(1, "6", [new Edge(9, 2, "A10")]),
new Vertex(2, "7", [new Edge(8, 5, "A11")]),
new Vertex(1, "8", [new Edge(9, 3, "A12")]),
new Vertex(2, "9", []),
]);
}
main();
/**
运行结果:
关键路径: 准备肉 的最早开始时间:0, 最晚开始时间:0, 耗时:70
关键路径: 准备菜 的最早开始时间:70, 最晚开始时间:70, 耗时:15
关键路径: 炒菜 的最早开始时间:85, 最晚开始时间:85, 耗时:10
非关键路径: 准备菜 的最早开始时间:15, 最晚开始时间:70, 耗时:15
非关键路径: 摘送菜 的最早开始时间:0, 最晚开始时间:55, 耗时:15
非关键路径: 炒肉 的最早开始时间:70, 最晚开始时间:75, 耗时:20
来自《大话数据结构》P281的数据。
关键路径: A1 的最早开始时间:0, 最晚开始时间:0, 耗时:4
关键路径: A11 的最早开始时间:19, 最晚开始时间:19, 耗时:5
关键路径: A12 的最早开始时间:24, 最晚开始时间:24, 耗时:3
关键路径: A4 的最早开始时间:4, 最晚开始时间:4, 耗时:8
关键路径: A6 的最早开始时间:12, 最晚开始时间:12, 耗时:3
关键路径: A8 的最早开始时间:15, 最晚开始时间:15, 耗时:4
非关键路径: A0 的最早开始时间:0, 最晚开始时间:4, 耗时:3
非关键路径: A10 的最早开始时间:24, 最晚开始时间:25, 耗时:2
非关键路径: A2 的最早开始时间:3, 最晚开始时间:7, 耗时:5
非关键路径: A3 的最早开始时间:3, 最晚开始时间:9, 耗时:6
非关键路径: A5 的最早开始时间:4, 最晚开始时间:6, 耗时:7
非关键路径: A7 的最早开始时间:15, 最晚开始时间:16, 耗时:9
非关键路径: A9 的最早开始时间:11, 最晚开始时间:13, 耗时:6
*/
参考资料
《大话数据结构》 - 程杰 著 - 清华大学出版社
标签:etv,Weight,路径,Vertex,Edge,new,Critical,Path,顶点 来源: https://www.cnblogs.com/kokiafan/p/14878327.html