单调队列的浅显讲解

概念

• 1.单调队列是一种队列 废话 ，但它不同于普通的队列，它支持两头操作，也就是既可以在队尾，也可以在队首进行操作，比如弹出，可以弹头也可以弹尾

• 2.单调队列中的元素（单调队列中，一般是对应元素的下标存储在其之中，这里指存储的下标对应的元素）满足单调性，也就是单调队列中的数是满足单调递增/递减/或是其他的性质

下面我们结合LuoguP1886 滑动窗口来具体理解单调队列

题目

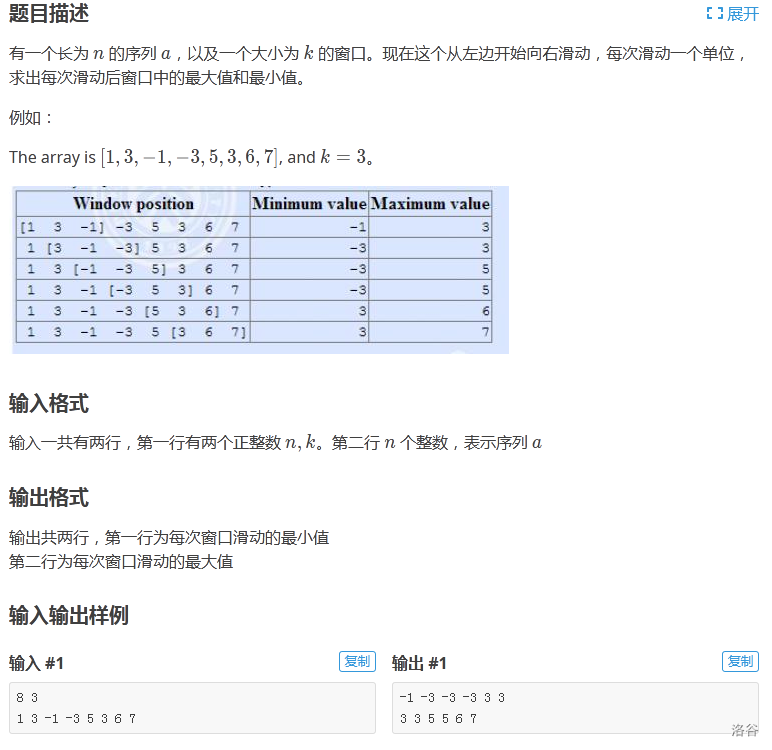
题目说的非常明确，这里不再赘述

我们来看题目中给的表格，发现这个“窗口”实际上非常像一个双向的队列，每次向右移动一个数的位置，尾去掉，新加入一个头，满足队列先进先出的性质，题目还要求我们求最大和最小值，而单调队列的特殊性就可以让我们很方便的得出答案，因此这题我们采用单调队列来解决

当然如果你非得用线段树也无所谓

思路

先来把定义挂这里

#include<cstdio>
#include<iostream>
#include<queue>
using namespace std;
struct node
{
    int sum,num;//sum是这个数的数值，num是这个数在输入数组中的下标
}a[1000005];
deque<node> s;//deque是C++自带库里的双向队列（即可以双向操作），非常方便
int n,k;//与题目中一致

我们先来考虑个简单的问题，既然这是一个“窗口”，那么肯定窗口划过去之后，我们相应的队列中的值也得去掉，这叫做“去尾”

while (s.back().num<=i-k) s.pop_back(); // i 为当前的队头的下标， k 为窗口大小

然后我们来考虑如何让一个元素加入队列，并且不影响到队列的单调性？

实际上非常简单，和单调栈的实现方法差不多，我们只需要把加入的元素和现在的队头作比较，看是否满足最大or最小，就可以了,这个叫做“删头”

while(!s.empty()&&a[i].sum  满足条件（≥ or ≤）  s.front().sum） {s.pop_front();}//队头小于等于或者大于等于现在窗口到达的数就弹出队头，找到能让现在窗口到达元素放入的位置
s.push_front(a[i]);//入队
        

然后我们来看一下完整的过程

while (!s.empty() && a[i].sum 更符合所求的要求 s.front().sum) s.pop_front();
s.push_front(a[i]); // 现在的队头打得过更新到的数了
while (s.back().num <= i - k) s.pop_back();
printf("%d", s.back().sum); // 队尾的是当前最符合要求的数，为什么呢？看下面

刚才的两个操作分析完了，我们来分析一下那个是最符合性质的数。

每一个数都比后一个数更符合性质

所以就是第一个数了(也就是队尾）。

AC Code

#include<cstdio>
#include<iostream>
#include<queue>
using namespace std;
struct node
{
    int sum,num;
}a[1000005];
deque<node> s;
int n,k;
inline void small()
{
    for(int i=1; i<=n;i++)
    {
        while(!s.empty()&&a[i].sum<=s.front().sum) s.pop_front();
        s.push_front(a[i]);
        while(s.back().num<=i-k) s.pop_back();
        if(i>=k) printf("%d ",s.back().sum);
    }
}
inline void big()
{
    for(int i=1; i<=n;i++)
    {
        while(!s.empty()&&a[i].sum>=s.front().sum) s.pop_front();
        s.push_front(a[i]);
        while(s.back().num<=i-k) s.pop_back();
        if(i>=k) printf("%d ",s.back().sum);
    }
}
//实际上你会发现这俩操作的差别微乎其微
int main()
{
    cin>>n>>k;
    for(int i=1; i<=n;i++)
    {
        scanf("%d",&a[i].sum);
        a[i].num=i;
    }
    small();
    s.clear();
    cout<<endl;
    big();
    return 0;
}

标签：队列,sum,int,浅显,front,include,单调
来源： https://www.cnblogs.com/Edolon/p/14850994.html