洛谷P4515 [COCI2009-2010#6] XOR

洛谷P4515

这里给出的是一种复杂度为 \(\mathcal O(nS)\) 的做法，其中 \(S\) 为值域。

Description

坐标系下有若干个等腰直角三角形，且每个等腰直角三角形的直角顶点都在左下方，两腰与坐标轴平行。被奇数个三角形覆盖的面积部分为灰色，被偶数个三角形覆盖的面积部分为白色，如下图所示。

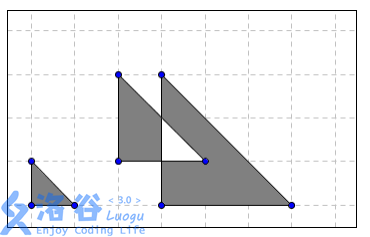
已知 \(n\) 个等腰直角三角形的顶点坐标及腰长，求灰色部分面积。

\(n\le 10\)，等腰直角三角形的横纵坐标及腰长 \(\le 10^6\).

Solution

考虑分别考虑坐标系中每一行哪些格子为灰色部分，然后将所有行的答案加起来。容易发现每个格子要么被完全覆盖，要么左下部分被覆盖，因此可以将每个格子拆成左下与右上两部分作为新的格子，那么三角形就只能覆盖整数个格子了。

考虑从第 \(x\) 行移动到 \(x-1\) 行的过程中每个三角形覆盖格子的变化：

• 这两行都不在三角形的覆盖范围中：没有变化。
• 都在覆盖范围中，则只会在最右侧多覆盖两个格子，例如下图中的情况。

• 若第 \(x\) 行在覆盖范围内而第 \(x-1\) 行不在，那么需要将原本被覆盖的位置的覆盖状态均会被修改。
• 第 \(x\) 行不在覆盖范围内，而第 \(x-1\) 行在，那么只会多覆盖一个格子。

第三种情况每个三角形最多出现一次，设 \(S\) 为值域，那么这部分最多修改 \(\mathcal O(nS)\) 个格子。第二、四种情况中，每次移动只会影响 \(1\) 个 或 \(2\) 个格子的变化情况，因此总共也只会造成 \(\mathcal O(nS)\) 次修改。于是，我们可以直接暴力用 \(bool\) 数组维护每个格子的状态，总修改次数只有 \(\mathcal O(nS)\) 个，完全足以通过此题，甚至可以将 \(n\) 加强到 \(100\)。

Code

#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
#define mp make_pair
const int N=110;
const int MX=4e6+10;
typedef long long ll;
int n,top,tot;
ll cnt,ans;
bool b[MX];
struct triangle{
	int x,y,l,up;
}a[N];
inline void change(int x){b[x]?cnt--:cnt++;b[x]^=1;}
int main(){
	scanf("%d",&n);
	int mx=1;
	for(int i=1;i<=n;++i){
		scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].l),mx=max(mx,a[i].y+a[i].l);
		a[i].up=a[i].y+a[i].l;
	}
	for(int i=mx-1;i>=1;--i){
		for(int j=1;j<=n;++j){
			if(i>=a[j].y&&i<a[j].up){
				int tmp=a[j].up-i+a[j].x;
				change(tmp<<1);
				if(i!=a[j].up-1) change((tmp<<1)-1);
			}
			if(i==a[j].y-1){
				int tmp=a[j].up-(i+1)+a[j].x;
				for(int k=(a[j].x+1)<<1;k<=(tmp<<1);++k) change(k);
			}
		}
		ans+=cnt;
	}
	printf("%.1lf\n",ans*1.0/2.0);
	return 0;
}

标签：洛谷,COCI2009,格子,int,等腰,mathcal,XOR,三角形,覆盖
来源： https://www.cnblogs.com/tqxboomzero/p/14843016.html