「题解」agc031_e Snuke the Phantom Thief
作者:互联网
本文将同步发布于:
题目
题目链接:洛谷 AT4695、AtCoder agc031_e。
题意简述
在二维平面上,有 \(n\) 颗珠宝,第 \(i\) 颗珠宝在 \((x_i,y_i)\) 的位置,价值为 \(v_i\)。
现在有一个盗贼想要偷这些珠宝。
现在给出 \(m\) 个限制约束偷的珠宝,约束有以下四种:
- 横坐标小于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗。
- 横坐标大于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗。
- 纵坐标小于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗。
- 纵坐标大于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗。
现在问你在满足这些约束的条件下,盗贼偷的珠宝的最大价值和是多少。
题解
约束与转化
这个约束有点难办,似乎并没有可能对其进行动态规划,因此我们考虑额外添加信息。
我们添加什么信息呢?考虑到限制是有关珠宝数量的,我们决定添加一个 偷珠宝的总数 的信息。
设偷珠宝 \(k\) 颗,并且珠宝按照的横坐标排序被偷的顺序编号为 \(1\sim k\),那么前两种限制条件转化如下:
- 横坐标小于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗:
若一个珠宝的编号 \(\texttt{id}\in[b_i+1,k]\),那么一定有 \(x_{\texttt{id}}>a_i\)。 - 横坐标大于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗:
若一个珠宝的编号 \(\texttt{id}\in[1,k-b_i]\),那么一定有 \(x_{\texttt{id}}<a_i\)。
同理,我们可以得出珠宝按照的纵坐标排序被偷的顺序编号为 \(1\sim k\),那么后两种限制条件转化如下:
- 纵坐标小于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗:
若一个珠宝的编号 \(\texttt{id}\in[b_i+1,k]\),那么一定有 \(y_{\texttt{id}}>a_i\)。 - 纵坐标大于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗:
若一个珠宝的编号 \(\texttt{id}\in[1,k-b_i]\),那么一定有 \(y_{\texttt{id}}<a_i\)。
因此,我们得出,一个珠宝想要在按横坐标排序为第 \(i\),纵坐标排序为第 \(j\) 时被偷,需要满足的坐标范围。
化腐朽为神奇的网络流
考虑上面的条件也不是很好动态规划,我们需要想到一种化腐朽为神奇的算法——网络流。
由于这个题目有多个互不相关的限制:
- 珠宝不能同时被偷两次及以上;
- 偷的珠宝价值要最大化;
我们考虑运用费用流建立网络流模型。
因为我们要限制横坐标,所以必须要有 \(k\) 个横坐标的限制,对应 \(s\to p_{1\sim k}\),流量为 \(1\),费用为 \(0\)。。
因为我们要限制纵坐标,所以必须要有 \(k\) 个纵坐标的限制,对应 \(q_{1\sim k}\to t\),流量为 \(1\),费用为 \(0\)。
因为我们要限制一个点不能被选择多次,所以我们需要拆点限流,对应 \(a_{1\sim n}\to b_{1\sim n}\),流量为 \(1\),费用为 \(v_i\)。
考虑到我们上面需要满足的限制,按照限制加边 \(p_i\to a_j\) 和 \(b_j\to q_i\) 即可,流量为 \(1\),费用为 \(0\)。
如果上面的语言有点抽象,我们不妨画图理解。
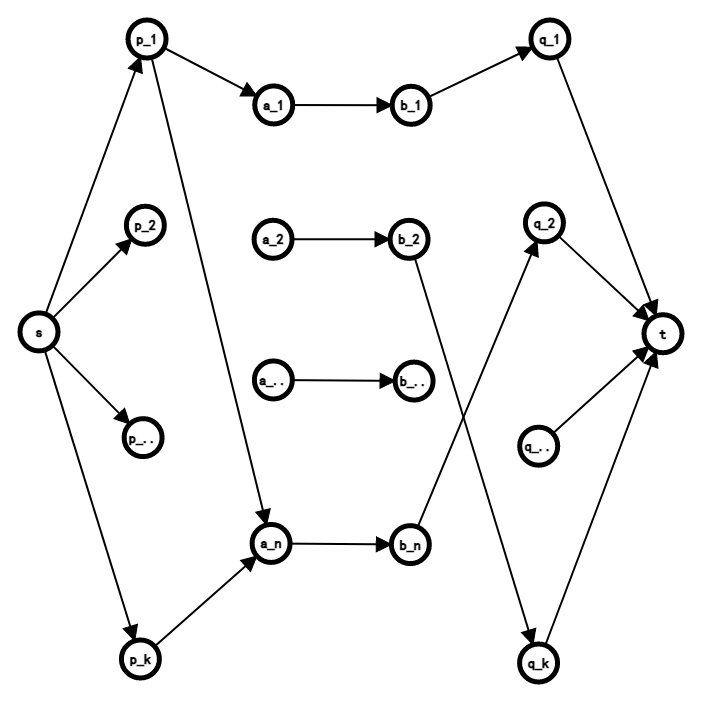
整个建图如上所示,点数为 \(\Theta(n^2)\),边数 \(\Theta(n^2)\)。
参考程序
#include<bits/stdc++.h>
using namespace std;
#define reg register
typedef long long ll;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
static char buf[1<<21],*p1=buf,*p2=buf;
inline int read(void){
reg char ch=getchar();
reg int res=0;
while(!isdigit(ch))ch=getchar();
while(isdigit(ch))res=10*res+(ch^'0'),ch=getchar();
return res;
}
inline ll readll(void){
reg char ch=getchar();
reg ll res=0;
while(!isdigit(ch))ch=getchar();
while(isdigit(ch))res=10*res+(ch^'0'),ch=getchar();
return res;
}
inline int max(reg int a,reg int b){
return a>b?a:b;
}
inline int min(reg int a,reg int b){
return a<b?a:b;
}
inline ll max(reg ll a,reg ll b){
return a>b?a:b;
}
const int MAXN=80+5;
const int MAXM=320+5;
const int inf=0x3f3f3f3f;
namespace Network{
const int MAXV=4*MAXN;
const int MAXE=(MAXN*MAXN*2+3*MAXN)*2;
const ll inf=0x3f3f3f3f3f3f3f3f;
int cnt,head[MAXV],to[MAXE],w[MAXE],Next[MAXE];
ll p[MAXE];
inline void Add_Edge(reg int u,reg int v,reg int len,reg ll val){
Next[++cnt]=head[u];
to[cnt]=v,w[cnt]=len,p[cnt]=val;
head[u]=cnt;
return;
}
inline void Add_Tube(reg int u,reg int v,reg int len,reg ll val){
Add_Edge(u,v,len,val);
Add_Edge(v,u,0,-val);
return;
}
bool inque[MAXV];
int cur[MAXV];
ll dis[MAXV];
queue<int> Q;
inline bool spfa(int s,reg int t){
fill(dis+s,dis+t+1,inf);
inque[s]=true,dis[s]=0,Q.push(s);
while(!Q.empty()){
reg int u=Q.front();
Q.pop();
inque[u]=false;
cur[u]=head[u];
for(reg int i=head[u];i;i=Next[i]){
int v=to[i];
if(dis[v]>dis[u]+p[i]&&w[i]){
dis[v]=dis[u]+p[i];
if(!inque[v]){
inque[v]=true;
Q.push(v);
}
}
}
}
return dis[t]!=inf;
}
bool vis[MAXV];
inline int dfs(reg int u,reg int t,reg ll lim){
if(u==t)
return lim;
vis[u]=true;
reg int flow=0;
for(reg int &i=cur[u];i;i=Next[i]){
reg int v=to[i];
if(dis[v]==dis[u]+p[i]&&w[i]&&!vis[v]){
reg int f=dfs(v,t,min(lim-flow,w[i]));
if(f){
flow+=f;
w[i]-=f,w[i^1]+=f;
if(flow==lim)
break;
}
}
}
vis[u]=false;
return flow;
}
inline pair<int,ll> dinic(reg int s,reg int t){
int res=0;
ll cost=0;
while(spfa(s,t)){
reg int flow=dfs(s,t,inf);
res+=flow,cost+=flow*dis[t];
}
return make_pair(res,cost);
}
inline void init(reg int s,reg int t){
cnt=1,fill(head+s,head+t+1,0);
return;
}
}
struct Point{
int x,y;
ll v;
};
struct Limits{
char ch;
int a,b;
};
struct Interval{
int l,r;
inline Interval(reg int l=0,reg int r=0):l(l),r(r){
return;
}
inline bool in(reg int x)const{
return l<=x&&x<=r;
}
};
inline Interval cap(const Interval& a,const Interval& b){
return Interval(max(a.l,b.l),min(a.r,b.r));
}
int n,m;
Point a[MAXN];
Limits b[MAXM];
int main(void){
n=read();
for(reg int i=1;i<=n;++i)
a[i].x=read(),a[i].y=read(),a[i].v=readll();
m=read();
for(reg int i=1;i<=m;++i){
do
b[i].ch=getchar();
while(!isalpha(b[i].ch));
b[i].a=read(),b[i].b=read();
}
reg ll ans=0;
for(reg int k=1;k<=n;++k){
static Interval invx[MAXN],invy[MAXN];
fill(invx+1,invx+k+1,Interval(-inf,inf));
fill(invy+1,invy+k+1,Interval(-inf,inf));
for(reg int i=1;i<=m;++i){
switch(b[i].ch){
case 'L':{
for(reg int j=b[i].b+1;j<=k;++j)
invx[j]=cap(invx[j],Interval(b[i].a+1,inf));
break;
}
case 'R':{
for(reg int j=1;j<=k-b[i].b;++j)
invx[j]=cap(invx[j],Interval(-inf,b[i].a-1));
break;
}
case 'D':{
for(reg int j=b[i].b+1;j<=k;++j)
invy[j]=cap(invy[j],Interval(b[i].a+1,inf));
break;
}
case 'U':{
for(reg int j=1;j<=k-b[i].b;++j)
invy[j]=cap(invy[j],Interval(-inf,b[i].a-1));
break;
}
}
}
reg int s=0,t=2*k+2*n+1;
Network::init(s,t);
for(reg int i=1;i<=k;++i){
Network::Add_Tube(s,i,1,0);
Network::Add_Tube(k+n+n+i,t,1,0);
}
for(reg int i=1;i<=n;++i)
Network::Add_Tube(k+i,k+n+i,1,-a[i].v);
for(reg int i=1;i<=k;++i)
for(reg int j=1;j<=n;++j){
if(invx[i].in(a[j].x))
Network::Add_Tube(i,k+j,1,0);
if(invy[i].in(a[j].y))
Network::Add_Tube(k+n+j,k+n+n+i,1,0);
}
pair<int,ll> res=Network::dinic(s,t);
if(res.first==k)
ans=max(ans,-res.second);
}
printf("%lld\n",ans);
return 0;
}
标签:Phantom,return,int,题解,ll,dis,agc031,reg,珠宝 来源: https://www.cnblogs.com/Lu-Anlai/p/14838752.html