Python数据分析：常见的数据预处理方法

本文的文字及图片来源于网络,仅供学习、交流使用,不具有任何商业用途,如有问题请及时联系我们以作处理。

以下文章来源于数据杂论，作者：Wpc7113

 

Python 数据分析入门案例讲解

https://www.bilibili.com/video/BV18f4y1i7q9/

 

1.标准化：去均值，方差规模化

Standardization标准化:将特征数据的分布调整成标准正态分布，也叫高斯分布，也就是使得数据的均值为0，方差为1.

标准化的原因在于如果有些特征的方差过大，则会主导目标函数从而使参数估计器无法正确地去学习其他特征。

标准化的过程为两步：去均值的中心化（均值变为0）；方差的规模化（方差变为1）。

from sklearn import preprocessing
from sklearn.datasets import load_iris
iris = load_iris()
X, y = iris.data, iris.target
'''标准变换'''
scaler = preprocessing.StandardScaler().fit(X)
x_scaler=scaler.transform(X)

 

2. 最小-最大规范化

最小-最大规范化对原始数据进行线性变换，变换到[0,1]区间（也可以是其他固定最小最大值的区间）

min_max_scaler = preprocessing.MinMaxScaler()
x_train_minmax = min_max_scaler.fit_transform(X)

 

3.MaxAbsScaler

max_abs_scaler = preprocessing.MaxAbsScaler()
x_train_maxabs = max_abs_scaler.fit_transform(X)

 

4.RobustScaler：带有outlier的数据的标准化

transformer = preprocessing.RobustScaler().fit(X)
x_robust_scaler=transformer.transform(X)

 

5.QuantileTransformer 分位数变换

quantile_transformer = preprocessing.QuantileTransformer(random_state=0)
X_train_trans = quantile_transformer.fit_transform(X)

 

6.Box-Cox

Box-Cox变换是Box和Cox在1964年提出的一种广义幂变换方法，是统计建模中常用的一种数据变换，用于连续的响应变量不满足正态分布的情况。Box-Cox变换之后，可以一定程度上减小不可观测的误差和预测变量的相关性。Box-Cox变换的主要特点是引入一个参数，通过数据本身估计该参数进而确定应采取的数据变换形式，Box-Cox变换可以明显地改善数据的正态性、对称性和方差相等性，对许多实际数据都是行之有效。变化方式如下：

 

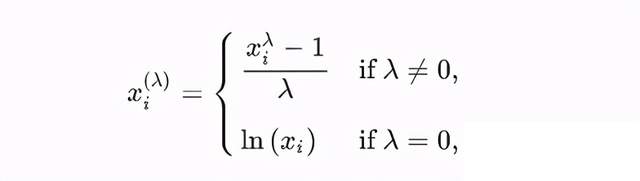
pt = preprocessing.PowerTransformer(method='box-cox', standardize=False)
pt.fit_transform(X)

 

 

7.规范化（Normalization）

规范化是将不同变化范围的值映射到相同的固定范围，常见的是[0,1]，此时也称为归一化。

X_normalized = preprocessing.normalize(X, norm='l2')

 

8.独热编码

enc = preprocessing.OneHotEncoder(categories='auto')
enc.fit(y.reshape(-1,1))
y_one_hot=enc.transform(y.reshape(-1,1))
y_one_hot.toarray()

 

9.Binarizer二值化

binarizer = preprocessing.Binarizer(threshold=1.1)
binarizer.fit(X)
binarizer.transform(X)

 

10.多项式变换

poly =preprocessing.PolynomialFeatures(2)
poly.fit_transform(X)

 

11.自定义变换

transformer = preprocessing.FunctionTransformer(np.log1p, validate=True)
transformer.fit(X)
log1p_x=transformer.transform(X)

 

标签：数据分析,transformer,scaler,fit,Python,transform,变换,preprocessing,预处理
来源： https://www.cnblogs.com/hhh188764/p/14154570.html