首页 > 编程语言> > R语言stan概率编程规划简介

R语言stan概率编程规划简介

2019-06-12 21:52:16 作者：互联网

概率编程使我们能够实现统计模型，而无需担心技术细节。它对基于MCMC采样的贝叶斯模型特别有用。在本文中，我将研究如何通过在R 。

简介

RStan是贝叶斯推理的C ++库。它基于No-U-Turn采样器（NUTS），用于根据用户指定的模型和数据估计后验分布。使用Stan执行分析涉及以下步骤：

使用Stan建模语言指定统计模型。这通常通过专用的.stan文件完成。
准备要输入模型的数据。
使用该stan函数从后验分布中取样。
分析结果。

在本文中，我将展示Stan使用两个分层模型的用法。我将使用第一个模型来讨论Stan的基本功能，并使用第二个示例来演示更高级的应用程序。

数据集

该数据集测量了教练计划对大学入学考试的影响，即美国使用的学术能力倾向测验（SAT）。SAT的设计应该能够抵抗直接针对提高测试成绩的短期努力。相反，测试应反映在较长时间内获得的知识。数据集如下：

学校	教练的估计效果（ÿĴÿĴ）	标准效果误差（σĴσĴ）
a	28	15
b	8	10
C	-3	16
d	7	11
e	-1	9
f	1	11
g	18	10
h	12	18

正如我们所看到的，国家税务总局没有履行承诺：对于八所学校中的大多数，短期教练确实增加了SAT成绩，正如 ÿĴÿĴ，哪里 ÿĴÿĴ表示SAT分数的变化。对于此数据集，我们有兴趣估计与每所学校相关的真实效果大小。可以使用两种替代方法。首先，我们可以假设所有学校都是相互独立的。然而，这将导致难以解释的估计，因为由于高标准误差，学校的95％后验间隔将在很大程度上重叠。其次，人们可以汇集所有学校的数据，假设所有学校的真实效果相同。然而，这也是不合理的，因为应该有针对学校的影响（例如不同的教师和学生）。

因此，需要另一种模型。分层模型的优点是结合了所有八所学校（实验）的信息，而没有假设它们具有共同的真实效果。我们可以通过以下方式指定层次贝叶斯模型

根据该模型，教练的效果遵循正态分布，其均值是真实效果， θĴθĴ，其标准差是 σĴσĴ，从数据中已知。真正的效果，θĴθĴ，遵循带参数的正态分布 μμ 和 ττ。

定义Stan模型文件

指定了我们将要使用的模型后，我们现在可以考虑如何在Stan中指定此模型。在为上面指定的模型定义Stan程序之前，让我们先看看Stan建模语言的结构。

变量

在Stan中，变量可以通过以下方式定义：

int<lower=0> n; # lower bound is 0
int<upper=5> n; # upper bound is 5
int<lower=0,upper=5> n; # n is in [0,5]

注意，如果它们是先验已知的，则应指定变量的上边界和下边界。

可以通过方括号指定多维数据：

vector[n] numbers; // a vector of length n
real[n] numbers;  // an array of floats with length n
matrix[n,n] matrix; // an n times n matrix

程序块

Stan中使用了以下程序块：

data：用于指定使用Bayes规则的条件
转换数据：用于预处理数据
参数（必需）：用于指定模型的参数
变换后的参数：用于计算后验之前的参数处理
model（必需）：用于指定模型本身
生成数量：用于后处理结果

对于模型程序块，可以以两种等效方式指定分布。第一个，使用以下统计表示法：

y ~ normal(mu, sigma); # y follows a normal distribution

第二种方法使用基于对数概率密度函数（lpdf）的编程表示法：

target += normal_lpdf(y | mu, sigma); # increment the normal log density

Stan支持大量的概率分布。通过Stan指定模型时，该lookup功能派上用场：它提供了从R功能到Stan功能的映射。请考虑以下示例：

##     StanFunction             Arguments ReturnType Page
## 355   normal_rng (real mu, real sigma)       real  494

在这里，我们看到rnormR 中的等价物是normal_rngStan。

八所学校的模型

现在我们已经了解了Stan建模langeu的基础知识，我们可以定义我们的模型，我们将它存储在一个名为的文件中schools.stan：

data {
  int<lower=0> n; //number of schools
 
}
parameters {

  vector[n] eta; // standardized school-level effects (see below)
}
transformed parameters {
}
model {
}

注意 θθ从未出现在参数中。这是因为我们没有明确建模θθ 而是模特 ηη，个别学校的标准化效果。然后我们构建θθ在变换后的参数部分中μμ， ττ，和 ηη。此参数化使采样器更有效。

请注意，模型是使用矢量符号指定的，因为两者都是 θθ 和 σσ表明向量。这样可以改善运行时间，因为不需要遍历每个单独的元素。

准备数据进行建模

在我们拟合模型之前，我们需要将输入数据编码为一个列表，其参数应该与Stan模型的数据部分中的条目相对应。对于学校数据，数据如下：

从后验分布中取样

我们可以使用stan函数从后验分布中进行采样，执行以下三个步骤：

它将模型规范转换为C ++代码。
它将C ++代码编译为共享对象。
它根据指定的模型，数据和设置从后验分布中进行采样。

如果rstan_options(auto_write = TRUE)已在活动R会话中执行，则相同模型的后续调用将比第一次调用快得多，因为该stan函数然后跳过前两个步骤（转换和编译模型）。此外，我们将设置要使用的核心数：

现在，我们可以从后验编译模型和样本。唯一需要的两个参数stan是模型文件的位置和要输入模型的数据。此处显示的其他参数仅用于提供可能选项的概述：

模型解释

我们将首先对模型进行基本解释，然后研究MCMC程序。

基本模型解释

要使用拟合模型进行推理，我们可以使用该print函数。

## Inference for Stan model: schools.
## 4 chains, each with iter=2000; warmup=1000; thin=1; 
## post-warmup draws per chain=1000, total post-warmup draws=4000.
## 
##            mean se_mean   sd   2.5%    25%    50%    75%  97.5% n_eff Rhat
## mu         7.67    0.15 5.14  -2.69   4.42   7.83  10.93  17.87  1185    1
## tau        6.54    0.16 5.40   0.31   2.52   5.28   9.05  20.30  1157    1
## eta[1]     0.42    0.01 0.92  -1.47  -0.18   0.44   1.03   2.18  4000    1
## eta[2]     0.03    0.01 0.87  -1.74  -0.54   0.03   0.58   1.72  4000    1
## eta[3]    -0.18    0.02 0.92  -1.95  -0.81  -0.20   0.45   1.65  3690    1
## eta[4]    -0.03    0.01 0.92  -1.85  -0.64  -0.02   0.57   1.81  4000    1
## eta[5]    -0.33    0.01 0.86  -2.05  -0.89  -0.34   0.22   1.43  3318    1
## eta[6]    -0.20    0.01 0.87  -1.91  -0.80  -0.21   0.36   1.51  4000    1
## eta[7]     0.37    0.02 0.87  -1.37  -0.23   0.37   0.96   2.02  3017    1
## eta[8]     0.05    0.01 0.92  -1.77  -0.55   0.05   0.69   1.88  4000    1
## theta[1]  11.39    0.15 8.09  -2.21   6.14  10.30  15.56  30.22  2759    1
## theta[2]   7.92    0.10 6.25  -4.75   4.04   8.03  11.83  20.05  4000    1
## theta[3]   6.22    0.14 7.83 -11.41   2.03   6.64  10.80  20.97  3043    1
## theta[4]   7.58    0.10 6.54  -5.93   3.54   7.60  11.66  20.90  4000    1
## theta[5]   5.14    0.10 6.30  -8.68   1.40   5.63   9.50  16.12  4000    1
## theta[6]   6.08    0.10 6.62  -8.06   2.21   6.45  10.35  18.53  4000    1
## theta[7]  10.60    0.11 6.70  -0.94   6.15  10.01  14.48  25.75  4000    1
## theta[8]   8.19    0.14 8.18  -8.13   3.59   8.01  12.48  25.84  3361    1
## lp__     -39.47    0.07 2.58 -45.21 -41.01 -39.28 -37.70 -34.99  1251    1
## 
## Samples were drawn using NUTS(diag_e) at Thu Nov 29 11:17:50 2018.
## For each parameter, n_eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor on split chains (at 
## convergence, Rhat=1).

这里，行名称表示估计的参数：mu是后验分布的均值，tau是其标准偏差。eta和theta的条目表示向量的估计ηη 和 θθ，分别。该LP条目显示日志密度，这通常是不相关的。列指示计算的值。百分比表示可信区间。例如，教练整体效果的95％可信区间，μμ是的 [ - 1.27 ，18.26 ][- 1.27，18.26]。由于我们不太确定平均值，95％的可信区间为θĴθĴ也很宽。例如，对于第一所学校，95％的可信区间是[ - 2.19 ，32.33 ][- 2.19，32.33]。

我们可以使用plot函数可视化估算中的不确定性：

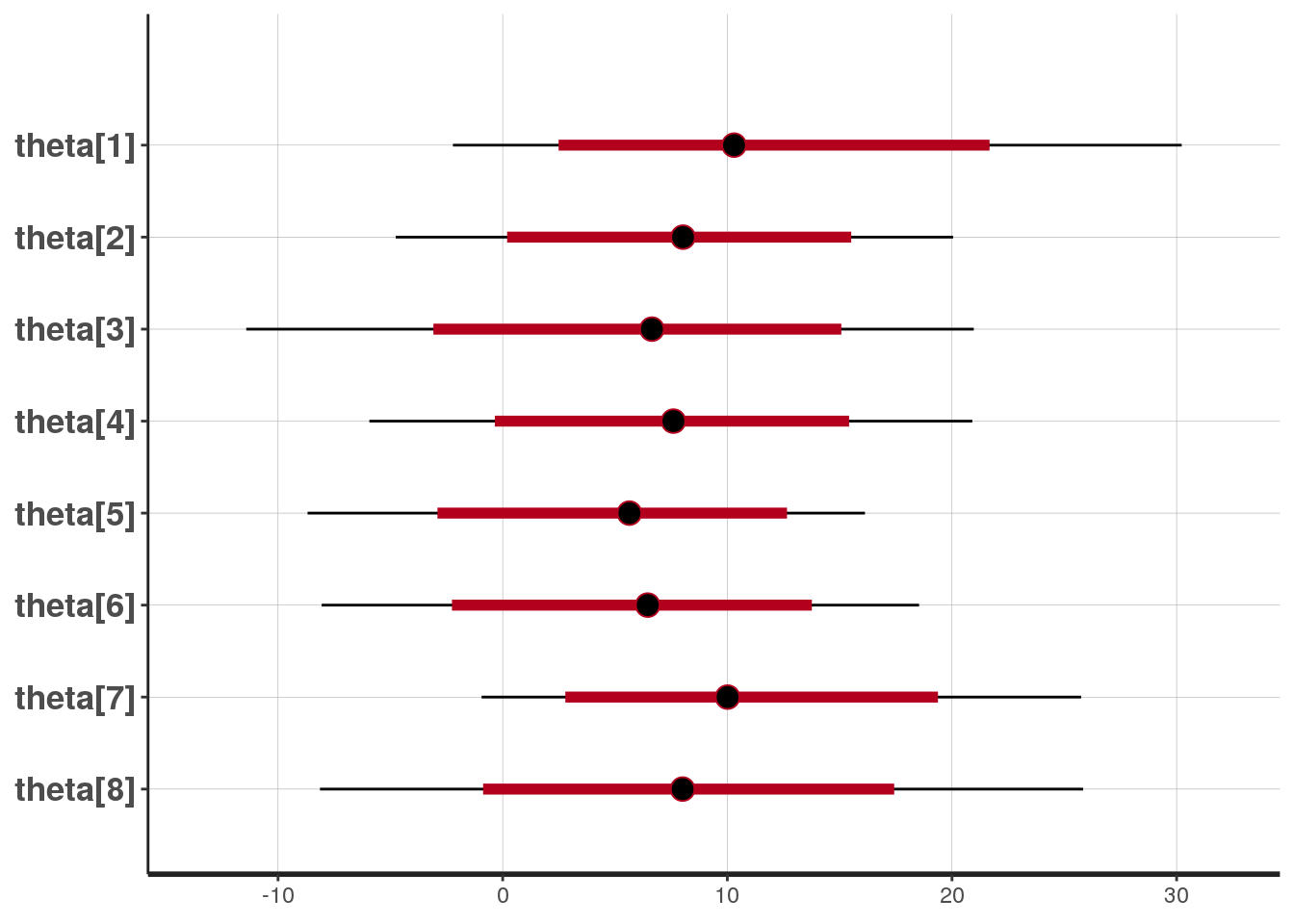
黑线表示95％的间隔，而红线表示80％的间隔。圆圈表示平均值的估计值。

我们可以使用以下extract函数获取生成的样本：

MCMC诊断

通过绘制采样程序的轨迹，我们可以确定采样过程中是否出现任何问题。例如，如果链条在一个地方停留太长时间或在一个方向上形成太多步骤，则可能是这种情况。我们可以使用traceplot函数绘制模型中使用的四条链的痕迹：

<span style="color:#000000"><span style="color:#000000"><code><span style="color:#888888"># diagnostics:</span>
traceplot(fit1, pars = c(<span style="color:#880000">"mu"</span>, <span style="color:#880000">"tau"</span>), inc_warmup = <span style="color:#78a960">TRUE</span>, nrow = <span style="color:#880000">2</span>)</code></span></span>

两条痕迹对我来说都很好。

为了从单个马尔可夫链获得样本，我们可以extract再次使用该函数：

##          parameters
## chains           mu       tau     eta[1]     eta[2]     eta[3]     eta[4]
##   chain:1  1.111120  2.729124 -0.1581242 -0.8498898  0.5025965 -1.9874554
##   chain:2  3.633421  2.588945  1.2058772 -1.1173221  1.4830778  0.4838649
##   chain:3 13.793056  3.144159  0.6023924 -1.1188243 -1.2393491 -0.6118482
##   chain:4  3.673380 13.889267 -0.0869434  1.1900236 -0.0378830 -0.2687284
##          parameters
## chains        eta[5]     eta[6]     eta[7]      eta[8]   theta[1]
##   chain:1  0.3367602 -1.1940843  0.5834020 -0.08371249  0.6795797
##   chain:2 -1.8057252  0.7429594  0.9517675  0.55907356  6.7553706
##   chain:3 -1.5867789  0.6334288 -0.4613463 -1.44533007 15.6870727
##   chain:4  0.1028605  0.3481214  0.9264762  0.45331024  2.4657999
##          parameters
## chains     theta[2] theta[3]    theta[4]  theta[5]  theta[6]  theta[7]
##   chain:1 -1.208335 2.482769 -4.31289292  2.030181 -2.147684  2.703297
##   chain:2  0.740736 7.473028  4.88612054 -1.041502  5.556902  6.097494
##   chain:3 10.275294 9.896345 11.86930758  8.803971 15.784656 12.342510
##   chain:4 20.201935 3.147213 -0.05906019  5.102037  8.508530 16.541455
##          parameters
## chains     theta[8]      lp__
##   chain:1 0.8826584 -41.21499
##   chain:2 5.0808317 -41.17178
##   chain:3 9.2487083 -40.35351
##   chain:4 9.9695268 -36.34043

为了对采样过程进行更高级的分析，我们可以使用shinystan提供Shiny前端的包。使用该软件包，可以通过以下方式启动Shiny应用程序来分析拟合模型：

分层回归

现在我们对Stan有了基本的了解，我们可以深入了解更高级的应用程序：让我们尝试分层回归。在传统的回归中，我们模拟了形式的关系

ÿ= β0+ X.β。ÿ=β0+Xβ。

该表示假定所有样本具有相同的分布。如果存在一组样本，那么我们就会遇到问题，因为组内和组之间的潜在差异将被忽略。

另一种方法是为每个组建立一个回归模型。然而，在这种情况下，在估计单个模型时，小样本量将是有问题的。

分层回归是两个极端之间的折衷。该模型假设这些组相似但仍然表现出差异。

假设每个样本属于其中一个 ķķ组。然后，分层回归指定如下：

ÿķ= αķ+ X.ķβ（k ），∀ ķ ∈ { 1 ，... ，ķ}ÿķ=αķ+Xķβ（ķ），∀ķ∈{1，...，ķ}

哪里 ÿķÿķ 是结果 ķķ- 小组， αķαķ 是拦截， XķXķ 是功能，和 β（k ）β（ķ）表示权重。层次模型与模型不同ÿķÿķ 因为参数适合每个组， αķαķ 和 β（k ）β（ķ）假定来自共同分布。

大鼠数据集

分层回归的典型示例是大鼠数据集。该纵向数据集包含测量5周的大鼠重量。让我们加载数据：

##   day8 day15 day22 day29 day36
## 1  151   199   246   283   320
## 2  145   199   249   293   354
## 3  147   214   263   312   328
## 4  155   200   237   272   297
## 5  135   188   230   280   323
## 6  159   210   252   298   331

数据显示出不同大鼠的线性增长趋势非常相似。然而，我们也看到大鼠具有不同的初始重量，这需要不同的截距，以及不同的生长速率，这需要不同的斜率。因此，分层模型似乎是合适的。

分层回归模型的规范

我们现在可以指定模型并将其存储在一个名为的文件中rats.stan：

data {
    int<lower=0> N; // the number of rats
    int<lower=0> T; // the number of time points
     real y[N,T]; // matrix of weight times time
    real xbar; // the median number of days in the time series
}
parameters {
  real alpha[N]; // the intercepts of rat weights
 
  real mu_alpha; // the mean intercept
  real mu_beta; // the mean slope

  real<lower=0> sigmasq_y;
  real<lower=0> sigmasq_alpha;
 }
transformed parameters {
  real<lower=0> sigma_y; // sd of rat weight
  real<lower=0> sigma_alpha; // sd of intercept distribution
 
  sigma_y <- sqrt(sigmasq_y);
  sigma_alpha <- sqrt(sigmasq_alpha);
  sigma_beta <- sqrt(sigmasq_beta);
}
model {
  mu_alpha ~ normal(0, 100); // non-informative prior
  mu_beta ~ normal(0, 100); // non-informative prior
   sigmasq_alpha ~ inv_gamma(0.001, 0.001); // conjugate prior of normal
  sigmasq_beta ~ inv_gamma(0.001, 0.001); // conjugate prior of normal
   for (n in 1:N) // for each sample
    for (t in 1:T)  // for each time point
      y[n,t] ~ normal(alpha[n] + beta[n] * (x[t] - xbar), sigma_y);

}
generated quantities {
  // determine the intercept at time 0 (birth weight)
   alpha0 <- mu_alpha - xbar * mu_beta;
}

请注意，模型代码估计方差（sigmasq变量）而不是标准偏差。此外，生成的数量块显式计算α0α0，时间0的截距，即出生时大鼠的体重。我们还可以计算生成量块中的任何其他数量，例如，不同时间点的大鼠的估计重量。我们稍后会在R中执行此操作。

数据准备

要为模型准备数据，我们首先将测量点提取为数值，然后在列表结构中对所有内容进行编码：

拟合回归模型

我们现在可以拟合大鼠体重数据集的贝叶斯分层回归模型：

用层次回归模型预测

确定了 αα 和 ββ对于每只大鼠，我们现在可以在任意时间点估计个体大鼠的体重。在这里，我们感兴趣的是从第0天到第100天找到大鼠的体重。

与原始数据相比，模型的估计是平滑的，因为每条曲线都遵循线性模型。研究最后一个图中显示的置信区间，我们可以看出方差估计是合理的。我们对采样时的大鼠重量（第8天到第36天）充满信心，但随着我们离采样区域越远，不确定性越大。

如果您有任何疑问，请在下面发表评论。

标签：chain,##,简介,模型,编程,Stan,eta,stan,theta
来源： https://blog.csdn.net/qq_19600291/article/details/89888740