数据结构——图的遍历算法
作者:互联网
图的遍历算法
上一篇我们了解了图的基本概念、术语以及存储结构,还对邻接表结构进行了模拟实现。本篇我们来了解一下图的遍历,和树的遍历类似,从图的某一顶点出发访问图中其余顶点,并且使每一个顶点仅被访问一次,这一过程就叫做图的遍历(Traversing Graph)。如果只访问图的顶点而不关注边的信息,那么图的遍历十分简单,使用一个foreach语句遍历存放顶点信息的数组即可。但是,如果为了实现特定算法,就必须要根据边的信息按照一定的顺序进行遍历。图的遍历算法是求解图的连通性问题、拓扑排序和求解关键路径等算法的基础。
一、图的遍历
图的遍历要比树的遍历复杂得多,由于图的任一顶点都可能和其余顶点相邻接,所以在访问了某顶点之后,可能顺着某条边又访问到了已访问过的顶点。因此,在图的遍历过程中,必须记下每个访问过的顶点,以免同一个顶点被访问多次。为此,给顶点附加一个访问标志isVisited,其初值为false,一旦某个顶点被访问,则将其isVisited标志设为true。
protected class Vertex<TValue>
{
public TValue data; // 数据
public Node firstEdge; // 邻接点链表头指针
public bool isVisited; // 访问标志:遍历时使用
public Vertex()
{
this.data = default(TValue);
}
public Vertex(TValue value)
{
this.data = value;
}
}
在上面的顶点类的定义中,增加了一个bool类型的成员isVisited,用于在遍历时判断是否已经访问过了该顶点。一般在进行遍历操作时,会首先将所有顶点的isVisited属性置为false,于是可以写一个辅助方法InitVisited(),如下所示:
/// <summary>
/// 辅助方法:初始化顶点的visited标志为false
/// </summary>
private void InitVisited()
{
foreach (Vertex<T> v in items)
{
v.isVisited = false;
}
}
图的遍历方法主要有两种:一种是深度优先搜索遍历(Depth-First Search,DFS),另一种是广度优先搜索遍历(Breadth-First Search,BFS)。下面,我们就来仔细看看这两种图的遍历算法。
二、深度优先搜索遍历
2.1 深度优先遍历原理
图的深度优先遍历类似于二叉树的深度优先遍历,其基本思想是:从图中某个顶点v出发,访问此顶点,然后从v的未被访问的邻接点出发深度优先遍历图,直至图中所有和v有路径相通的顶点都被访问到。显然,这是一个递归的搜索过程。
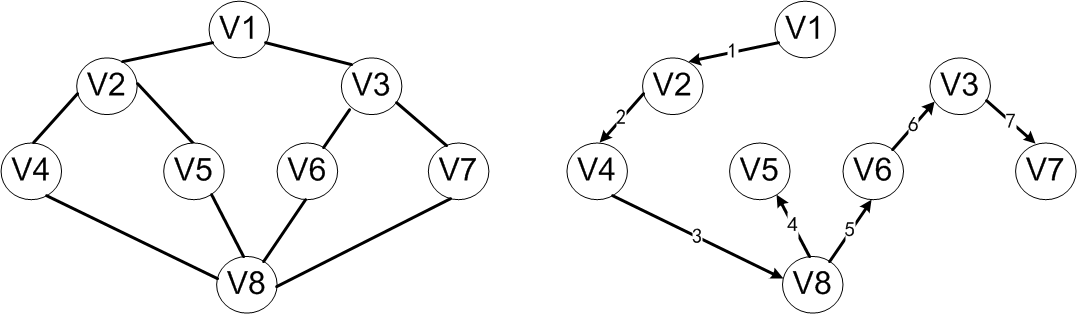
以上图为例,假定V1是出发点,首先访问V1。这时两个邻接点V2、V3均未被访问,可以选择V2作为新的出发点,访问V2之后,再找到V2的未访问过的邻接点。同V2邻接的有V1、V4和V5,其中V1已经访问过了,可以选择V4作为新的出发点。重复上述搜索过程,继续依次访问V8、V5。访问V5之后,由于与V5相邻的顶点均已被访问过,搜索退回到V8,访问V8的另一个邻接点V6.接下来依次访问V3和V7,最后得到的访问序列为V1→V2→V4→V8→V5→V6→V3→V7。
2.2 深度优先遍历实现
(1)实现代码
/// <summary>
/// 深度优先遍历接口For连通图
/// </summary>
public void DFSTraverse()
{
InitVisited(); // 首先初始化visited标志
DFS(items[0]); // 从第一个顶点开始遍历
}
/// <summary>
/// 深度优先遍历算法
/// </summary>
/// <param name="v">顶点</param>
private void DFS(Vertex<T> v)
{
v.isVisited = true; // 首先将访问标志设为true标识为已访问
Console.Write(v.data.ToString() + " "); // 进行访问操作:这里是输出顶点data
Node node = v.firstEdge;
while (node != null)
{
if (node.adjvex.isVisited == false) // 如果邻接顶点未被访问
{
DFS(node.adjvex); // 递归访问node的邻接顶点
}
node = node.next; // 访问下一个邻接点
}
}
深度优先遍历是一个典型的递归过程,这里也使用了递归的方式。
(2)遍历测试
这里的测试代码构造的图如下所示:

测试代码如下所示:

static void MyAdjacencyListDFSTraverseTest()
{
Console.Write("深度优先遍历:");
MyAdjacencyList<string> adjList = new MyAdjacencyList<string>();
// 添加顶点
adjList.AddVertex("V1");
adjList.AddVertex("V2");
adjList.AddVertex("V3");
adjList.AddVertex("V4");
adjList.AddVertex("V5");
adjList.AddVertex("V6");
adjList.AddVertex("V7");
adjList.AddVertex("V8");
// 添加边
adjList.AddEdge("V1", "V2");
adjList.AddEdge("V1", "V3");
adjList.AddEdge("V2", "V4");
adjList.AddEdge("V2", "V5");
adjList.AddEdge("V3", "V6");
adjList.AddEdge("V3", "V7");
adjList.AddEdge("V4", "V8");
adjList.AddEdge("V5", "V8");
adjList.AddEdge("V6", "V8");
adjList.AddEdge("V7", "V8");
// DFS遍历
adjList.DFSTraverse();
Console.WriteLine();
}
View Code
运行结果如下图所示:

三、广度优先搜索遍历
3.1 广度优先遍历原理
图的广度优先遍历算法是一个分层遍历的过程,和二叉树的广度优先遍历类似,其基本思想在于:从图中的某一个顶点Vi触发,访问此顶点后,依次访问Vi的各个为层访问过的邻接点,然后分别从这些邻接点出发,直至图中所有顶点都被访问到。
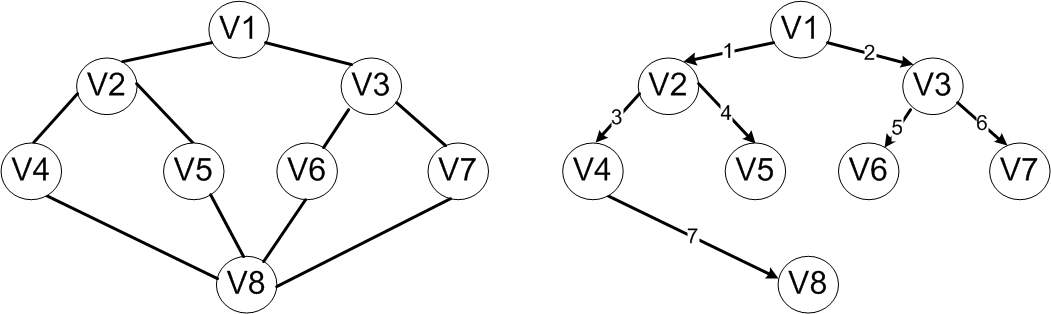
对于上图所示的无向连通图,若从顶点V1开始,则广度优先遍历的顶点访问顺序是V1→V2→V3→V4→V5→V6→V7→V8。
3.2 广度优先遍历实现
(1)实现代码
/// <summary>
/// 宽度优先遍历接口For连通图
/// </summary>
public void BFSTraverse()
{
InitVisited(); // 首先初始化visited标志
BFS(items[0]); // 从第一个顶点开始遍历
}
/// <summary>
/// 宽度优先遍历算法
/// </summary>
/// <param name="v">顶点</param>
private void BFS(Vertex<T> v)
{
v.isVisited = true; // 首先将访问标志设为true标识为已访问
Console.Write(v.data.ToString() + " "); // 进行访问操作:这里是输出顶点data
Queue<Vertex<T>> verQueue = new Queue<Vertex<T>>(); // 使用队列存储
verQueue.Enqueue(v);
while (verQueue.Count > 0)
{
Vertex<T> w = verQueue.Dequeue();
Node node = w.firstEdge;
// 访问此顶点的所有邻接节点
while (node != null)
{
// 如果邻接节点没有被访问过则访问它的边
if (node.adjvex.isVisited == false)
{
node.adjvex.isVisited = true; // 设置为已访问
Console.Write(node.adjvex.data + " "); // 访问
verQueue.Enqueue(node.adjvex); // 入队
}
node = node.next; // 访问下一个邻接点
}
}
}
和树的层次遍历类似,借助了队列这一数据结构进行辅助,记录顶点的邻接点。
(2)遍历测试
这里构造的图如下所示,跟上面原理中的图一致:

测试代码如下所示:

static void MyAdjacencyListTraverseTest()
{
MyAdjacencyList<string> adjList = new MyAdjacencyList<string>();
// 添加顶点
adjList.AddVertex("V1");
adjList.AddVertex("V2");
adjList.AddVertex("V3");
adjList.AddVertex("V4");
adjList.AddVertex("V5");
adjList.AddVertex("V6");
adjList.AddVertex("V7");
adjList.AddVertex("V8");
// 添加边
adjList.AddEdge("V1", "V2");
adjList.AddEdge("V1", "V3");
adjList.AddEdge("V2", "V4");
adjList.AddEdge("V2", "V5");
adjList.AddEdge("V3", "V6");
adjList.AddEdge("V3", "V7");
adjList.AddEdge("V4", "V8");
adjList.AddEdge("V5", "V8");
adjList.AddEdge("V6", "V8");
adjList.AddEdge("V7", "V8");
Console.Write("广度优先遍历:");
// BFS遍历
adjList.BFSTraverse();
Console.WriteLine();
}
View Code
运行结果如下图所示:

四、非连通图的遍历
以上讨论的图的两种遍历方法都是针对无向连通图的,它们都是从一个顶点触发就能访问到图中的所有顶点。若无方向图是非连通图,则只能访问到初始点所在连通分量中的所有顶点,其他分量中的顶点是无法访问到的。如下图所示,V6、V7以及V8三个顶点均访问不到。为此,需要从其他每个连通分量中选择初始点,分别进行遍历,才能够访问到图中的所有顶点。
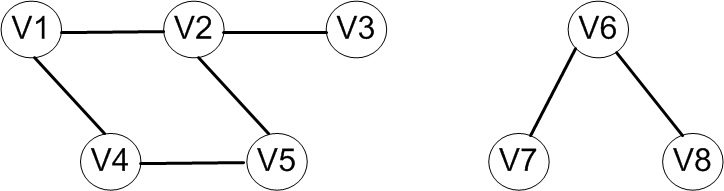
4.1 非连通图的深度优先遍历实现
/// <summary>
/// 深度优先遍历接口For非联通图
/// </summary>
public void DFSTraverse4NUG()
{
InitVisited();
foreach (var v in items)
{
if (v.isVisited == false)
{
DFS(v);
}
}
}
这里DFS方法跟上面无向连通图的保持一致。
4.2 非连通图的广度优先遍历实现
/// <summary>
/// 广度优先遍历接口For非联通图
/// </summary>
public void BFSTraverse4NUG()
{
InitVisited();
foreach (var v in items)
{
if (v.isVisited == false)
{
BFS(v);
}
}
}
这里BFS方法跟上面无向连通图的保持一致。
4.3 非连通图的遍历测试
构造的图如上图所示,测试代码如下:

static void MyAdjacencyListTraverseTest()
{
Console.WriteLine("------------非连通图的遍历------------");
MyAdjacencyList<string> numAdjList = new MyAdjacencyList<string>();
// 添加顶点
numAdjList.AddVertex("V1");
numAdjList.AddVertex("V2");
numAdjList.AddVertex("V3");
numAdjList.AddVertex("V4");
numAdjList.AddVertex("V5");
numAdjList.AddVertex("V6");
numAdjList.AddVertex("V7");
numAdjList.AddVertex("V8");
// 添加边
numAdjList.AddEdge("V1", "V2");
numAdjList.AddEdge("V1", "V4");
numAdjList.AddEdge("V2", "V3");
numAdjList.AddEdge("V2", "V5");
numAdjList.AddEdge("V4", "V5");
numAdjList.AddEdge("V6", "V7");
numAdjList.AddEdge("V6", "V8");
Console.Write("深度优先遍历:");
// DFS遍历
numAdjList.DFSTraverse4NUG();
Console.WriteLine();
Console.Write("广度优先遍历:");
// BFS遍历
numAdjList.BFSTraverse4NUG();
}
View Code
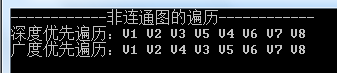
运行结果如下图所示:
作者:周旭龙
出处:http://edisonchou.cnblogs.com
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文链接。
标签:遍历,adjList,AddVertex,访问,算法,顶点,数据结构,AddEdge 来源: https://www.cnblogs.com/luanxm/p/10849742.html
