算法权衡
作者：互联网
首先，选择一个散列函数将键（字符串）映射到整数。您的哈希函数应该很快。这往往会排除像SHA-1或MD5这样的加密文件。是的，它们分布良好，但计算成本也太高——有更便宜的选择可供选择。像MurmurHash这样的东西很好，但现在有稍微好一点的。xxHash、MetroHash或SipHash1-3等非加密散列函数都是很好的替代品。
如果您有N个服务器，则使用散列函数散列密钥，并取生成的整数模值N。
服务器 := serverList[hash(key) % N]
这种设置有很多优点。首先，这很容易解释。计算起来也很便宜。模量可能很贵，但几乎可以肯定比哈希键更便宜。如果你的N是2的幂，那么你可以遮盖较低的位。（这是分割一组锁或其他内存数据结构的好方法。）
这种方法的缺点是什么？首先，如果您更改服务器数量，几乎每个密钥都会映射到其他地方。这很糟糕。
让我们考虑一下“最优”函数在这里会做什么。
- 添加或删除服务器时，只有1/n的密钥应该移动。
- 不要移动任何不需要移动的钥匙。
为了扩展第一点，如果我们从9台服务器移动到10台服务器，那么新服务器应该用所有密钥的十分之一填充。这些密钥应该从9个“旧”服务器中均匀选择。密钥只能移动到新服务器，切勿在两台旧服务器之间移动。同样，如果我们需要删除服务器（例如，因为它崩溃了），那么密钥应该均匀地分布在剩余的实时服务器上。
幸运的是，有一篇论文可以解决这个问题。1997年，论文《一致的哈希和随机树：用于缓解万维网上热点的分布式缓存协议》发布。本文描述了Akamai在其分布式内容交付网络中使用的方法。
直到2007年，这些想法才渗入大众意识。那一年出版了两部作品：
- last.fm的Ketama memcached客户端。
- Dynamo：亚马逊的高可用性键值商店
这些巩固了一致散列作为标准缩放技术的位置。它现在被Cassandra、Riak以及基本上所有其他需要在服务器上分配负载的分布式系统使用。
该算法是流行的基于环的一致散列。您可能已经看到了“圆点”图表。当您进行“一致散列”的图像搜索时，您会得到以下内容：在实践中，每个服务器在圆圈上多次出现。这些额外的点被称为“虚拟节点”或“vnodes”。这减少了服务器之间的负载差异。有了少量的vnode，可以为不同的服务器分配非常不同的密钥数量。
（关于术语的简短说明。原始的一致散列纸称为服务器“节点”。论文通常会谈论“节点”、“服务器”或“碎片”。本文将互换使用所有三个。）
环形散列的另一个好东西是，该算法是直截了当的。以下是从groupcache中提取的简单实现（为清晰起见略有修改）：
要将nodes列表添加到环形散列中，每个节点都以略微不同的名称（0 node1，1 node1，2 node1，...）进行散列m.replicas散列值被添加到m.nodes切片中，从散列值到节点的映射存储在m.hashMap。最后，对m.nodes切片进行了排序，以便我们可以在查找期间使用二进制搜索。
func (m *Map) Add(nodes ...string) {
对于 _, n := 范围节点 {
for i := 0; i < m.replicas; i++ {
哈希 := int(m.hash([]byte(strconv.Itoa(i) + " " + n)))
m.nodes = append（m.nodes，散列）
m.hashMap[hash] = n
}
}
sort.Ints（m.nodes）
}
要查看给定key存储在哪个节点上，将其哈希为整数。搜索排序的nodes切片，以找到大于键哈希的最小节点哈希值（如果我们需要绕到圆圈的开头，则使用特殊情况）。然后在地图中查找该节点散列，以确定它来自的节点。
func (m *Map) Get(key string) string {
哈希 := int(m.hash([]byte(key)))
idx := sort.Search（len（m.keys），
func(i int) bool { return m.keys[i] >= hash }
）
如果 idx == len(m.keys) {
idx = 0
}
返回m.hashMap[m.keys[idx]]
}
关于Ketama的简短题外话
Ketama是一个memcached客户端，它使用环形散列跨服务器实例分割密钥。我需要一个兼容的Go实现，并遇到了这个问题。
这行C的Go等价物是什么？
unsigned int k_limit = floorf(pct * 40.0 * ketama->numbuckets);
这是一个棘手的问题：你不能孤立地回答它。您需要知道这些类型以及C的促销规则：
浮动地板f（浮动x）； 未签名的int numbuckets； 浮动pct；
答案是：
限制 := int(float32(float64(pct) * 40.0 * float64(numbuckets)))
原因是C的算术推广规则，以及40.0常数是float64。
一旦我为我的go-ketama实现整理了这个问题，我立即编写了自己的环形散列库（libchash），它不依赖于浮点舍入误差来获得正确性。我的库也稍微快一点，因为它不使用MD5进行散列。
教训：如果您正在构建任何需要跨语言的东西，请避免隐式浮点转换，以及一般的浮点转换。
插曲结束。
“我们完成了吗？”或者“为什么这仍然是一个研究主题？”
环形散列为我们最初的问题提供了解决方案。案件结案？不完全是。环形哈希仍然有一些问题。
首先，跨节点的负载分布仍然可能不均匀。每台服务器有100个副本（“vnodes”），负载的标准差约为10%。桶大小的99%置信区间为平均负载的0.76至1.28（即总密钥/服务器数量）。这种可变性使容量规划变得棘手。将副本数量增加到每台服务器1000点，将标准差降低到~3.2%，99%的置信区间要小得多，为0.92到1.09。
这伴随着巨大的内存成本。对于1000个节点，这是4MB的数据，O（log n）搜索（对于n=1e6），所有这些都是处理器缓存丢失，即使没有其他东西竞争缓存。
跳跃哈希
2014年，谷歌发布了名为“跳跃散列”的论文《快速、最小内存、一致散列算法》。该算法实际上包含在2011年发布的Guava库中，并表明它是从C++代码库移植的。
跳跃散列解决了环形散列的两个缺点：它没有内存开销和几乎完美的密钥分配。（桶的标准差为0.000000764%，99%的置信区间为0.99999998至1.000000002）。
跳跃哈希也很快。该循环执行O（ln n）次，比O（log n）二进制搜索环形哈希的速度快，甚至由于计算完全在几个寄存器中完成，并且不支付缓存错过的开销，甚至速度也更快。
这是从github.com/dgryski/go-jump提取的代码，从论文中的C++翻译过来。该算法的工作原理是使用密钥的散列作为随机数生成器的种子。然后，它使用随机数在桶列表中“向前跳跃”，直到它从末端掉下来。它落入的最后一个桶就是结果。这篇论文对它的工作原理进行了更完整的解释，并得出了这个优化的循环。
func Hash(key uint64, numBuckets int) int32 {
var b int64 = -1
var j int64
对于j < int64（numBuckets）{
b = j
键 = 键*2862933555777941757 + 1
j = int64（float64（b+1）*
（float64（int64（1）<<31）/float64（（键>>33）+1））
}
返回int32（b）
}
Jump Hash看起来很棒。它速度快，负载均匀分配。有什么问题吗？主要限制是它只返回0..numBuckets-1范围内的整数。它不支持任意的桶名。（使用环形散列，即使两个不同的实例以不同的顺序接收其服务器列表，生成的密钥映射仍将保持不变。）考虑Jump Hash的更好方法是提供碎片编号，而不是服务器名称。其次，您只能正确添加和删除范围上端的节点。这意味着它不支持任意节点删除。您不能用它来在一组memcached实例中分发密钥，其中一个实例可能会崩溃——无法从可能的目的地列表中删除崩溃的节点。
这些结合使Jump Hash更适合数据存储应用程序，您可以使用复制来缓解节点故障。与节点权重一起使用也可能很棘手。
“我们完成了吗？”或者“为什么这仍然是一个研究主题？”(2)
环形散列提供任意的存储桶添加和删除，以高内存使用为代价，以减少负载方差。跳跃散列提供了有效的完美负载拆分，在更改碎片计数时降低了灵活性。
有没有办法在没有内存开销的情况下实现灵活的环大小调整和低方差？
多探针一致散列
谷歌的另一篇论文“多探针一致散列”（2015年）试图解决这个问题。MPCH提供O（n）空间（每个节点一个条目），以及O（1）节点的添加和删除。陷阱？查找速度变慢了。
基本想法是，节点不是多次散列和膨胀内存使用量，而是只散列一次，但键在查找时散列k次，并返回所有查询中最近的节点。k的值由所需的方差决定。对于1.05的峰值与平均值（这意味着负载最多的节点最多比平均值高5%），k为21。使用棘手的数据结构，您可以将总查找成本从O（k log n）降至仅O（k）。我的实现使用了棘手的数据结构。
作为比较点，要使Ring Hash的等效峰值与平均值比率为1.05，每个节点需要700 ln n个副本。对于100个节点，这转化为超过1兆字节的内存。
约会哈希
解决一致散列问题的另一个早期尝试被称为rendezvous散列或“最高随机权重散列”。它还于1997年首次出版。
这个想法是，您将节点和密钥一起散列，并使用提供最高散列值的节点。缺点是很难避免迭代所有节点的O（n）查找成本。
这是取自github.com/dgryski/go-rendezvous的实现。我的实现通过预散列节点和使用xorshift随机数生成器作为廉价的整数散列函数来优化多重散列。
func (r *Rendezvous) Lookup(k string) string {
khash := r.hash(k)
var midx int
var mhash = xorshiftMult64(khash ^ r.nhash[0])
对于i，nhash := range r.nhash[1:] {
如果 h := xorshiftMult64(khash ^ nhash); h > mhash {
midx = i + 1
mhash = h
}
}
返回r.nstr[midx]
}
即使认为会合散列是O（n）查找，内部循环也没有那么昂贵。根据节点的数量，它可以很容易地“足够快”。请参阅末尾的基准。
磁悬浮散列
2016年，谷歌发布了Maglev：快速可靠的软件网络负载平衡器。论文的一节描述了一种新的一致散列算法，该算法被称为“磁悬浮散列”。
与环形散列或会合散列相比，主要目标之一是查找速度和低内存使用率。该算法有效地生成了一个查找表，允许在恒定时间内找到一个节点。两个缺点是，在节点故障时生成新表很慢（本文假设后端故障很少），这也有效地限制了后端节点的最大数量。Maglev散列还旨在在添加和删除节点时实现“最小中断”，而不是最优。对于maglev作为软件负载平衡器的用例来说，这已经足够了。
该表实际上是节点的随机排列。查找会散列密钥并检查该位置的条目。这是带有小常数的O（1）（正好是哈希键的时间）。
有关表格如何构建的更深入的描述，请参阅原始论文或《晨报》上的摘要。
复制
复制是使用一致的散列为给定的密钥选择次要（或更多）节点。这既可以防止节点故障，也可以简单地作为第二个节点进行查询，以减少尾部延迟。一些策略使用全节点复制（即每个服务器有两个完整副本），而其他策略则跨服务器复制密钥。
您始终可以以可预测的方式更改密钥或密钥散列，并进行完整的第二次查找。您也需要小心，以避免复制密钥登陆同一节点。
一些算法有直接的方法来选择多个节点进行回退或复制。对于环哈希，您使用您在圆圈上传递的下一个节点；对于多探头，您可以使用下一个最接近的节点。会合，你采取下一个最高（或最低）。跳跃有点棘手，但可以做到。
像这篇文章中的所有其他内容一样，选择复制策略充满了权衡。Vladimir Smirnov在Booking.com上谈论石墨度量存储时谈到了复制策略中的一些不同的权衡。
加权主机
一致的散列算法因添加具有不同权重的服务器的简单性和有效性而异。也就是说，向一个服务器发送更多（或更少）负载，而不是向其余服务器发送负载。使用环形散列，您可以根据所需的负载缩放副本数量。这可以大大增加内存使用量。跳跃散列和多探针一致散列使用和保持其现有性能保证更棘手。您始终可以添加第二个引用原始节点的“阴影”节点，但当负载倍数不是整数时，这种方法会失败。一种方法是将所有节点计数缩放一定数量，但这会增加内存和查找时间。
磁悬浮散列通过改变表构建过程来处理权重，以便更多重加权的节点更频繁地选择查找表中的条目。
加权会合散列是一个单行修复，用于为会合添加权重：选择按-weight / math.Log(h)缩放的最高组合哈希。
负载平衡
使用一致的散列进行负载平衡似乎是一个吸引人的想法。但根据算法，这最终不会比随机分配更好，随机分配会导致不平衡分布。
幸运的是（再次来自谷歌）除了Maglev外，我们还有两种一致的负载平衡哈希方法。
第一个，从2016年开始，与有界负载一致散列。由于密钥分布在跨服务器之间，因此会检查负载，如果已经加载过重，则跳过节点。有一篇详细的帖子详细介绍了它是如何添加到Vimeo的HAProxy的，（由Yours Truly客串:)。它也可以作为独立软件包提供。
对于选择要连接到哪组后端的客户，谷歌的SRE Book概述了一种名为“确定性子设置”的算法。有关完整的详细信息，请参阅第20章“数据中心的负载平衡”中的描述。我在github.com/dgryski/go-subset上有一个快速实现。亚马逊的这篇关于“洗牌分片”的博客文章中描述了类似的方法。
负载平衡是一个巨大的话题，很容易成为它自己的书。有关两个概述，请参阅
- 负载平衡是不可能的，作者：Tyler McMullen
- 预测负载平衡：不公平但更快、更稳健，作者：Steve Gury
基准
现在你们一直在等待的东西。希望您不要只是跳到文章的底部，忽略每个一致的哈希函数所具有的所有注意事项和权衡。
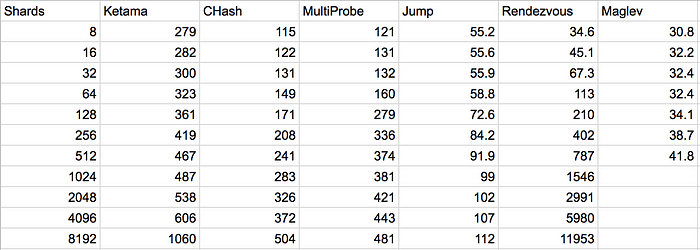具有不同节点计数的单个查找的基准；以纳秒为单位的计时
结论
如您所见，没有完美的一致哈希算法。他们都有权衡取舍。还有很多我没有在这里介绍的。但像上面一样，他们都在努力平衡分发、内存使用、查找时间和构建时间（包括节点添加和删除成本）。