用 Python 的力量释放统计学习
作者:互联网
统计学在数据科学中起着至关重要的作用。以下是统计学在数据科学领域很重要的一些关键原因:
1. 数据探索和描述:统计学为探索和描述数据提供了必不可少的工具。汇总统计量(如平均值、中位数、标准差和相关系数)有助于了解数据中的中心趋势、分布和关系。
2. 数据分析和解释:统计方法使数据科学家能够分析复杂的数据集并得出有意义的见解。回归分析、假设检验和方差分析 (ANOVA) 等技术允许识别数据中的模式、关系和显著差异。
3. 预测建模:统计学为在数据科学中构建预测模型提供了基础。线性回归、逻辑回归、决策树和时间序列分析等技术依赖于统计原理,根据历史数据进行准确的预测和预测。
4.实验设计:统计学有助于设计实验和进行假设检验。它指导样本量、随机化和对照组的选择,以确保有效和可靠的结果。统计显著性检验可以得出关于变量或干预措施影响的可信结论。
5. 数据驱动的决策:统计使数据科学家能够根据数据分析做出明智的决策。通过应用统计技术,数据科学家可以识别趋势、检测异常并量化不确定性,使组织能够做出数据驱动的选择并优化流程。
6. 特征选择和降维:统计有助于从大型数据集中识别相关特征或变量。主成分分析 (PCA)、因子分析和特征选择算法等技术利用统计方法来降低维数、提高模型性能并专注于基本信息。
7. 性能评估:统计学提供了评估机器学习模型性能的指标和方法。准确度、精密度、召回率、F1 分数和受试者工作特征 (ROC) 曲线是通常用于评估预测模型有效性和可靠性的统计度量。
8. 数据质量和验证:统计有助于评估和确保数据质量和可靠性。统计技术可以识别异常值、缺失的数据模式和数据不一致,从而实现数据清理和验证过程。
总之,统计学提供了数据科学家探索、分析、解释和从数据中获得有价值的见解所需的基本原则、技术和工具,从而实现数据驱动的决策和有效预测模型的开发。
虽然统计学是数据科学中的强大工具,但它也有一定的局限性。以下是需要考虑的一些限制:
1. 假设和简化:统计方法通常依赖于对数据的假设,例如正态性或独立性。但是,在实际场景中,数据可能并不总是满足这些假设,从而导致分析中的潜在偏差或不准确。
2. 有限的推理范围:统计学根据样本数据提供推理,以得出关于人口的结论。然而,这些推论的有效性取决于样本的代表性和质量。如果样本不真正具有代表性或存在偏差,则结果的普遍性可能会受到限制。
3. 相关性与因果关系:统计学可以识别变量之间的关系和相关性,但不能建立因果关系。相关性本身并不意味着因果关系,因为可能还有其他未观察到的因素影响变量。
4. 过拟合和欠拟合:统计模型容易出现数据过度拟合或欠拟合。当模型拟合训练数据过于接近时,就会发生过度拟合,从而导致对新数据的泛化不佳。另一方面,当模型过于简单并且无法捕获数据中的基础模式时,就会发生欠拟合。
5. 处理缺失数据:统计提供了多种处理缺失数据的方法,如插补技术。但是,这些方法引入了潜在的偏差和假设,可能会影响分析的准确性和可靠性。
6. 数据质量和异常值:统计假设数据质量高且没有异常值。但是,实际数据集通常包含错误、异常值或缺失值,这可能会影响统计分析的有效性。
7. 伦理考虑:仅靠统计学无法解决数据科学中的道德考虑。虽然统计分析可以提供见解,但基于这些见解的解释和决策需要道德判断并考虑潜在的偏见或意外后果。
8. 快速发展的数据格局:统计数据已针对传统的结构化数据进行开发和优化。然而,大数据、非结构化数据和实时流数据的兴起带来了新的挑战,这些挑战可能超出了传统统计方法的能力。
对于数据科学家来说,重要的是要意识到这些限制并适当地使用统计方法,与其他技术相辅相成,并考虑所分析数据的上下文和性质。
因此,让我们了解理解数据科学统计所需的基本内容。
在统计学中,总体、样本、参数和统计是有助于理解和分析数据的关键概念。以下是每个术语的解释:
1. 人口:人口是指具有共同兴趣特征的整个个体、物体或事件群体。它是要得出结论的一整套要素。例如,如果您正在研究一个国家/地区所有成年人的身高,则人口将由该国家/地区的每个成年人组成。
2. 样本:样本是从总体中选择的子集或较小的代表性群体。选择它是为了提供对更大人口特征的见解。样本的选择通常基于特定的抽样技术,以确保代表性。使用相同的示例,如果您随机选择并测量来自该国的 500 名成年人的身高,这 500 个人将构成您的样本。
3. 参数:参数是描述总体的数字特征或汇总度量。它们通常用希腊字母表示。参数提供有关整个总体的信息,但通常未知或难以计算,因为分析整个总体可能不可行。参数的示例包括平均身高、标准差或整个总体中某个特征的比例。
4. 统计:另一方面,统计是指从样本中计算出的数字量或度量。它们用于估计或推断总体的相应参数。统计数据以英文字母表示。例如,从样本计算的平均高度、标准差或比例将被视为统计数据。
总之,总体代表整个感兴趣组,样本是用于分析的总体子集,参数是总体的特征,统计量是从样本计算的量,用于估计或推断总体参数。总体、样本、参数和统计之间的关系是统计分析和推断的基础。
下面的代码将在 Python 中生成一个随机样本:
将 numpy 作为 np # 导入,生成以下正态分布 的人口数据 N = 10000 mu = 10 std = 2 population_df = np.random.normal( mu, std,N)# 创建随机样本 def random_sampling(df, n) 的函数: random_sample =np.random.choice(df,replace = False, size = n) return(random_sample)randomSample = random_sampling(population_df, N) randomSample

它使用 NumPy 按照均值为 10、标准差为 000 的正态分布生成大小为 10,2 的人口数据集。然后,它定义了一个名为“random_sampling”的函数,该函数将数据集“df”和样本大小“n”作为输入。此函数使用“np.random.choice”函数从数据集创建随机样本,而不进行替换,具有指定的样本大小。最后,使用“population_df”数据集和样本大小“N”调用“random_sampling”函数,样本大小与总体大小相同。这意味着整个总体被选为样本。
现在,如果我们看到并尝试匹配样本和总体,我们将看到差异
np.testing.assert_array_equal(randomSample, population_df)

但是这两个数组的平均值会给我们相同的结果。
np.testing.assert_array_equal(round(randomSample.mean(),2),round(population_df.mean(),2))
因此,这些东西作为统计学的一部分很重要,我们将主要直接处理平均值和中位数类型的元素,而不是数据本身来验证我们的假设和点。
推论和描述性统计
我需要介绍描述性统计和推论性统计之间的区别。描述性统计仅适用于从中收集数据的样本或总体的成员。相反,推论统计是指使用样本数据得出一些结论(即做出一些推论),关于样本应该代表的更大群体的特征。尽管研究人员有时对简单地描述样本的特征感兴趣,但在大多数情况下,我们更关心的是样本告诉我们的样本来自的人群。
如果样本不能真正代表总体,我们就不能确信基于我们的样本数据的结论将适用于更大的人群。这一过程中重要的第一步是明确定义样本据称代表的人群。
抽样问题
我们有不同类型的采样方法可供选择。其中一些是
- 随机抽样
- 代表性抽样
- 系统抽样
- 聚类采样
- 加权抽样
- 分层抽样
系统抽样被定义为一种概率抽样方法,其中从随机起点和固定抽样间隔后从目标总体中选择元素。
换句话说,系统抽样是概率抽样技术的扩展版本,其中定期选择组的每个成员以形成样本。我们通过将整个总体大小除以所需的样本大小来计算采样间隔。
请注意,系统抽样通常生成随机样本,但不解决所创建样本中的偏差。
下面的代码是系统采样的示例
将 numpy 导入为 NP 导入熊猫作为 PD # 生成人口数据遵循正态分布 N = 10000 mu = 10 std = 2 population_df = np.random.normal( mu, std,N) # 函数,使用系统抽样 定义systematic_sampling创建随机样本(DF,步长): ID = PD。Series(np.arange(1,len(df),1)) df = pd.Series(df) df_pd = pd.concat([id, df], axis = 1) df_pd.columns = [“id”, “data”] # 这些索引将随着步长数量而不是 1 而增加 selected_index = np.arange(1,len(df),step) # 使用 iloc 获取具有选定索引的数据 systematic_sampling = df_pd.iloc[selected_index] 返回(systematic_sampling) n = 10 步长 = int(N/n)样本 = systematic_sampling(population_df, 步长) 样本

提供的代码片段使用 NumPy 按照均值为 10、标准差为 000 的正态分布生成大小为 10,2 的人口数据集。
它定义了一个名为“systematic_sampling”的函数,该函数将数据集“df”和步长“step”作为输入。此函数执行系统采样,这是一种从有序列表中定期选择样本的方法。
在该函数中,数据集“df”被转换为熊猫系列,并创建一个额外的系列“id”来为每个数据点分配唯一标识符。然后将这两个序列连接成一个名为“df_pd”的数据框。
最后,该函数将生成的系统样本作为数据框返回。
聚类抽样是一种概率抽样技术,我们根据某些聚类标准将总体划分为多个聚类(组)。然后,我们使用简单的随机或系统抽样技术选择一个随机集群。因此,在聚类抽样中,将整个总体划分为聚类或段,然后随机选择聚类。
例如,如果您想体验评估欧洲大二学生在商业教育方面的表现。不可能在欧盟的每一所大学都进行涉及一名学生的实验。相反,通过使用聚类抽样,我们可以将每个国家的大学分组到一个聚类中。然后,这些聚类定义了欧盟的所有二年级学生群体。接下来,您可以使用简单的随机抽样或系统抽样,并随机选择聚类进行研究。
请注意,系统抽样通常生成随机样本,但不解决所创建样本中的偏差。
将 numpy 导入为 NP 导入熊猫作为 PD # 生成人口数据 price_vb = pd。Series(np.random.uniform(1,4,size = N)) id = pd.Series(np.arange(0,len(price_vb),1))event_type = pd.Series(np.random.choice([“type1”,“type2”,“type3”],size = len(price_vb)))Click = pd.Series(np.random.choice([0,1],size = len(price_vb)))df = pd.concat([id,price_vb,event_type, click],axis = 1) df.columns = [“id”,“price”,“event_type”, “click”] df

def get_clustered_Sample(df, n_per_cluster, num_select_clusters): N = len(df) K = int(N/n_per_cluster) data = None for k in range(K): sample_k = df.样本(n_per_cluster) sample_k[“集群”] = NP。Repeat(k,len(sample_k)) df = df.drop(index = sample_k.index) data = pd.concat([data,sample_k],axis = 0) random_chosen_clusters = np.random.randint(0,K,size = num_select_clusters) 样本 = data[data.cluster.isin(random_chosen_clusters)] 返回(样本)样本 = get_clustered_Sample(df = df, n_per_cluster = 100, num_select_clusters = 2) 样本

提供的代码片段定义了一个名为“get_clustered_Sample”的函数,该函数采用数据帧“df”、每个群集“n_per_cluster”所需的样本大小以及从“num_select_clusters”中选择样本的群集数作为输入。
在该函数中,计算数据帧中数据点“N”的总数。变量“K”确定为“N”的整数值除以“n_per_cluster”,表示数据中的聚类数。
循环迭代“K”次以从每个聚类中选择样本。在每次迭代中,使用“sample”函数从数据帧中随机选择一个大小为“n_per_cluster”的样本。名为“cluster”的新列将添加到示例中,并为其分配当前聚类索引“k”。然后将所选样本追加到“数据”数据帧,该数据帧最初设置为“无”。
对所有聚类进行采样后,使用“np.random.randint”随机选择聚类。“random_chosen_clusters”变量存储“num_select_clusters”随机选择的聚类索引。
最后,该函数从“数据”数据帧中选择样本,其中“聚类”列与随机选择的聚类索引匹配。生成的样本作为数据帧返回。
集中趋势的度量
如果你把一个变量的分数放在一个变量上,并按从低到高的顺序排列它们,你得到的是分数的分布。
平均值可能是所有社会科学研究中最常用的统计量。平均值只是分数分布的算术平均值,研究人员喜欢它,因为它提供了一个单一的简单数字,给出了分布的粗略摘要。重要的是要记住,尽管均值提供了有用的信息,但它并不能告诉您分数的分布程度(即方差)或分布中有多少分数接近平均值。分布在平均值或接近平均值的分数可能很少。
中位数是分布中标记第 50 个百分位数的分数。也就是说,分布中 50% 的分数高于中位数,50% 的分数低于中位数。
该模式是集中趋势度量中最少使用的,因为它提供的信息量最少。
您会注意到有两种不同的符号用于平均值和μ。需要两个不同的符号,因为区分适用于样本的统计量和应用于总体的参数非常重要。
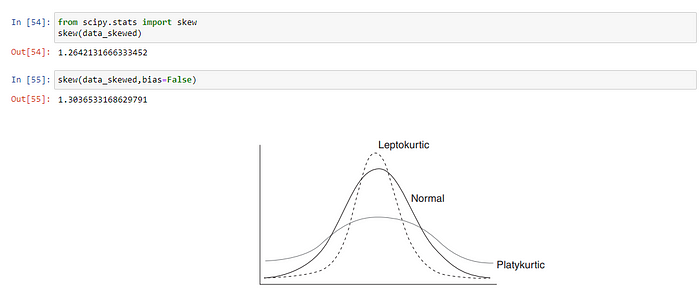
如果分布具有多个具有最常见分数的类别,则该分布具有多个模式,称为多模式。多峰分布的一个常见示例是双峰分布。
当样本中的大多数成员的分数聚集在分布的一端,而在另一端有几个分数时,则称分布是偏斜的。使用偏态分布时,均值、中位数和众数通常都位于不同的点。
有时,分布有几个分数与平均值相去甚远。这些称为异常值,并且由于根据定义,异常值是极端分数,因此它们可以对分布的平均值产生巨大影响。
数据类型
集中趋势度量的选择取决于所分析的数据类型。数据类型是指根据数据所表示的值的性质对数据进行分类。有几种类型的数据,包括名义、有序、间隔和比率数据(Mishra等人,2018)。
·名义数据是指分类数据,其中每个值代表一个单独的类别,没有内在的顺序或排名,例如性别、国籍或宗教(图 1)。
·序数数据表示具有固有排名或顺序的类别,例如教育水平或收入等级。
·区间数据表示值之间间隔相等的数值数据(值不能以小数的形式表示或表示),但没有真正的零点,例如以摄氏度或华氏度测量的温度。
·最后,比率数据表示数值数据,值与真正的零点(如体重或身高)之间的间隔相等。
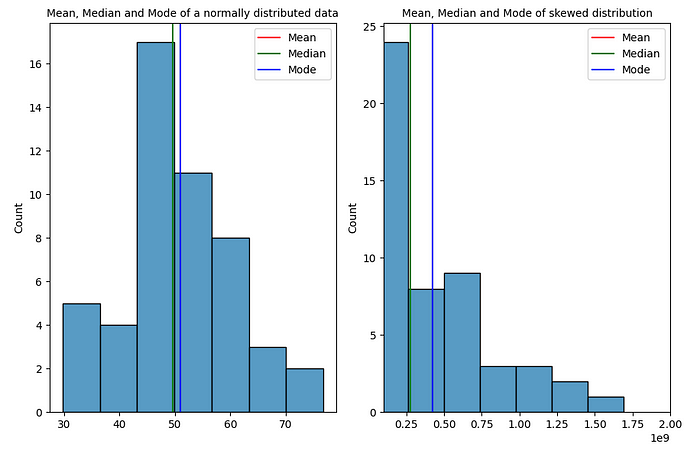
# 导入库 导入 numpy 作为 np 导入 matplotlib.pyplot 作为 plt 导入熊猫作为 pd 导入 seaborn 作为 sns # 生成一个正态分布数据集,平均值=50,标准差=10 数据 = np.random.normal (50, 10, 50) # 生成一个均值=50、标准差=10的偏斜数据集 data_skewed = np.random.normal(50, 10, 50)**5 # 计算数据集 均值 = np.均值(数据)中位数 = np.中位数(数据)模式 = np.中位数(数据) 模式 = np。round(np.mean(data))# 计算偏斜数据集的均值、中位数和众数mean_skewed = np.mean(data_skewed)median_skewed = np.median(data_skewed) mode_skewed = np。 round(np.mean(data_skewed))# 打印结果 print(“对于正态分布数据集:”)print(“Mean: ”, mean)print(“中位数: ”, median)print(“Mode: ”, mode) print(“--------------------------------------------------------------------“)print(”对于偏斜数据集:“) print(”Mean: “, mean_skewed)print(”中位数: “, median_skewed)print(”Mode: “, mode_skewed)

fig, ax= plt.subplots(1,2, figsize = (9,6))# 使用 seabron 库 绘制数据集的直方图 sns.histplot(data, ax=ax[0])ax[0].axvline(x=mean, color='r', label='Mean')ax[0].axvline(x=median, color='g', label='Median')ax[0].axvline(x=mode, color='b', label='Mode')ax[0].legend() ax[0].set_title(“Mean, Median and Mode of a 正态分布数据”, fontsize=10)sns.histplot(data_skewed, ax=ax[1])ax[1].axvline(x=mean_skewed, color='r', label='Mean')ax[1].set_xlim(100000000,2000000000) ax[1].axvline(x=median_skewed, color='g', label='Median') ax[1].axvline(x= mode_skewed, color='b', label='Mode')ax[1].set_title(“Mean, Median and Mode of Biewed distribution”, fontsize=10)ax[1].legend()plt.tight_layout()
提供的代码片段利用“matplotlib”和“seaborn”库来创建具有两个子图的图形。以下是代码的细分:“sns.histplot(data, ax=ax[0])”:这条线在第一个子图(“ax[0]”)上绘制了“data”变量的直方图。
'ax[0].axvline(x=mean, color='r', label='Mean')':这条线在 x 坐标处添加一条垂直线,等于第一个子图中 'mean' 的值。它被涂成红色并标记为“平均”。
'ax[0].axvline(x=中位数, color='g', label='中位数)':这条线在 x 坐标处添加一条垂直线,等于第一个子图中“中位数”的值。它被涂成绿色,并标记为“中位数”。
'ax[0].axvline(x=mode, color='b', label='Mode')':这条线在 x 坐标处添加一条垂直线,等于第一个子图中“mode”的值。它被涂成蓝色并标记为“模式”。
'sns.histplot(data_skewed, ax=ax[1])':这条线在第二个子图('ax[1]')上绘制了“data_skewed”变量的直方图。
'ax[1].axvline(x=mean_skewed, color='r', label='Mean')':这条线在 x 坐标处添加一条垂直线,等于第二个子图中的 'mean_skewed' 值。它被涂成红色并标记为“平均”。
'ax[1].set_xlim(100000000,2000000000)':此线将第二个子图的 x 轴限制设置为 100,000,000 到 2,000,000,000 的指定范围。
'ax[1].axvline(x=median_skewed, color='g', label='中位数)':这条线在 x 坐标处添加一条垂直线,等于第二个子图中 'median_skewed' 的值。它被涂成绿色,并标记为“中位数”。
'ax[1].axvline(x=mode_skewed, color='b', label='Mode')':这条线在 x 坐标处添加一条垂直线,等于第二个子图中的 'mode_skewed' 值。它被涂成蓝色并标记为“模式”。
总体而言,该代码生成一个包含两个子图的图形,每个子图包含一个直方图和垂直线,指示相应数据集的平均值、中位数和众数。第一个子图表示正态分布的数据集,而第二个子图表示偏态分布。
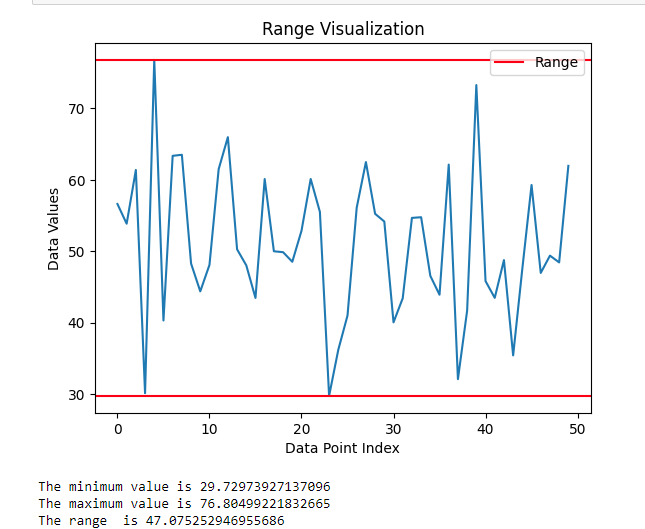
范围是最简单的离散度量,用于计算数据集中最大值和最小值之间的差异。该范围易于理解和计算,只需确定两个值(图 6)。在需要快速粗略估计变异性的情况下,该范围非常有用,并且可以提供对数据分布的一些见解。但是,该范围也有一些缺点。该范围的一个主要缺点是它对数据集中的异常值或极值高度敏感。由于范围仅基于最大值和最小值,因此异常值会对范围产生重大影响,从而导致数据分布的表示不准确。
要在 Python 中可视化数据集的范围,一种方法是创建一个简单的线图,其中两条水平线表示数据集的最小值和最大值。
方差
方差是一种统计度量,它提供一组数据中存在多少变异的定量度量。它是统计分析中广泛使用的度量,为许多统计测试和模型提供了重要的输入。使用方差的优点是它有助于理解数据的分布,并在不同的数据集之间进行有意义的比较。此外,使用统计软件可以轻松计算大型数据集的方差,这使其成为许多应用程序中使用的方便度量。此外,方差可用于识别数据中的异常值或极值,这对于检测错误或异常非常重要。但是,使用方差的一个缺点是它对异常值或极值敏感,并且可能受到它们的影响。另一个缺点是方差以原始数据的平方单位(图7)表示,对于某些应用程序来说可能不容易解释或有意义。
标准差
标准差是方差的平方根,表示数据围绕均值的分布。与方差一样,标准差可以使用统计软件轻松计算,并可用于识别数据中的异常值或极值。此外,标准差在与原始数据相同的单位中具有清晰的解释,这可以使其在某些应用中更具可解释性和意义。但是,使用标准差的一个缺点是,与方差一样,它对异常值或极值敏感,并且可能受到它们的影响。此外,标准差假定数据呈正态分布,但情况可能并非总是如此,在这种情况下,它可能无法准确表示数据中的离散。
# 计算数据集
方差的方差和标准差 = np.var(data)std_dev = np.std(data)# 创建一个直方图 plt.hist(data, bins=30, alpha=0.5)plt.axvline(x=np.mean(data), color='r', linestyle='--', label='Mean')
plt.axvline(x=np.median(data),
color='g', linestyle='--', label='Median')plt.axvline(x=np.mean(data) + std_dev, color='b', linestyle='--', label='1 Std Dev')plt.axvline(x=np.mean(data) - std_dev, color='b', linestyle='--')plt.axvline(x=np.mean(data) + 2*std_dev, color='black', linestyle='--', label='2 Std Dev')
plt.axvline(x=np.mean(data) - 2*std_dev, color='black', linestyle='--')plt.axvline(x=np.mean(data) + 3*std_dev, color='brown', linestyle='--', label='3 Std Dev')plt.axvline(x=np.mean(data) - 3*std_dev, color='brown', linestyle='--')plt.legend()
plt.title('正态分布数据的直方图\n方差 = {:.2f},标准差 = {:.2f}”。format(variance, std_dev))plt.xlabel('Value')
plt.ylabel('Frequency')



normal distribution
A more familiar name for the normal distribution is the bell curve, because a normal distribution forms the shape of a bell. The normal distribution is extremely important in statistics and has some specific characteristics that make it so useful.
If you take a look at the normal distribution shape presented in Figure 4.1, you may notice that the normal distribution has three fundamental characteristics. First, it is symmetrical,meaning that the higher half and the lower half of the distribution are mirror images of each other. Second, the mean, median, and mode are all in the same place, in the center of the distribution (i.e., the peak of the bell curve). Because of this second feature, the normal distribution is highest in the middle, so it is unimodal, and it curves downward toward the higher values at the right side of the distribution and toward the lower values on the left side of the distribution. Finally, the normal distribution is asymptotic, meaning that the upper and lower tails of the distribution never actually touch the baseline, also known as the X axis. This is important because it indicates that the probability of a score in a distribution occurring by chance is never zero.
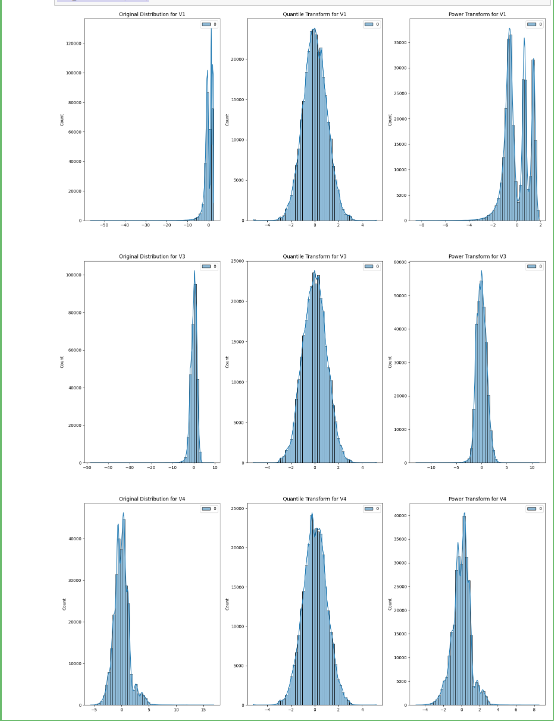
为什么偏度是一个问题?
当数据偏斜时,大多数统计模型不起作用。这背后的原因是,偏斜数据分布的锥形末端或尾部区域是数据中的异常值,我们知道异常值会严重损害统计模型的性能。最好的例子是回归模型,当训练偏斜数据时,它会显示不好的结果。
现在,正如我们所知,偏度对我们的数据不利,当数值数据具有正态分布时,许多机器学习算法更喜欢或表现更好,我们需要一种方法来消除这种偏度,为此在python中最常用的方法是PowerTransformer和QuantileTransformer。这两种方法都用于获得正态分布或类似高斯的分布。现在让我们通过一个例子看看如何使用这些方法:
df = pd.read_csv('archive/信用卡.csv')
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import pandas pd
from sklearn.preprocessing import PowerTransformer, QuantileTransformer
cols1 = [“V1”, “V3”, “V4”]
def test_transformers(columns):
pt = PowerTransformer() qt = QuantileTransformer(n_quantiles=500, output_distribution='normal') fig = plt.figure(figsize=(20,30)) j = 1 for i in columns:
array = np.array(df[i]).reshape(-1, 1)
y = pt.fit_transform(array) x = qt.fit_transform(array) plt.subplot(3,3,j) sns.histplot(array, bins = 50, kde = True,color=array) plt.title(f“Original Distribution for {i}”) plt.subplot(3,3,j+1) sns.histplot(x, bins = 50, kde = True,color=x)
plt.title(f“Quantile Transform for {i}”) plt.subplot(3,3,j+2) sns.histplot(y, bins = 50, kde = True) plt.title(f“Power Transform for {i}”) j += 3
test_transformers(cols1)