数据结构与算法--顺序存储二叉树

简介

二叉树的存储结构有两种，分别为顺序存储和链式存储

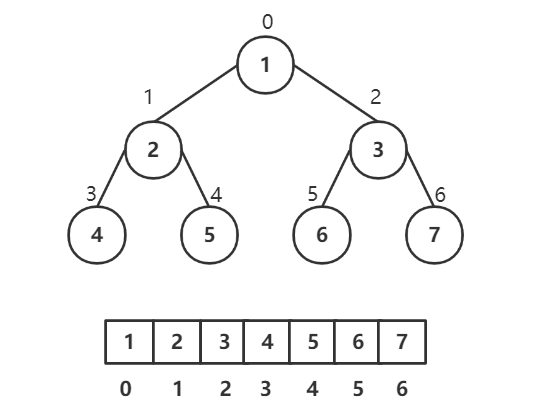
采用顺序存储。指的是使用顺序表（数组）存储二叉树。需要注意的是，顺序存储只适用于完全二叉树

• 顺序存储的完全二叉树的特征（n表示二叉树中第几个元素，按0开始编号）

  • 第n个元素的左子节点为2n+1

  • 第n个元素的右子节点为2n+2

  • 第n个元素的父节点为(n-1)/2

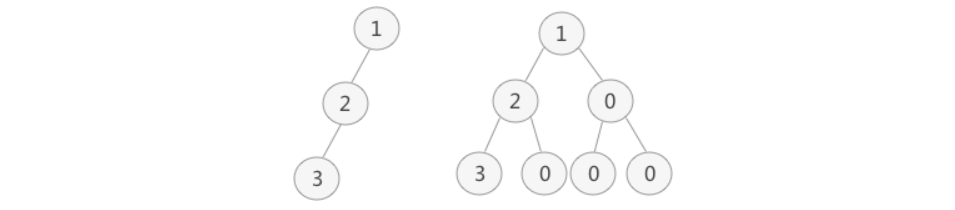
• 如果想顺序存储普通二叉树，需要提前将普通二叉树转化为完全二叉树

  • 普通二叉树转完全二叉树的方法很简单，只需给二叉树额外添加一些节点，将其"拼凑"成完全二叉树即可

    

顺序存储二叉树基础遍历

前序遍历

import java.util.LinkedList;
import java.util.Queue;

public class ArrayBinaryTree<K> {

    /**存储数据结点的数组*/
    public K[] array;

    public ArrayBinaryTree(K[] array) {
        this.array = array;
    }

    /**前序遍历*/
    public Queue<K> preErgodic(){
        Queue<K> queue = new LinkedList<>();
        if (array == null || array.length == 0) {
            return queue;
        }

        preErgodic(0,queue);
        return queue;
    }

    public void preErgodic(int index,Queue<K> queue){

        queue.add(array[index]);

        //向左，递归遍历
        if ((2 * index + 1) < array.length) {
            preErgodic(2 * index + 1,queue);
        }

        //向右，递归遍历
        if ((2 * index + 2) < array.length) {
            preErgodic(2 * index + 2,queue);
        }
    }
}

中序遍历

import java.util.LinkedList;
import java.util.Queue;

public class ArrayBinaryTree<K> {

    /**存储数据结点的数组*/
    public K[] array;

    public ArrayBinaryTree(K[] array) {
        this.array = array;
    }

    /**中序遍历*/
    public Queue<K> midErgodic(){

        Queue<K> queue = new LinkedList<>();
        if (array == null || array.length == 0) {
            return queue;
        }

        midErgodic(0,queue);
        return queue;
    }

    public void midErgodic(int index,Queue<K> queue){

        //向左，递归遍历
        if ((2 * index + 1) < array.length) {
            midErgodic(2 * index + 1,queue);
        }

        queue.add(array[index]);

        //向右，递归遍历
        if ((2 * index + 2) < array.length) {
            midErgodic(2 * index + 2,queue);
        }
    }
}

后序遍历

import java.util.LinkedList;
import java.util.Queue;

public class ArrayBinaryTree<K> {

    /**存储数据结点的数组*/
    public K[] array;

    public ArrayBinaryTree(K[] array) {
        this.array = array;
    }

    /**后续遍历*/
    public Queue<K> afterErgodic(){

        Queue<K> queue = new LinkedList<>();
        if (array == null || array.length == 0) {
            return queue;
        }

        afterErgodic(0,queue);
        return queue;
    }

    public void afterErgodic(int index,Queue<K> queue) {

        //向左，递归遍历
        if ((2 * index + 1) < array.length) {
            afterErgodic(2 * index + 1, queue);
        }

        //向右，递归遍历
        if ((2 * index + 2) < array.length) {
            afterErgodic(2 * index + 2, queue);
        }

        queue.add(array[index]);
    }
}

标签：index,--,Queue,public,queue,二叉树,array,顺序存储
来源： https://www.cnblogs.com/52-IT-y/p/16573922.html