深入浅出PID算法

前言

博主是工业互联网行码农一枚，虽然不是算法工程师和自动化方向的，但经常参加同事介绍控制算法原理的培训，慢慢的对小部分控制算法有一定了解，其中使用频率最高的控制算法非PID莫属。很多同学在学习PID的时候，会被繁杂的数学公式吓倒，今天我们就抛开数学公式，用逻辑和例子给大家讲明白“到底什么是PID”？

PID算法简介

PID是一种控制算法，是 Proportional（比例）、Integral（积分）、Differential（微分）的缩写。它是连续系统中技术最为成熟、应用最为广泛的一种控制算法。

PID控制器主要适用于基本上线性，且动态特性不随时间变化的系统。简单来说就是：类似于需要将某一个物理量“保持稳定”的场合，PID基本都能派上用场。

工业中PID典型的应用场景有：温度控制、流量控制、液位控制等。

生活中PID的应用也很常见：自来水的压力控制、空调的温度控制、平衡车的平衡控制、汽车的定速巡航控制、无人机的悬停控制、火箭飞机的姿态调整等。

实际运行经验和理论分析都表明，运用PID控制算法对许多工业过程进行控制都能得到比较满意的效果。

PID的概念及公式

PID的基本思路是根据偏差量的大小，运用比例、积分、微分计算出一个控制量，将这个控制量输入被控制的系统，系统接收到该输入量后会输出一个相应的输出量，PID控制器再检测该输出量，并再计算偏差，然后再循环以上过程。

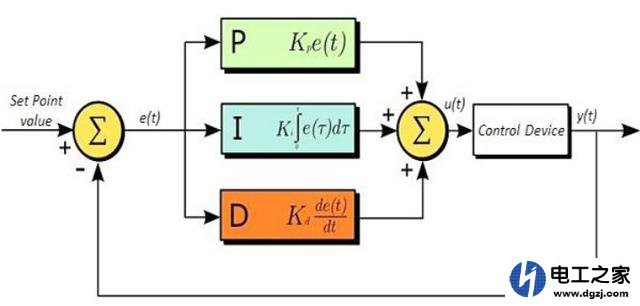
原始公式如下：
$u(t)=K_p \Bigg( e(t)+\frac{1}{T_i}\int^t_0e(t)dt+T_d\frac{de(t)}{dt}\Bigg)$

• $K_p$ —— 控制器的比例系数；
• $T_i$ —— 积分时间常数；
• $T_d$ —— 微分时间常数；
• $u(t)$ —— PID控制器的输出信号；
• $e(t)$ —— 给定值$r(t)$与测量值之差。

公式可简化为：
$u(t)=K_p * e(t) + K_i * \sum_{n=0}^t e(t) + K_d * (e(t) - e(t-1))$

• $K_p$ —— 控制器的比例系数；
• $K_i$ —— 控制器的积分系数；
• $K_d$ —— 控制器的微分系数；
• $u(t)$ —— PID控制器的输出信号；
• $e(t)$ —— 给定值$r(t)$与测量值之差。
• $e(t-1)$ —— 上一次给定值$r(t)$与测量值之差。

很多同学可能会被上面数学公式整懵了，没关系，我们先看完下面例子，再回头看来公式，相信你能对以上公式有新的认识。

在学习PID之前，我们需要先了解什么是 开环控制 和 闭环控制，这2个概念能够帮助我们更好的理解PID。

开放回路控制系统

开环控制（Open Loop Control System）：不将控制的结果反馈回来影响当前控制的系统。例如：

• 开关——按下开关后的一瞬间，控制活动已经结束，灯是否亮起已对按开关的这个活动没有影响；
• 投篮——篮球出手后就无法再继续对其控制，无论球进与否，球出手的一瞬间控制活动即结束。

闭环回路控制系统

闭环控制（Closed Loop Control System）：需要将控制的结果反馈回来与希望值比较，并根据它们的误差调整控制作用的系统。例如：

• 调节水龙头——首先在头脑中对水流有一个期望的流量，水龙头打开后由眼睛观察现有的流量大小与期望值进行比较，并不断的用手进行调节形成一个反馈闭环控制；
• 骑自行车——同理，需要不断的修正行进的方向与速度形成闭环控制。

闭环控制系统通常会由以下6个环节组成。

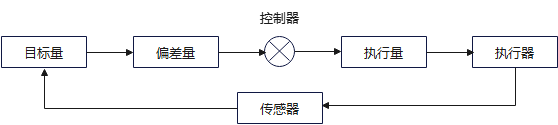
我们拿“维持水缸水位高度在1米”为例，来详解闭环控制中的每个环节：

• 传感器：人工测量当前水位高度
• 目标量：维持水缸水位高度在1米
• 偏差量：目标量 - 当前水位高度
• 控制器：根据偏差量计算出执行量
• 执行量：传给执行器的入参
• 执行器：人工用水桶向水缸中加水

其中传感器、目标量、偏差量、执行量、执行器 这5个环节都比较简单，一眼就能看明白意思。最关键的环节控制器相对复杂一些，在控制器环节选择不同的控制算法，根据偏差量计算出执行量也不同，今天我们就具体看看PID的控制效果。

PID之比例P

前面有说到PID的基本思路是根据偏差量的大小，运用比例P、积分I、微分D计算出一个控制量。但PID的3个参数，并不是非要一起使用，可以单用比例P来控制，也可以两两联合用比例P+积分I或比例P+微分D来控制。

我们先看看仅用比例P能带来什么样的控制效果？继续上面的“水缸”例子：

• 传感器：人工测量水缸初始水位高度是0.2米
• 目标量：维持水缸水位高度在1米
• 偏差量：1米 - 0.2米 = 0.8米
• 控制器：使用PID算法的比例控制，根据偏差量计算出执行量
• 执行量：传给执行器的入参
• 执行器：人工用水桶向水缸中加水

通常情况偏差量和执行量之间的单位不同，在当前例子里偏差量的单位是水缸，而执行量的单位是水桶，他们的容积不一样，所以我们需要一个系数，来放大或者缩小两者的关系。具体公式可抽象为：

执行量 = 比例P = 偏差量 * 比例P系数

这个时候，假设水缸旁边站着一个人，用水桶往水缸里加水来控制水位的高度。如果单纯的用比例控制算法，假设比例P系数是0.5（相当于两桶水的容量等于一缸水的容量），我们开始模拟加水实验：

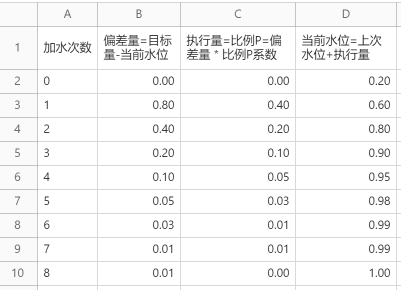
如上图结果所示，人工用水桶向水缸中加水8次，就能把水缸水位加到1米高度。把当前水位转换成曲线，大概效果如下。

上述例子比较简单，单靠比例P就能完成任务，但现实情况往往只有比例P是不够的，我们再来看一个更复杂的情况，假设比例P系数仍然是0.5，但在每次加水的间隔，水缸都会漏掉0.1米高度的水。我们再从头模拟加水实验，看看具体结果会怎样？

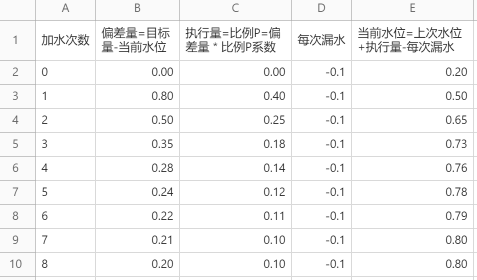
如上图结果所示，当水位达到0.8之后，水位就不会继续增加了。因为，当水位等于0.8时，偏差量是0.2，每次往水缸中加水的量为执行量= 比例P= 0.2 * 0.5 = 0.1，而每次加水的间隔，水缸都会漏掉0.1米高度的水，所以加入的水和流出的水相抵消。

虽然，此时控制系统已达稳定状态，但实际值与目标量之间的会存在一个稳定差值，这个差值叫稳态误差。稳态误差非常常见，比如：控制空调温度会因为空气温差而降温、控制无人机固定高度会受重力影响往下掉、控制汽车定速巡航会有空气阻力和摩擦力的影响而减速，这些场景都会产生稳态误差。

单单只用比例P控制闭环回路，是无法避免稳态误差问题的，因为比例P系数无法根据时间或次数累加，当存在外界干扰因素时，比例P系数无法动态调整大小，那么稳态误差就会一直存在。

假如我们引入时间的维度，就能获得2个神器 增幅器-积分I 和 抑制器-微分D，他们分别解决比例P过小和过大的情况，比例P过小的话由增幅器-积分I 补充即可解决稳态误差问题，比例P过大由抑制器-微分D消减来防止过度震荡。

PID之积分I（增幅器）

我们先来看看增幅器积分I，它也可以理解为累加经验，当比例P过小，可以由积分I补充，它的原理是利用过去的时间不断累加。具体公式可抽象为：

比例P = 偏差量 * 比例P系数
积分I = 上一次积分I + 偏差量 * 积分I系数
执行量 = 比例P + 积分I

想象一下，如果用只比例P控制存在稳态误差，说明比例P过小，这时积分I就会不断累加到一个很大的值，来补充比例P，从而影响执行量。

如果最终控制效果在目标量附近抖动，我们就能得到一个正负交替的偏差量，会在目标附近不断产生正负数累加到积分I，积分I就会不断趋近于零，最终使控制效果趋于稳定。

我们继续用上面“水缸加水”的例子，假设目标量是1，每次漏水0.1，比例P系数为0.5，积分I系数为0.2，我们再从头模拟加水实验，具体数值如下。

把当前水位转换成曲线，大概效果如下。

上一轮实验只用比例P控制存在稳态误差。本轮实验加入了积分I之后就有了累加效果，在未达到控制效果之前积分I会持续累加，在达到目标量之后积分I因为惯性会继续过量控制 ，同时偏差量会由正转负再转正，积分I也会由正转负再转正，最终积分I会持续抵消掉每次漏水0.1，控制效果趋于稳定 。

增幅器有他的危险性，如果系统出现意外或错误，增幅器可能会被累加到无限大，导致系统不可用，所以增幅器需要有一定的限制。

• 1、限制幅度，在任意时刻都给积分I设定最大值和最小值。
• 2、不运行时清零，当系统判断没有运行时，主动将积分I清零。

PID之微分D（抑制器）

我继续再看看抑制器微分D，它也可以理解为预测未来，用当前的偏差量减上一次偏差量，得到的结果就可能是下一次偏差量，用下一次偏差量提前参与到计算中，就可以防止执行量过大，产生超出目标量的问题。具体公式可抽象为：

比例P = 偏差量 * 比例P系数
积分I = 上一次积分I + 偏差量 * 积分I系数
微分D = (偏差量 - 上一次偏差量) * 微分D系数
执行量 = 比例P + 积分I + 微分D

换个“汽车刹车”的例子，平稳驾驶的车辆，当发现前面有红灯时，为了使得行车平稳，基本上提前几十米就松油门踩刹车。当车辆离停车线非常近的时候，则使劲踩刹车使车辆停下来，整个过程可以看做一个加入微分D的控制策略。

可以看到，在刹车过程中，因为偏差量是越来越小的，所以 微分D= (偏差量-上一次偏差量)*微分D系数一定是负数，在控制中加入一个负数项，他存在的作用就是为了防止汽车由于刹车不及时而闯过停车线。

从常识上理解，越靠近停车线，就越应该踩深刹车，不能让车过线，所以这个 微分D的作用，可以理解为刹车。当车离停车线很近，并且车速还很快时，这个 微分D的绝对值（实际上是一个负数）就会很大，表示应该大力踩刹车尽快让车停下来。

再回到上面“水缸加水”的例子，当发现水缸里的水快要接近目标量时，加入 微分D可以减少过量加水的幅度，说白了就是减少控制过程中的震荡。假设目标量是1，每次漏水0.1，比例P系数为0.5，积分I系数为0.2，微分D系数为0.2，我们再从头模拟加水实验，具体数值如下。

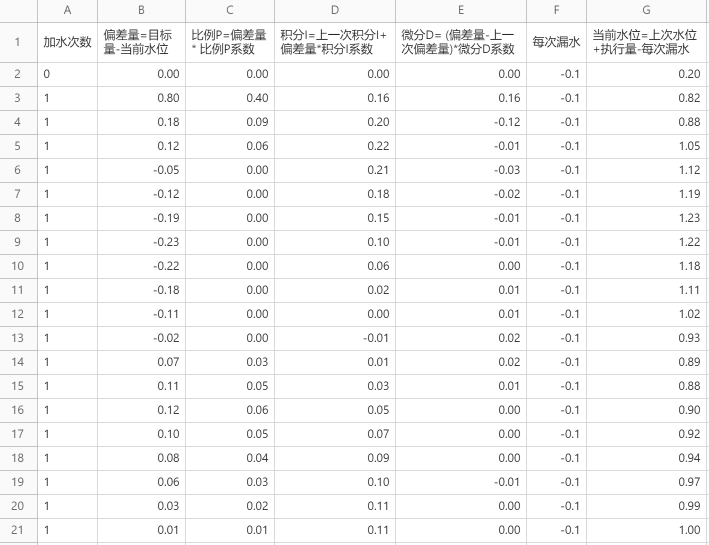
上一轮实验使用比例P和积分I联合控制，最高水位达到1.3，超过目标量之后，水位最低回落至0.83。本轮实验加入了抑制器微分D之后，最高水位仅达到1.23，超过目标量之后，水位最低回落至0.88，相比上一轮实验，本轮震荡幅度明显减小，这就是微分D的抑制作用。

分享一个动图，很好的展示了比例P、积分I、微分D的控制效果，其中红色虚线是目标量，曲线是用当前值的变化趋势。结合这个动图，大家再回想一下“水缸加水”的例子，控制效果是不是很相似呀~

PID原理总结

我们用了“水缸加水”的例子，详细解释了PID的比例P、积分I、微分D三个参数的控制原理，相信小伙伴们已经明白什么是PID了。大家再回过头看这个公式，是不是也觉得挺亲切的。
$u(t)=K_p * e(t) + K_i * \sum_{n=0}^t e(t) + K_d * (e(t) - e(t-1))$

• $K_p$ —— 控制器的比例系数；
• $K_i$ —— 控制器的积分系数；
• $K_d$ —— 控制器的微分系数；
• $u(t)$ —— PID控制器的输出信号；
• $e(t)$ —— 给定值$r(t)$与测量值之差（偏差量）；
• $e(t-1)$ —— 上一次给定值$r(t)$与测量值之差。

最后再总结一下：

• 比例P、积分I、微分D都跟偏差量有关
• 比例P取决于当前的偏差量
• 积分I累计过去所有偏差量之和
• 微分D预测下一时刻偏差量

所以，经常有人说比例P是现在，积分I是过去，微分D是未来，是不是有一种哲学的感觉，哈哈~

PID调参口诀

最后分享个PID调参口诀，写得挺好还挺押韵的~

参数整定找最佳，从小到大顺序查；
先是比例后积分，最后再把微分加；
曲线振荡很频繁，比例度盘要放大；
曲线漂浮绕大湾，比例度盘往小扳；
曲线偏离回复慢，积分时间往下降；
曲线波动周期长，积分时间再加长；
曲线振荡频率快，先把微分降下来；
动差大来波动慢。微分时间应加长；
理想曲线两个波，前高后低4比1；
一看二调多分析，调节质量不会低；
若要反应增快，增大P减小I;
若要反应减慢，减小P增大I；
如果比例太大，会引起系统振荡；
如果积分太大，会引起系统迟钝。

参考引用

• 百度百科-PID算法
• 百度百科-开环控制
• PID控制入门原理：https://zhuanlan.zhihu.com/p/197927959
• PID控制算法原理：https://zhuanlan.zhihu.com/p/39573490
• PID控制原理及控制框图说明：https://www.dgzj.com/zidonghua/96044.html
• PID参数调整，个人经验：https://blog.csdn.net/weixin_44407238/article/details/119255699
• 学会PID-基于板球平衡系统：https://www.bilibili.com/video/BV1xL4y147ea

如有任何问题或建议，欢迎前往公众号【劼哥舍】留言~

标签：偏差,控制,积分,深入浅出,PID,微分,算法,比例
来源： https://www.cnblogs.com/shi0090/p/16251924.html