LeetCode力扣84.柱状图中最大的矩形

题目描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。

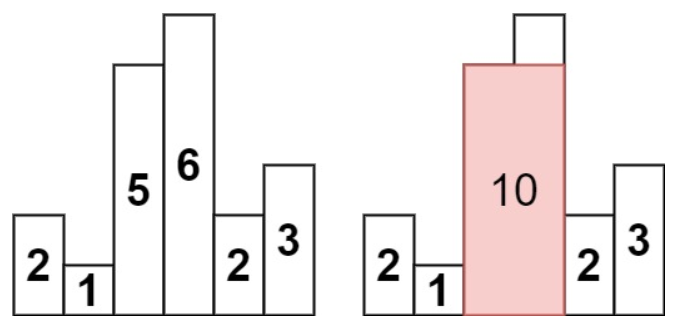
输入输出样例

输入 #1

6
2 1 5 6 2 3

输出 #1

10

解释：最大的矩形为图中红色区域，面积为 10

解题思路

首先第一眼可以看出本题用暴力法一定可以做出来，但纯暴力一般会超时，可以借助单调栈对暴力法进行优化。

先说暴力法，最外层循环遍历 n 根柱子，内部对每根柱子左右分别进行 while 循环找到第一根高度小于当前高度的柱子，就可以算出以当前柱子为高时矩形的最大面积，遍历结束即可找出矩形最大面积。

单调栈法，依旧是最外层循环遍历 n 根柱子，并且只在栈中存储高度递增的柱子的数组下标。比如第 i 根柱子的高度大于栈顶的柱子高度时，就让i入栈，小于栈顶柱子高度，说明以栈顶为高的矩形找到了右边界，而栈中存储的是递增的序列，那么左边界也确定了，左右边界做差就得到了矩形的宽，那么以栈顶为高的矩形的最大面积就确定了，将面积与之前记录的最大面积进行比较，更新最大面积。遍历结束就得到了最终结果。这样就省去了纯暴力中每次循环查找左右边界的过程。光看文字看不懂，这里建议看代码画图自己模拟一遍。

要注意的是最外层遍历要多执行一次,for(int i=0;i<=n;i++)，下标为 n 的数组中存柱子高度为0，因为如果出现 n 根柱子高度恰好为递增序列的情况，那么程序不会对最大面积进行更新。

代码

此代码不支持上机检测。

#include<iostream>
#include<algorithm>
#include<stack>

using namespace std;

int n;	//柱子数量 
int max_area;	//记录当前最大面积 
int area;	//记录以当前柱子为高的最大面积 
int height[100005];	//存储柱子高度 
stack<int> s;	//存储高度递增的柱子的数组下标 

int main()
{
	cin>>n;
	for(int i=0;i<n;i++)
		cin>>height[i];
	for(int i=0;i<=n;i++)
	{
		while(!s.empty()&&height[s.top()]>height[i])	//栈非空且第i根柱子高度栈顶柱子高度，此时不能入栈，开始计算面积 
		{
			if(s.size()==1) area=height[s.top()];	//当栈中仅有一个元素，矩形高为柱子高度宽为1 
			else area=height[s.top()]*(i-s.top());	//当栈中有多个元素，矩形高为栈顶柱子高度，宽为左右第一个比当前柱子矮的两柱子的间距即i-s.top 
			max_area=max(max_area,area);	//与之前记录的最大面积作比较，更新最大面积 
			s.pop();	//已做过高的柱子出栈 
		}
		s.push(i);	//栈空或者栈顶柱子高度小于第i根柱子高度，下标入栈 
	}
	cout<<max_area;
	return 0;
}

标签：柱子,area,int,面积,高度,C++,力扣,柱状图,矩形
来源： https://www.cnblogs.com/LoginX/p/Login_X3.html