UVA - 1393 Highways （和紫书不一样的解法）

题目链接

题解：

由于我的方法和紫书不一样，所以专门写一下记录一下解题思路。

显然“\”和“/”两个方向的直线数量是相同的，所以我们考虑计算“/”方向的线的数量。

统计类问题，都需要找到合适的分类方法，使我们能够不重复、不遗漏的统计出所有情况。

本题我们以直线的起点分类，把直线分类，来进行统计。

对于点，其右上角有个点，总共可以连条直线，其中某些直线重复出现，假如我们计算出只出现了一次的直线有多少条记为。那么所有点的的和，即，就是我们的答案。

很容易证明，对于每条直线，我们只会在最右上角那一段计算一次，所以不会有重复，我们计算了所有起点，所以没有遗漏。

对于每一个点，如何计算 ？

我们设点为坐标源点，设其右上角的点坐标为。

我们要直线只出现一次，那么一定要同时满足以下条件：

1，

2， 或 

如何计算满足条件的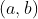有多少对呢？

我们设为有多少对互质？即

那么 就是要求解的答案。

如何计算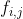呢？

我们可以递推计算 ，表示数字1到有多少个数和互素。

我们可以暴力预处理出所有

复杂度

预处理的复杂度

每次询问计算的复杂度

所以复杂度为

代码如下：

#include<bits/stdc++.h>

using namespace std;
const int nn =11000000;
const int inff = 0x3fffffff;
const double eps = 1e-8;
typedef long long LL;
const double pi = acos(-1.0);
const LL mod = 1000000007;
int f[310][310];
int GCD(int a,int b)
{
    if(b==0)
        return a;
    return GCD(b,a%b);
}
void init()
{
    memset(f,0,sizeof(f));
    int pre[310];
    memset(pre,0,sizeof(pre));
    for(int i=1;i<=300;i++)
    {
        f[i][1]=f[i-1][1]+1;
        for(int j=1;j<=300;j++)
        {
            if(GCD(i,j)==1)
                pre[j]++;
        }
        for(int j=2;j<=300;j++)
        {
            f[i][j]=f[i][j-1]+pre[j];
        }
    }
}
int main()
{
    init();
    int n,m;
    while(cin>>n>>m)
    {
        if(n==0&&m==0)
            break;
        LL ans=0;
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                ans+=f[i-1][j-1]-f[(i-1)/2][(j-1)/2];
            }
        }
        cout<<ans*2<<endl;
    }
    return 0;
}

标签：直线,const,紫书,latex,int,复杂度,Highways,计算,UVA
来源： https://blog.csdn.net/madaidao/article/details/115527717