树1

 

树结构

 

树是一种数据结构，它由结点以及连接结点的边构成。

如果一棵树具有名为“根”的特殊结点，那么这棵树称作有根树。

结点之间具有父子关系，结点上方的那个结点称为该结点的父结点，下方与该结点连接的结点称为该结点的子结点，结点的子结点数称为该结点的度。

没有子结点的结点称为外部结点或叶结点，除叶结点以外的结点称为内部结点。

从跟到结点x的路劲长度称为x的深度，结点x到叶结点的最大路劲长度称为结点x的高，根结点的高度称为树高。

 

二叉树

 

如果一棵树拥有一个根结点，且所有结点的子结点数都不超过2，那么这棵树称为有根二叉树。

 

有序树

 

将子结点有特定顺序的二叉树称为有序树。

如下图： 

 

有根树的表达例题

编写一个程序，输出给定的有根树中各结点的信息：

• u的结点编号。

• u的结点种类。

• u的父结点编号。

• u的子结点列表。

• u的深度。

输入：

第一行输入n。

之后每个结点信息占一行。

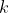
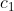
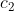
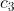
     id为结点编号，k为度，之后为子结点编号。

输出：

每个结点的父结点，深度，结点类型以及子结点列表。

 

在存储有根树时，可以运用“左子右兄弟表示法”：

• 结点u的父结点

• 结点u的最左侧结点

• 结点u右侧紧邻的兄弟结点

 

左子右兄弟表示法的实现：

struct node { int p, l, r; };

 node t[max];

如果u.p不存在，说明结点u为根，如果u.l不存在，说明结点u是叶结点，如果u.r不存在，说明结点u为最右侧结点。

 

求结点的深度：

int getdepth(u) {
	d = 0;
	while (t[u].p != nil) {
		t[u] = t[u].p;
		d++;
	}
	return d;
}

 

用下面的方法可以更快求出结点的深度（递归）：

void getdepth(u,p) {
	d[u] = p;
	if (t[u].r != nil)getdepth(t[u].r, p);
	if (t[u].l != nil)getdepth(t[u].l, p + 1);
}

 

完整代码如下：

#include<iostream>
using namespace std;
#define max 10000
#define nil -1

struct node { int p, l, r; };
node t[max];
int n, d[max];

void getdepth(int u,int p) {
	d[u] = p;
	if (t[u].r != nil)getdepth(t[u].r, p);
	if (t[u].l != nil)getdepth(t[u].l, p + 1);
}

void print(int u) {
	int i,c;
	cout << "node" << u << ":";
	cout << "p=" << t[u].p << ",";
	cout << "depth=" << d[u] << ",";

	if (t[u].p == nil)cout << "root";
	else if (t[u].l == nil)cout << "leaf";
	else cout << "internal node";

	cout << "[";

	for (i = 0,c=t[u].l;c!=nil; i++,c=t[c].r) {
		cout << c<<" ";
	}
	
	cout <<"]"<< endl;
}
int main() {
	
	int i,v, d, l, c,cur=0;

	cin >> n;
	
	for (int i = 0; i < n; i++) {
		t[i].p = t[i].l = t[i].r = nil;
	}

	for (int i = 0; i < n; i++) {
		cin >> v >> d;
		for (int i = 0; i < d; i++) {
			cin >> c;
			if (i == 0)t[v].l = c;
			else t[l].r = c;
			l = c;
			t[c].p = v;
		}
	}

	for (int i = 0; i < n; i++){
		if(t[i].p==nil)cur=i;
	}

	getdepth(cur,0);
	
	for (i = 0; i < n; i++) {
		print(i);
	}

}

 

如果树高为h，那么求所有结点的深度时，算法复杂度为O（nh）。

如果用递归求结点深度，只需遍历每个结点，所以算法复杂度为O（n）；

---

读《挑战程序设计竞赛》第十九天（侵删）2021.3.15

标签：结点,getdepth,nil,树结构,int,++,称为
来源： https://blog.csdn.net/weixin_51302676/article/details/114832389