图像处理技术运用(1)-空域图像增强之图像基本运算和灰度变换、直方图技术
作者：互联网
引言：
本文简要介绍了空域图像增强中的图像基本运算和灰度变换、直方图技术。MATLAB函数具体使用可以查看MATLAB官方文档。
https://ww2.mathworks.cn/help/
1.1 图像相加运算
- 原理表达式
Z ( x , y ) = a 1 X 1 ( x , y ) + a 2 X 2 ( x , y ) + ⋯ a n X n ( x , y ) + c Z(x,y)=a_1X_1(x,y)+a_2X_2(x,y)+\cdots a_nX_n(x,y)+c Z(x,y)=a1X1(x,y)+a2X2(x,y)+⋯anXn(x,y)+c
其中 Z ( x , y ) Z(x,y) Z(x,y)为结果图像， X n ( x , y ) X_n(x,y) Xn(x,y)为加法运算的图像， a n a_n an为进行图像相加运算图像各自的权重， c c c是一常数。
- 运用场景
（1）把同一景物的多重影像相加求平均，可降低图像中的随机噪声。
（2）在图像上叠加上指示框、说明文字等信息。
（3）对图像进行特定的补偿，如增强总体亮度等。
- MATLAB相关函数
imadd imlincomb
1.2 图像相减运算
- 原理表达式
Z ( x , y ) = X 1 ( x , y ) − X 2 ( x , y ) Z(x,y)=X_1(x,y)-X_2(x,y) Z(x,y)=X1(x,y)−X2(x,y)
其中 Z ( x , y ) Z(x,y) Z(x,y)为结果图像， X 1 ( x , y ) X_1(x,y) X1(x,y)和 X 2 ( x , y ) X_2(x,y) X2(x,y)为减法运算的图像。很多时候上式会取绝对值，以得到非负的图像像素值。
Z ( x , y ) = ∣ X 1 ( x , y ) − X 2 ( x , y ) ∣ Z(x,y)=|X_1(x,y)-X_2(x,y)| Z(x,y)=∣X1(x,y)−X2(x,y)∣
- 运用场景
（1）在背景比较容易获得时，直接减除图像背景。
（2）对同一景物在不同时间拍摄的图像或同一景物在不同时间的图像进行减法运算，可用来减去背景，如在刑事中提取指纹，在实时运动中进行运动检测等。
（3）将处理前后的两幅图像进行比对，找出处理效果。
（4）进行梯度运算，通过灰度值变化大的地方找到物体的边界。
- MATLAB相关函数
imsubstract imabsdiff
1.3 图像相乘运算
- 原理表达式
Z ( x , y ) = X 1 ( x , y ) × X 2 ( x , y ) Z(x,y)=X_1(x,y)\times X_2(x,y) Z(x,y)=X1(x,y)×X2(x,y)
其中 Z ( x , y ) Z(x,y) Z(x,y)为结果图像， X 1 ( x , y ) X_1(x,y) X1(x,y)和 X 2 ( x , y ) X_2(x,y) X2(x,y)为乘法运算的输入图像。
- 运用场景
（1）求一幅图像各像素点的平方值，使图像高亮度区对比度进一步增强，低亮度区对比度进一步减弱。
（2）对图像亮度进行补偿
（3）图像掩膜处理
- MATLAB相关函数
immultiply
1.4 图像相除运算
- 原理表达式
Z ( x , y ) = X 1 ( x , y ) / X 2 ( x , y ) Z(x,y)=X_1(x,y)/ X_2(x,y) Z(x,y)=X1(x,y)/X2(x,y)
其中 Z ( x , y ) Z(x,y) Z(x,y)为结果图像， X 1 ( x , y ) X_1(x,y) X1(x,y)和 X 2 ( x , y ) X_2(x,y) X2(x,y)为除法运算的输入图像。
- 运用场景
（1）对图像进行归一化处理。
- MATLAB相关函数
imdivide
1.5 图像取补运算
- 原理表达式
Z ( x , y ) = X ( x , y ) ‾ Z(x,y)=\overline {X(x,y)} Z(x,y)=X(x,y)
其中 Z ( x , y ) Z(x,y) Z(x,y)为结果图像， X ( x , y ) X(x,y) X(x,y)为取补前原始图像。
- 运用场景
（1）将目标与背景调换，即将原先的目标变为背景，将原先的背景变为目标。
（2）对相片底片图像进行取补操作可得到真实景象。
- MATLAB相关函数
imcomplement
1.6 图像逻辑运算
- 原理表达式
Z ( x , y ) = X ( x , y ) a n d Y ( x , y ) Z(x,y)=X(x,y)\quad and \quad Y(x,y) Z(x,y)=X(x,y)andY(x,y)
Z ( x , y ) = X ( x , y ) o r Y ( x , y ) Z(x,y)=X(x,y)\quad or \quad Y(x,y) Z(x,y)=X(x,y)orY(x,y)
Z ( x , y ) = n o t X ( x , y ) Z(x,y)=not\quad X(x,y) Z(x,y)=notX(x,y)
Z ( x , y ) = X ( x , y ) x o r Y ( x , y ) Z(x,y)=X(x,y)\quad xor \quad Y(x,y) Z(x,y)=X(x,y)xorY(x,y)
Z ( x , y ) = X ( x , y ) = = Y ( x , y ) Z(x,y)=X(x,y)\quad == \quad Y(x,y) Z(x,y)=X(x,y)==Y(x,y)
- 运用场景
（1）针对二值图像，在图像形态学处理、图像分割和图像分析等领域有广泛应用。
- MATLAB相关函数
and or not xor ==
1.7 图像灰度变换
- 原理表达式
（1）灰度线性变换
g
′
(
x
,
y
)
=
{
c
0
≤
g
(
x
,
y
)
<
a
d
−
c
b
−
a
[
g
(
x
,
y
)
−
a
]
+
c
a
≤
g
(
x
,
y
)
<
b
d
b
≤
g
(
x
,
y
)
<
255
g'(x,y)=\left\{\begin{matrix} c \quad\quad\quad\quad\quad\quad\quad\quad\quad0\le g(x,y)<a\\ \frac{d-c}{b-a}[g(x,y)-a]+c \quad a\le g(x,y)<b \\ d\quad\quad\quad\quad\quad\quad\quad\quad b\le g(x,y)<255\\ \end{matrix}\right.
g′(x,y)=⎩⎨⎧c0≤g(x,y)<ab−ad−c[g(x,y)−a]+ca≤g(x,y)<bdb≤g(x,y)<255
灰度线性变换是将图像中某一区域的灰度值通过线性拉伸至一个更大的范围，使原本位于该区域的图像对比度得到增强。把原图像 g ( x , y ) g(x,y) g(x,y)从 [ a , b ] [a,b] [a,b]的范围拉伸至 [ c , d ] [c,d] [c,d], [ a , b ] [a,b] [a,b]不一定是图像 g ( x , y ) g(x,y) g(x,y)的最小值和最大值，它可以是任意用户感兴趣的灰度区域，只要范围 [ c , d ] [c,d] [c,d]比 [ a , b ] [a,b] [a,b]大，就可以起到增强对比度的效果，其函数图形如左图所示。
（2）分段线性变换
g ′ ( x , y ) = { c a g ( x , y ) 0 ≤ g ( x , y ) < a d − c b − a [ g ( x , y ) − a ] + c a ≤ g ( x , y ) < b 255 − d 255 − b [ g ( x , y ) − b ] + d b ≤ g ( x , y ) ≤ 255 g'(x,y)=\left\{\begin{matrix} \frac{c}{a}g(x,y) \quad\quad\quad\quad\quad\quad\quad0\le g(x,y)<a\\ \frac{d-c}{b-a}[g(x,y)-a]+c \quad\quad a\le g(x,y)<b \\ \frac{255-d}{255-b}[g(x,y)-b]+d\quad\quad b\le g(x,y)\le 255\\ \end{matrix}\right. g′(x,y)=⎩⎨⎧acg(x,y)0≤g(x,y)<ab−ad−c[g(x,y)−a]+ca≤g(x,y)<b255−b255−d[g(x,y)−b]+db≤g(x,y)≤255
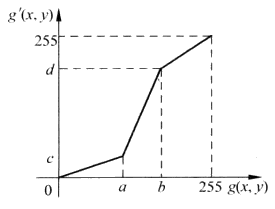
分段灰度变换是将图像的灰度分割为若干个区间，对这些区间分别进行线性变换的操作。分段线性变换更加灵活，可以拥有多个用户感兴趣的灰度区域，对线性变换稍作修改，就可以得到一个分段线性变换函数，左图将图像 g ( x , y ) g(x,y) g(x,y)的灰度分割为三段： [ 0 , a ) , [ a , b ) , [ b , 255 ] [0,a),[a,b),[b,255] [0,a),[a,b),[b,255]。
（3）非线性变换
非线性灰度变换对应于非线性映射函数，典型的映射包括平方函数、对数函数、指数函数、截取函数、阈值函数和多值量化函数等。
左图是指数映射关系曲线的形状，如果gamma小于1，则映射曲线为上凸曲线，如左图图（a）所示，如果gamma大于1，则映射曲线为下凸曲线，如左图图（b）所示，一般gamma默认为1表示线性映射，如左图（c）所示，当gamma等于2时，该函数等价于平方函数。
- 运用场景
提高对比度，使得图像的灰度层次更加清晰可辨。
- MATLAB相关函数
imadjust
1.8 图像直方图技术
- 原理表达式
p r ( r k ) = n k n k = 0 , 1 , 2 , ⋯ , L − 1 p_r(r_k)=\frac{n_k}{n}\quad k=0,1,2,\cdots,L-1 pr(rk)=nnkk=0,1,2,⋯,L−1
式中， n n n为一幅图像的总像素， n k n_k nk为第 k k k级灰度的像素数， r k r_k rk表示第 k k k个灰度等级， p r ( r k ) p_r(r_k) pr(rk)表示该灰度出现的相对概率，这 L L L个概率值 p r ( r k ) p_r(r_k) pr(rk)组成的一维向量 h i s t [ 0 , ⋯ , L − 1 ] hist[0,\cdots,L-1] hist[0,⋯,L−1]即为图像的直方图。
若图像具有 L L L（通常 L L L=256，即8位灰度级）级灰度，则大小为 M × N M\times N M×N的灰度图像 g ( x , y ) g(x,y) g(x,y)的灰度直方图 h i s t [ 0 , ⋯ , L − 1 ] hist[0,\cdots,L-1] hist[0,⋯,L−1]可用如下计算获得。
①初始化 h i s t [ k ] = 0 ; k = 0 , ⋯ , L − 1 hist[k]=0;k=0,\cdots,L-1 hist[k]=0;k=0,⋯,L−1
②统计 h i s t [ g ( x , y ) ] + + ; x , y = 0 , ⋯ , M − 1 , 0 , ⋯ , N − 1 hist[g(x,y)]++;x,y=0,\cdots,M-1,0,\cdots,N-1 hist[g(x,y)]++;x,y=0,⋯,M−1,0,⋯,N−1
③标准化 h i s t [ g ( x , y ) ] / = ( M × N ) hist[g(x,y)]/=(M\times N) hist[g(x,y)]/=(M×N)
（1）直方图均衡的原理
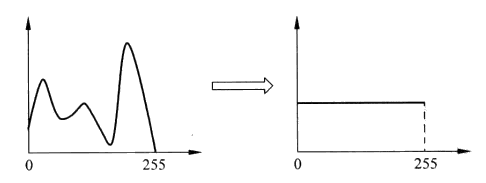直方图均衡操作是对图像直方图进行处理，使得处理后的图像直方图为平坦形状。直方图均衡需要完成的任务可以用到左图来说明。
实现直方图变换可以用到如下灰度变换公式。
s = f ( r ) = ∫ 0 r p r ( w ) d w s=f(r)=\int_0^rp_r(w)dw s=f(r)=∫0rpr(w)dw
式中 r r r代表待增强图像的某个灰度值， p r ( w ) p_r(w) pr(w)为变量 r r r的概率密度函数， f f f为亮度变换函数， s s s为亮度变换后新的灰度值。
不过一般是离散情况，因为图像的灰度值是由精度限制的，且图像的像素数目是有限的，这就导致变量r或s是一个离散的随机变量，对由 L L L种灰度值取值可能的离散随机白能量 r r r来说，原图像灰度值 r k r_k rk出现的概率近似为：
p r ( r k ) = n k n k = 0 , 1 , 2 , ⋯ , L − 1 p_r(r_k)=\frac{n_k}{n}\quad k=0,1,2,\cdots,L-1 pr(rk)=nnkk=0,1,2,⋯,L−1
s k = T ( r k ) = Σ j = 0 k p r ( r j ) = Σ j = 0 k n j n k = 0 , 1 , 2 , ⋯ , L − 1 s_k=T(r_k)=\Sigma_{j=0}^kp_r(r_j)=\Sigma_{j=0}^k\frac{n_j}{n}\quad k=0,1,2,\cdots,L-1 sk=T(rk)=Σj=0kpr(rj)=Σj=0knnjk=0,1,2,⋯,L−1
- 运用场景
让图像的灰度值跨越更大的范围。
- MATLAB相关函数
histeq
参考资料
[1]高展宏，徐文波.《MATLAB的图像处理案例教程》[M].北京：清华大学出版社 83-106
标签：函数,灰度变换,直方图,灰度,MATLAB,图像,quad,图像增强 来源： https://blog.csdn.net/subtitle_/article/details/114548483