股票最大收益_1

leetcode 剑指offer63

degree:mid

description:

假设把某股票的价格按照时间先后顺序存储在数组中，请问买卖该股票一次可能获得的最大利润是多少？

examples

示例 1:

输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。

示例 2:

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

 

限制：

0 <= 数组长度 <= 10^5

自己的解题过程：

想要把数组升序排序，建立值和原始序号的map；然后运用两个循环，外循环从第一个元素开始递增到最后一个，内循环从最后一个递减到当前最小，然后内循环当前最大的和外循环当前最小的，如果他们的index不“冲突”，则可以实现

设共有 nnn 天，第 aaa 天买，第 bbb 天卖，则需保证 a<ba < ba<b ；可推出交易方案数共有：

\((n−1)+(n−2)+⋯+2+1=n(n−1)/2(n - 1) + (n - 2) + \cdots + 2 + 1 = n(n - 1) / 2 (n−1)+(n−2)+⋯+2+1=n(n−1)/2\)

自己的这种想法的时间复杂度还是 o(n*2) ，甚至暴力法还没有写的很简单：

解决方案

我们需要找出给定数组中两个数字之间的最大差值（即，最大利润）。此外，第二个数字（卖出价格）必须大于第一个数字（买入价格）。

形式上，对于每组 i 和 j（其中 j>i）我们需要找出

\[max⁡(prices[j]−prices[i]) \]

然后官方的暴力法:

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = (int)prices.size(), ans = 0;
        for (int i = 0; i < n; ++i){
            for (int j = i + 1; j < n; ++j) {
                ans = max(ans, prices[j] - prices[i]);
            }
        }
        return ans;
    }
};

实际上，这点可以看出自己饶了很大的圈子，虽然最后程序调试成功了，但是从复杂度上来说是很差的程序。一开始自己想到了动态规划，但是由于一开始的出发点就是从程序能不能运行的角度去思考的，没有把条件判断总结出来，实际上这道题可以从很通俗的角度思考，但是本质还是动态规划dp。经过参考大佬的思路后，下面从两个角度分析这道题：

[1]

算法：

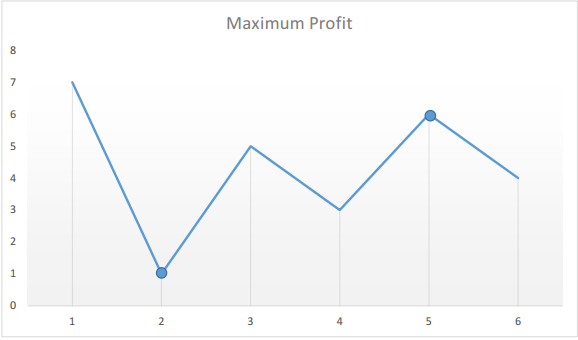
假设给定的数组为：[7, 1, 5, 3, 6, 4]

如果我们在图表上绘制给定数组中的数字，我们将会得到：

我们来假设自己来购买股票。随着时间的推移，每天我们都可以选择出售股票与否。那么，假设在第 i 天，如果我们要在今天卖股票，那么我们能赚多少钱呢？

显然，如果我们真的在买卖股票，我们肯定会想：如果我是在历史最低点买的股票就好了！太好了，在题目中，我们只要用一个变量记录一个历史最低价格 minprice，我们就可以假设自己的股票是在那天买的。那么我们在第 i 天卖出股票能得到的利润就是 prices[i] - minprice。

因此，我们只需要遍历价格数组一遍，记录历史最低点，然后在每一天考虑这么一个问题：如果我是在历史最低点买进的，那么我今天卖出能赚多少钱？当考虑完所有天数之时，我们就得到了最好的答案。

• code与下面动态规划的code一致

这里和自己想法的不同是：

不是去寻找所有天数中最低价格，(我这里想法的原因就是开头的那种想法，实际上：

我感觉算法到目前为止，很多抽象的，共性的大方向上的思考方法都已经被总结出来了，如果从时间复杂度上，自己要从更优的思考方法上着手，因为那些低时间复杂度的方法都是一种形而上的思想，是为了特定的条件而被思考和总结出来的，以后要多学习！

• 去把“那本算法书“给看了！！！！！！！

)，而是考虑前 \(i\) 天的最低价格，这也是为什么前面说这道题的思路实际上是 DP 的原因

下面解释如何从动态规划的角度考虑：

[2]

​

动态规划解析：

• 状态定义： 设动态规划列表 dp ，dp[i]代表以 prices[i]为结尾的子数组的最大利润（以下简称为 前 iii 日的最大利润 ）。

• 转移方程： 由于题目限定 “买卖该股票一次” ，因此前 i 日最大利润 dp[i] 等于前 i−1最大利润 dp[i−1]和第 i 日卖出的最大利润中的最大值。

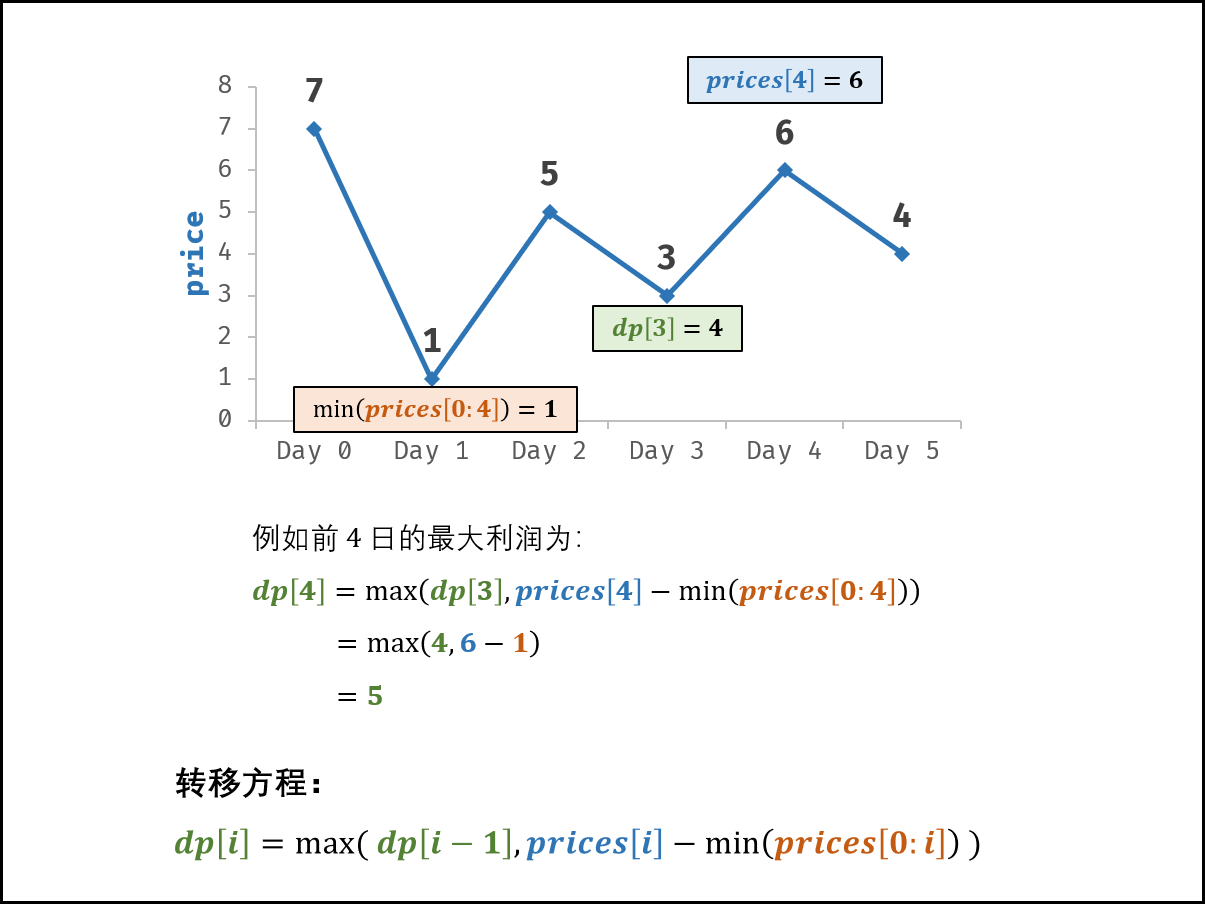
前i日最大利润=max⁡(前(i−1)日最大利润,第i日价格−前i日最低价格)

\(dp[i]=max⁡(dp[i−1],prices[i]−min⁡(prices[0:i]))\)

(这个dp方程不仅考虑了前一天的，还有前 \(i\) 天的信息！！)

初始状态： dp[0]=0，即首日利润为 000 ；
返回值： dp[n−1]，其中 n 为 dp 列表长度。

int maxProfit(vector<int>& prices) {
    int inf = 1e9;
    int minprice = inf, maxprofit = 0;
    for (int price: prices) {
        minprice = min(price, minprice);
        maxprofit = max(maxprofit, price - minprice);
    }
    return maxprofit;
}
}

---------总结到此结束

标签：最大,int,股票,收益,prices,minprice,dp,利润
来源： https://www.cnblogs.com/the-only-flash/p/14468300.html