首页 > 其他分享> > 数理统计14：什么是假设检验，拟合优度检验(1)，经验分布函数

数理统计14：什么是假设检验，拟合优度检验(1)，经验分布函数

2021-02-21 23:33:48 作者：互联网

在之前的内容中，我们完成了参数估计的步骤，今天起我们将进入假设检验部分，这部分内容可参照《数理统计学教程》（陈希孺、倪国熙）。由于本系列为我独自完成的，缺少审阅，如果有任何错误，欢迎在评论区中指出，谢谢！

Part 1：什么是假设检验
Part 2：拟合优度检验
- Section 1：离散型（分布已知）
- Section 2：连续型（分布已知）
附录：
- 1、经验分布函数绘制
- 2、自定义函数pearson.chi2()

Part 1：什么是假设检验

假设检验是一种统计推断方法，用来判断样本与样本、样本与总体的差异是由抽样误差引起还是本质差别造成的。其步骤，其实就是提出一个假设，然后用抽样作为证据，判断这个假设是正确的或是错误的，这里判断的依据就称为该假设的一个检验。

假设检验在数理统计中有重要的用途，比如：橙子的平均重量是80斤，这就是一个假设。我们怎么才能知道它是对的还是错的？这需要我们对橙子总体进行抽样，然后对样本进行一定的处理，比如计算总体均值的区间估计，如果区间估计不包含80斤，就认为原假设不成立，便拒绝原假设。

当然，由于样本具有随机性，因此我们只是对该假设进行检验而不是证明，也就是说不论假设检验的结果是接受假设还是拒绝假设，都不能认为假设本身是正确的或是错误的。同时，假设的检验也不是唯一确定的，对任何假设都可以有无数种方案进行检验，比如上面的例子，\(95\%\)的区间估计是一种检验，\(99\%\)的区间估计也可以作为检验，\(90\%\)的当然也可以，只要事先确定了即可。

总之，要将实用问题转化为统计假设检验问题处理，一般需要经历以下几个步骤：

明确所要处理的问题，将其转化为二元问题，只能用“是”和“否”来回答。
设计适当的检验，规定假设的拒绝域，即拒绝假设时样本\(\boldsymbol{X}\)会落入的区域范围（当然也可以是统计量会落入的范围，这两个意思是一致的）。
抽取样本\(\boldsymbol{X}\)进行观测，计算需要的统计量的值。
根据样本的具体值作出接受假设或者否定假设的决定。

以下是假设检验问题的一些常用概念：

零假设即原假设，指的是进行统计检验时预先建立的假设，一般是希望证明其错误的假设，用字母\(H_0\)表示。这种区分方式比较玄乎。
备择假设指的是与原假设所相对立的假设，如果我们拒绝了原假设，就意味着需要接受备择假设。
拒绝域指的是我们会在什么时候拒绝原假设，也就是拒绝原假设时样本所属的集合，它是样本空间的一个子集。

在实际生活中，可以作出的假设是多种多样的，对不同的检验问题有不同的方法，我们接下来对其分别进行讨论。

Part 2：拟合优度检验

拟合优度检验指的是如下的检验问题——对于总体\(X\)和已知的分布\(F\)，\(H_0\)：\(X\)的分布为\(F\)。即用\(F(x)\)这个分布函数来拟合样本\(X_1,\cdots,X_n\)，拟合的优良程度如何。

对于拟合优度检验，其检验思想是构造一个统计量\(D\)，这个统计量刻画样本\(\boldsymbol{X}=(X_1,\cdots,X_n)\)与理论分布\(F\)的偏离程度，\(D\)越大代表理论分布\(F\)与样本表现出来的分布越不相符。由于在\(H_0\)成立也就是\(X\)的分布为\(F\)的条件下，\(D\)作为一个统计量具有确定的抽样分布，且这个统计量描述的是拟合的优良程度，自然\(D\)越小说明拟合得越好。因此，我们这样定义拟合优度：在获得\(\boldsymbol{X}\)的情况下计算出\(D\)的观测值\(D_0\)，则拟合优度为

\[p(D_0)=\mathbb{P}(D\ge D_0|H_0). \]

直观地想象拟合优度，由于作为偏离量\(D\)肯定是非负的，所以如果\(D_0\)越小，拟合优度就越大，同时这也代表着样本与理论程度的偏离小，所以拟合优度可以作为理论分布\(F\)是\(X\)的分布的可靠性度量。有了拟合优度之后，如果拟合优度太小，我们就会否定\(H_0\)，否则接受\(H_0\)，这需要一个阈值\(\alpha\)。常常取\(\alpha=0.05\)，如果拟合优度小于\(\alpha\)就否定零假设，不过阈值的设定多少是有些主观的，因此客观的拟合优度往往比接受和否定的二元回答更有价值。

不过，我们现在还没有讨论偏离量具体应该如何定义，并且偏离量的定义方式也可以多种多样，因此我们接下来将分情况讨论拟合优度检验中，偏离统计量\(D\)的定义。

Section 1：离散型（分布已知）

如果\(X\)是离散型随机变量，则可以进一步区分为如下的两种：有限与可列。我们先讨论有限且分布已知的情况。现在，原假设是\(H_0\)：\(X\)服从如下的分布：

\[F:\begin{pmatrix} a_1 & a_2 & \cdots & a_r \\ p_1 & p_2 & \cdots & p_r \end{pmatrix},\quad \sum_{i=1}^r p_i=1. \]

适用于这种情况的检验是Pearson的\(\chi^2\)检验，这是我们所接触的第一个重要检验。以\(\nu_i\)记所有样本中取值为\(a_i\)的个数，称为观察频数，即

\[\nu_i=\#\{j|X_j=a_i\}. \]

如果样本容量为\(n\)，则理论上，应当有以下关系式：

\[p_i\approx \frac{\nu_i}{n},\quad \nu_i\approx np_i. \]

称\(np_i\)为理论频数，如果\(H_0\)成立，则\(|np_i-\nu_i|\)对所有\(i\)都不应该过大，但又不能简单地取\((np_i-\nu_i)^2\)，需要考虑权重问题。Pearson引进如下的统计量，常称为Pearson \(\chi^2\)统计量，为

\[K_n=\sum_{i=1}^r\frac{(np_i-\nu_i)^2}{np_i} \]

这里，使用\(1/np_i\)作为权重的调整值，构造出检验统计量。使用这个权重的原因是Pearson证明的定理：在\(H_0\)成立的条件下，有\(K_n\stackrel{d}{\to }\chi^2_{r-1}\)。由此，如果由样本计算出\(K_n\)的观测值是\(k_0\)，则拟合优度为

\[p(k_0)=\mathbb{P}(K_n\ge k_0|H_0)\approx\mathbb{P}(\tilde\chi^2_{r-1}\ge k_0), \]

这里\(\tilde\chi^2_{r-1}\)指的是服从\(\chi^2_{r-1}\)分布的随机变量，这样拟合优度就可以用\(\chi^2\)分布的分位数表近似地计算。实际应用时，我们不一定需要这么精确的拟合优度，故只要查询阈值\(\alpha\)对应的分位数值\(\chi^2_{\alpha}(r-1)\)，并比较它与\(k_0\)的大小即可，当\(\chi^2_{\alpha}(r-1)\le k_0\)时拒绝\(H_0\)。

这里，我们以书上的例题为例，介绍如何用R语言计算拟合优度。现在\(n=556\)，

\[\begin{matrix} \nu_i \\ p_i \\ np_i \end{matrix}\begin{pmatrix} 315 & 108 & 101 & 32 \\ 9/16 & 3/16 & 3/16 & 1/16 \\ 312.75 & 104.25 & 104.25 & 34.75 \end{pmatrix} \]
调用自定义函数pearson.chi2(obersved, prob)，代码见附录。这个函数将返回一个列表，其中我们所需要的是\(\chi^2\)统计量的值和拟合优度，故进行如下调用：
> observed <- c(315, 108, 101, 32)
> prob <- c(9, 3, 3, 1)
> pearson.chi2(observed, prob)

	Pearson chi2 test

The value of K:  0.470024 
p-value:  0.9254259 
Accept.
这里，The value of K是卡方统计量的值，p-value是拟合优度。如果需要进一步使用返回值的其他信息，这个函数会返回一个列表。

如果\(X\)是可列的离散随机变量，则需要对观测进行分组，将其划分为\(r\)个区间，这样就将其转化为有限的情形。具体地，分组需要让每一个组内的理论频数和观察频数都不小于5为宜。

Section 2：连续型（分布已知）

如果理论分布是一个已知的连续型分布，虽然分组法依然可以解决（具体可以参考书本内容），但是不论如何取分组间隔，都多少遗漏了信息。对于连续型分布的验证，使用柯尔莫哥洛夫检验（柯氏检验）更为合适。为此，我们需要先介绍经验分布函数。

经验分布函数是一个结合了分布函数的单调、非降、左连续特色的函数，不同的是它可以由样本计算得出。简而言之，经验分布函数就是将经验分布函数中，\(F(x)=\mathbb{P}(X< x)\)的概率变成频率。

注意，苏中根《概率论》中，分布函数的定义是右连续的即\(F(x)=\mathbb{P}(X\le x)\)，而这里经验分布函数的定义却是左连续的。不过，将分布函数定义成左连续或是右连续并不影响使用，我们不妨就遵照左连续的定义。

设\(X_1,\cdots,X_n\)是\(X\sim F\)中抽取的简单随机样本，次序统计量为\((X_{(1)},\cdots,X_{(n)})\)，则\(\forall x\)，定义以下函数为经验分布函数：

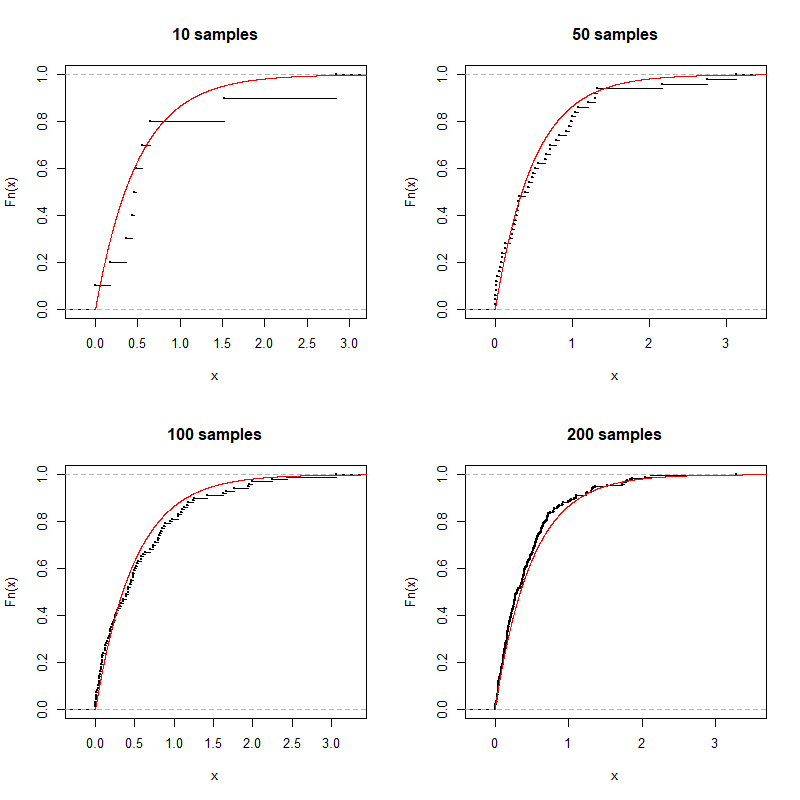
\[F_n(x)=\left\{\begin{array}l 0,& x\le X_{(1)};\\ \frac{k}{n},& X_{(k)}<x\le X_{(k+1)},k=1,\cdots,n-1;\\ 1,& X_{(n)}<x. \end{array} \right. \]

R语言的plot.ecdf函数可以绘制经验分布函数。下面给出一个指数分布的经验分布函数与实际分布函数的示意图：

对于每一个确定的\(x\)，易知

\[F_n(x)=\frac{1}{n}\sum_{i=1}^n I_{-\infty<X_{i}<x}, \]

而

\[\mathbb{P}(I_{-\infty<X_i<x}=1)=\mathbb{P}(X_i<x)=F(x), \]

所以\(F_n(x)\)是一个有限取值的离散型随机变量，有

\[nF_n(x)\sim B(n,F(x)). \]

这样，有\(\mathbb{E}[F_n(x)]=F(x)\)，由强大数定律，\(\forall x\in \mathbb{R}\)，\(F_n(x)\stackrel{\mathrm{a.s.}}\to F(x)\)，即经验分布函数逐点收敛于分布函数。更进一步，如果记\(D_n\)为\(F_n(x)\)与\(F(x)\)的最大偏离，即

\[D_n=\sup_{x\in\mathbb{R}}|F_n(x)-F(x)|, \]

则格里汶科定理保证了

\[\mathbb{P}\left(\lim_{n\to \infty}D_n=0 \right)=1. \]

柯尔莫哥洛夫进一步地证明了以下的结论：

\[\lim_{n\to \infty}\mathbb{P}\left(D_n\le \frac{\lambda}{\sqrt{n}} \right)=K(\lambda),\\ K(\lambda)=\sum_{k=-\infty}^\infty (-1)^ke^{-2k^2\lambda^2},\lambda>0. \]

注意这个\(D_n\)，它显然可以用来描述经验分布与理论分布的偏离程度，因此我们显然可以用它入手来完善拟合优度检验理论。柯氏检验就是建立在经验分布函数基础上的，此时我们取理论分布为\(F\)计算\(D_n=\sup\limits_{x\in\mathbb{R}}|F_n(x)-F(x)|\)，再根据确定的阈值\(\alpha\)，让\(K(\lambda)=\alpha\)找到合适的\(\lambda\)，则检验的临界值就是

\[D_{n,\alpha}=\frac{\lambda}{\sqrt{n}}=\frac{K^{-1}(1-\alpha)}{\sqrt{n}}. \]

由于经验分布函数是阶梯型的，真实的分布函数又是单调的，所以\(D_n\)必定出在各个\(X_i\)的观测值处，具体地有

\[D_n=\max\left\{\left|F_0(x_{(i)})-\frac{i-1}{n} \right|,\left|F_0(x_{(i)})-\frac{i}{n} \right|,\quad \forall i=1,2,\cdots,n \right\}. \]

R语言提供了Kolmogorov-Smirnov检验函数ks.test(x, y)，其中斯米尔诺夫检验适用于检验两组样本是否同分布的。以书上例题为例，可以如下调用：
> num <- c(0.034, 0.437, 0.863, 0.964, 0.366, 0.469, 0.637, 0.632, 0.804, 0.261)  # 书本误将0.437打成了0.0437，可以在底下的计算表中看出
> ks.test(num, qunif)

	One-sample Kolmogorov-Smirnov test

data:  num
D = 0.166, p-value = 0.9052
alternative hypothesis: two-sided
如果我们需要验证的已知分布，则ks.test的第二个参数直接用分布的名称即可（采用默认参数，如果不是默认的\(U(0,1)\)或者\(N(0,1)\)则对样本数据作变换）。

今天，我们介绍了拟合优度检验的部分内容，由于篇幅所限，拟合优度检验的剩余部分将放到下一篇文章中介绍。关于Pearson \(\chi^2\)独立性检验的函数，我将其放到附录中，在使用时可以用source()函数访问，也可以直接将函数复制运行。

附录：

1、经验分布函数绘制

rm(list=ls())
dev.off()

opar <- par(no.readonly = T)
x <- seq(0,6,0.001)
y <- pexp(x, rate = 2)
par(mfrow = c(2,2))

plot.ecdf(rexp(10, 2), cex=0.1, main = "10 samples")
lines(x, y, col='red')

plot.ecdf(rexp(50, 2), cex=0.1, main = "50 samples")
lines(x, y, col='red')

plot.ecdf(rexp(100, 2), cex=0.1, main = "100 samples")
lines(x, y, col='red')

plot.ecdf(rexp(200, 2), cex=0.1, main = "200 samples")
lines(x, y, col='red')

2、自定义函数`pearson.chi2()`

pearson.chi2 <- function(x, p, alpha=0.05){
  # x是实际频数，p是概率列表，alpha是阈值
  rt <- list()
  r <- length(x)  # 可能出现的情况
  p <- p / sum(p)  # 归一化概率列表
  n <- sum(x)  # 总数
  np <- n*p  # 理论频数
  rt$observed <- x
  rt$dim <- r
  rt$total.observed <- n
  rt$prob <- p
  rt$expect <- np
  
  K <- 0
  for (i in 1:r){
    K = K + (np[i]-x[i])^2/np[i]
  }
  rt$pearson.chi2 <- K
  p.value <- 1 - pchisq(K, df=r-1)
  rt$p.value <- p.value
  cat("\n\tPearson chi2 test\n\n")
  cat("The value of K: ", K, "\n")
  cat("p-value: ", p.value, "\n")
  if (p.value > alpha){
    cat("Accept.\n")
  }
  else{
    cat("Reject.\n")
  }
  lst <- rt
}

标签：函数,假设,假设检验,优度,检验,分布,拟合,14
来源： https://www.cnblogs.com/jy333/p/statistical_14.html