插头 DP 学习笔记
作者:互联网
插头 DP 学习总结
By Tuifei_oier
作为全世界最后一个学会插头 DP 的 fw,还是很有必要写一篇学习笔记的。
Part 1 基本思路
对于一些特定的 DP 问题,有时我们如果仅仅知道当前的决策阶段难以直接进行转移,需要更进一步的信息,因此产生了状压 DP 这一类方法。
于是,就有一种比较独特的状压方法被从棋盘问题中总结了出来:插头 DP。
插头 DP 一般和棋盘同时出现,并且有着较为明显的特征,因此比较独特,且相对来说变化并不多,类似于数位 DP 这种形式。
总体的思想就是以每个格子为决策阶段,从上到下从左到右进行决策,同时状压一条这样的“轮廓线”来保存某些信息以进行转移,因此也常称为轮廓线 DP。
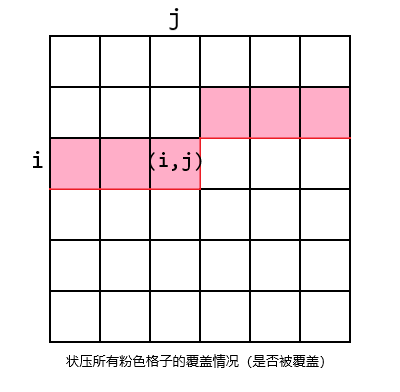
(图片来自这里)
光说不练假把式,还是多做题来积累方法。
Part 2 常见套路
一、覆盖问题
对于一类棋盘覆盖问题的解法,考虑状压轮廓线上格子的覆盖情况,然后考虑即将进入轮廓线的格子的覆盖状态与即将退出轮廓线的格子的覆盖情况来进行转移。
Pro A
给定一个 \(n\times m\) 的棋盘,用 \(1\times 2\) 的方块填满,询问方案数。
考虑直接设置 \(dp_{i,j,S}\) 表示考虑到格子 \((i,j)\),轮廓线上点的覆盖状态为 \(S\) 时的方案数,转移则只需考虑当前格子放竖着的还是横着的或者不放方块即可。为了避免重复同时方便记录状态,规定竖着的方块覆盖当前与上一行的格子、横着的方块覆盖左一列与当前的格子。
一个比较通用的技巧是:将 \(i,j\) 两维滚动,最后一维 \(S\) 由于有用状态少使用 HASH 表。
复杂度为 \(O(nm2^{min(n,m)})\)。
二、连通问题
正是因为这类问题的存在才把插头 DP 叫做插头 DP。
一般来讲,它的大致模型是在棋盘上铺线/选格子使得最终满足某些限制,从中抽象出一个插头的定义。
即,认为一个格子有向某个方向的插头,就是在格子上铺了一条端线在某个方向的线。
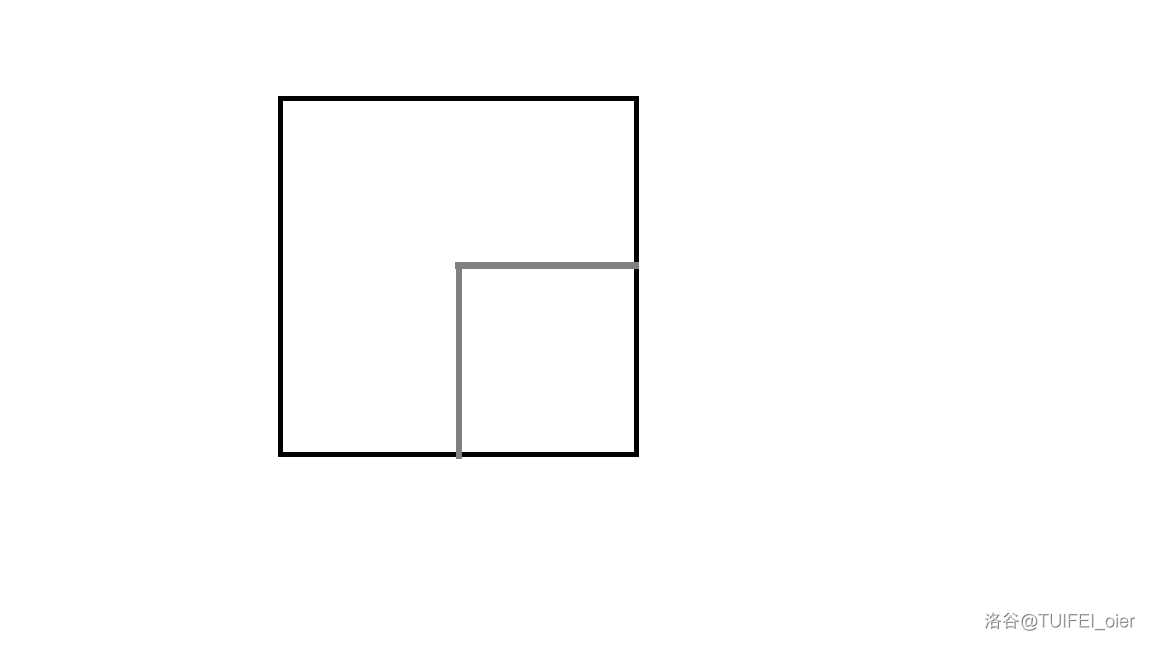
这个格子有一个向下和向右的插头。
所以这种情况下,在一个 \(n\times m\) 的棋盘中,状压的轮廓线实际上是 \(m+1\) 条边上的插头存在情况。
此时已经可以解决一些插头 DP 的经典问题了。
Pro B Eat the Trees
给定 \(n\times m\) 的棋盘,某些格子为障碍不可以铺线,其他格子必须铺线,形成若干个不交叉闭合回路,问方案数。
考虑设 \(dp_{i,j,S}\) 表示考虑到格子 \((i,j)\),轮廓线上插头状态为 \(S\)(\(0\) 为不存在,\(1\) 为存在)的方案数。
转移时,如果当前是障碍,在没有指向当前格子的插头时跳过当前格子即可。
否则,枚举当前格子的铺线情况更新轮廓线即可。
不难发现,只要最后 \(dp_{n,m,S}\) 的轮廓线上没有插头,就是一一对应所有合法的状态。
时间复杂度 \(O(nm2^{min(n,m)})\)。
但是,如果问题再难一点呢?
Pro C 插头 DP
给定 \(n\times m\) 的棋盘,某些格子为障碍不可以铺线,其他格子必须铺线,形成一个闭合回路,问方案数。
这就不能像刚才一样只存插头是否存在了,因为我们不能保证最后全部连通。
此时,一般有两种处理方法:
- 最小表示法。将轮廓线上每个插头与它所在连通块中当前最靠左的插头编号相同。
这样一来,每次修改插头状态直接重新解码再编码即可。 - 括号配对法。发现轮廓线上从左到右 \(4\) 个插头 \(a,b,c,d\) 如果满足 \(a,c\) 连通,\(a,b\) 不连通,则 \(b,d\) 不可能连通。
于是发现连通插头之间不会交叉,且一个连通块在轮廓线上恰好两个插头,想到用括号序列来维护,\(0\) 表示无插头,\(1\) 表示左括号,\(2\) 表示右括号,转移时对应分类讨论即可。
这样就可以解决连通性的问题了,但是第二种方法对于格子而不是插头的问题会失效,此时只能用最小表示法,例如神秘的生物。
Part 3 总结
一般来讲,插头 DP 就这两类主要应用,题目也不是很多,见一种记一种就够了。
练习题:白金元首与莫斯科。
标签:插头,连通,格子,笔记,轮廓线,棋盘,DP 来源: https://www.cnblogs.com/tuifei-oiers-home/p/14346763.html