NOIP2018 提高组题解

Day1-T1 铺设道路

给定一个长为 \(n\) 的数组 \(d\) ，每次可以选择一段连续区间 \([L,R]\) 并全部加一。问最少几次能将整个数组变成 \(0\) .

\(1\leq n\leq 1e5,0\leq d_i\leq 1e4\)

Thoughts & Solution

一个很显然的想法是，如下图将所有的凹陷部分以尽可能连续的横向方块填充：（数据为样例）

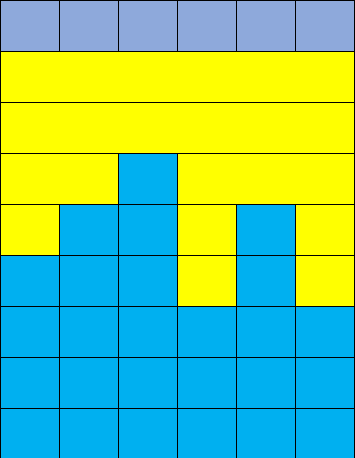
（图中最上面一行为地面，黄色部分每一块就是一次填充）很显然这样就是最优方案。

实现也很简单：从右往左遍历，如果当前 \(a[i]<a[i-1]\) ，就相当于结束掉了上一个横条，不用动；如果当前 \(a[i]>a[i-1]\) ，说明又要新建 \(a[i]-a[i-1]\) 个横条，计入答案即可。

复杂度 \(\mathcal{O}(n)\) .

//Author: RingweEH
int n,las,ans;

int main()
{
    n=read(); las=ans=0;
    for ( int i=1,x; i<=n; i++ )
    {
        x=read();
        if ( x>las ) ans+=(x-las);
        las=x;
    }
    
    printf( "%d\n",ans );

    return 0;
}

Day1-T2 货币系统

有 \(n\) 种不同面值的货币，第 \(i\) 种面值为 \(a[i]\) ，每种无限张。

将一个有 \(n\) 种货币、面值数组为 \(a[1\dots n]\) 的货币系统记作 \((n,a)\) .称两个货币系统 \((n,a),(m,b)\) 等价，当且仅当对于任意 \(x\in N\) ，要么均能被两个货币系统表示出来，要么不能被任何一个表示。

给定一个货币系统 \((n,a)\) ，找到一个最小的 \(m\) 使得存在货币系统 \((m,b)\) 与 \((n,a)\) 等价。

\(n\leq 100,a[i]\leq 25000\) .

Thoughts & Solution

感觉这道题重点不是 DP 是证明……比如你考场的时候，想到了这个解法，但是如果用了怕结论是错的，不用又怕错失正解，其实是很纠结的……所以我这里就写一写证明过程吧，其实也不难。

有一个很显然的想法：答案中的系统方案一定是由原先的系统方案去掉若干种货币得到

事实上这就是正确的。

Proof

令给出的系统中的货币面值为 \(A\) 集合，需要得到的货币面值为 \(B\) 集合。

引理：\(A\) 集合中不能被其他数组成的数一定会在 \(B\) 集合中出现。

引理的证明：设有一个数 \(x\in A\) 且不能被 \(A\) 集合中其他数凑出来。 根据等价，如果 \(x\notin B\) ，那么 \(B\) 中的其他数一定能组成 \(x\) .这就说明 \(B\) 中至少存在一个不属于 \(A\) 集合且不能被 \(A\) 组合出来的数（不然 \(A\) 集合就一定能合成 \(x\) ），那么这个数本身不属于 \(A\) 能组成的范畴，却属于 \(B\) 能组成的范畴，就不符合题意了。所以 \(x\in B\) ,引理正确性证毕。

那么现在我们需要证明：\(B\subseteq A\) .

仍然采用反证法。设存在一个数 \(x\) 满足 \(x\in B\) 且 \(x\notin A\) .

根据题意，显然 \(x\) 能被 \(A\) 中若干个 \(a_1,a_2,\dots ,a_k\) 组成（假定这些数不能被拆分成 \(A\) 中其他的数，如果能拆分就直接拿拆分方案替换即可）。根据引理，这些数都属于 \(B\) ，也就是说，\(B\) 完全可以通过这些数组成 \(x\) ，那么 \(B\) 中再存在一个 \(x\) 显然就是多余的，和 \(B\) 集合最小的要求不符。

Q.E.D.

接下来的事情就非常简单了。我们只需要考虑 \(A\) 集合中哪些数是多余的就好了。

题目暗示：现在网友们打算 简化 一下货币系统。这说明就是在原基础上去掉某些数（

这个事情可以一次 DP 解决。观察到 \(a[i]\) 的范围只有 \(25000\) ，那么可以直接设 \(f[i]\) 表示 \(i\) 这个数能否被前面已经出现过的 \(a[j]\) 组成。

• 如果枚举到 \(a[i]\) 时，\(f[a[i]]=1\) ，那么直接计入答案并跳过即可；
• 如果没有，那么枚举所有的 \(j=a[i]\sim mx\) ，\(f[j]|=f[j-a[i]]\) （就是用 \(j-a[i]\) 和 \(a[i]\) 组成 \(j\) ，枚举范围中的 \(mx\) 表示所有 \(a[i]\) 中的最大值）

完结散花 (｡･∀･)ﾉﾞ

注意题目中给出的 \(a\) 数组不一定有序，要记得排序。

//Author: RingweEH
const int N=110,M=25010;
int n,a[N],f[M];

int main()
{
    int T=read();
    while ( T-- )
    {
        n=read(); 
        for ( int i=1; i<=n; i++ )
            a[i]=read();
        
        sort( a+1,a+1+n ); int mx=a[n];
        memset( f,0,sizeof(f) ); f[0]=1; int ans=n;
        for ( int i=1; i<=n; i++ )
        {
            if ( f[a[i]] ) { ans--; continue; }
            for ( int j=a[i]; j<=mx; j++ )
                f[j]|=f[j-a[i]];
        }

        printf( "%d\n",ans );
    }
}

标签：int,题解,提高,系统,NOIP2018,leq,货币,ans,集合
来源： https://www.cnblogs.com/UntitledCpp/p/14083854.html