arc 045 d 题解
作者:互联网
arc 045 d
首先,有解的充要条件是什么?
若我们将横坐标一样的merge起来,纵坐标一样的merge起来。有解的必要条件是每一个联通块的大小是偶数。那么怎么证明是充分的呢?
我们可以将这些点一层一层的画出来:
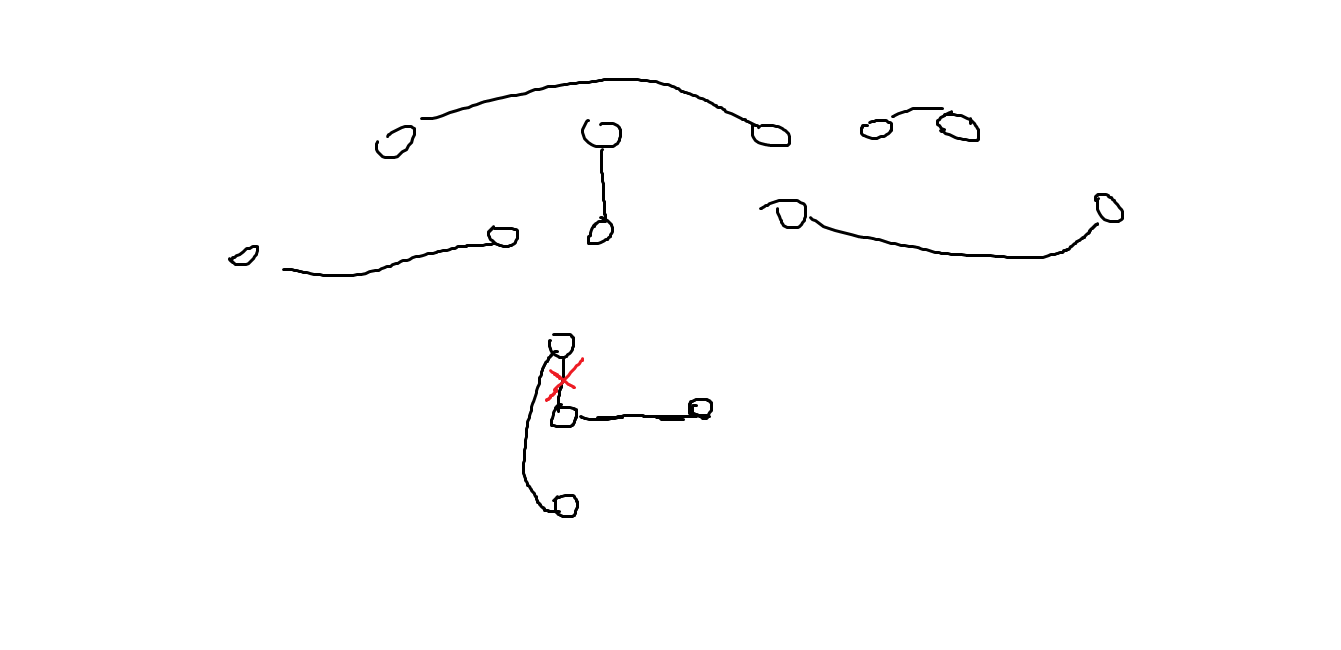
若一行是没有连的点个数是偶数,就直接两两消除。不然就让那个下面有点的剩下来。
不过有一种情况需要注意,就是那个下面有点的和上面连过了(上图的最后四个点)这种情况就将上面的那个移下来。
这样我们可以将点看作边,连接了y行和x列。
这样问题就转化成:删除某一条边,判断剩下的每一个联通块内的边的个数是否都是偶数。
到这里就有了两种做法:
1. 线段树+可撤销并查集
将每一条边出现的时间弄到线段树上。然后一条一条的加边,回退的时候撤销操作。期间用并查集维护连通性,和边的条数。
const int MAXN=100000+20;
bool rest[MAXN*2];
int n,x[MAXN*2],y[MAXN*2];
struct DSU{
int fa[MAXN*4],val[MAXN*4],Rank[MAXN*4];
int cnt;
void init(int N){
rb(i,1,N)
fa[i]=i,val[i]=0,Rank[i]=1;
}
DSU(){cnt=0;}
int root(int u){
if(fa[u]==u) return u;
return root(fa[u]);
}
stack<int> Operation;
stack<mp> Oldval;
void merge(int u,int v){
u=root(u);
v=root(v);
if(u==v){
Operation.push(u);
Oldval.push(II(u,val[u]));
Oldval.push(II(v,val[v]));
return;
}
if(Rank[u]>Rank[v]){
Operation.push(v);
Oldval.push(II(u,val[u]));
Oldval.push(II(v,val[v]));
fa[v]=u;
cnt-=val[v];
cnt-=val[u];
val[u]^=val[v];
cnt+=val[u];
val[v]=0;
}
else{
if(Rank[u]==Rank[v]){
Oldval.push(II(u,val[u]));
Oldval.push(II(v,val[v]));
Operation.push(-v);
Rank[u]++;
fa[v]=u;
cnt-=val[v];
cnt-=val[u];
val[u]^=val[v];
cnt+=val[u];
val[v]=0;
}
else{
Operation.push(u);
Oldval.push(II(u,val[u]));
Oldval.push(II(v,val[v]));
fa[u]=v;
cnt-=val[v];
cnt-=val[u];
val[v]^=val[u];
cnt+=val[v];
val[u]=0;
}
}
}
void add(int u){
u=root(u);
cnt-=val[u];
val[u]^=1;
cnt+=val[u];
}
void undo(){
assert(!Operation.empty());
int v=Operation.top();
if(v<0){
Rank[fa[-v]]--;
}
fa[abs(v)]=abs(v);
Operation.pop();
int X,Y;
X=Oldval.top().FIR;
Y=Oldval.top().SEC;
cnt-=val[X];
val[X]=Y;
cnt+=Y;
Oldval.pop();
X=Oldval.top().FIR;
Y=Oldval.top().SEC;
Oldval.pop();
cnt-=val[X];
val[X]=Y;
cnt+=Y;
}
}dsu;
const int N=1<<18;
vector<mp> tree[N+N];
int Limit;
void add_edge(int u,int v,int a,int b,int now=1,int l=1,int r=N+1){
if(r<=a||l>=b) return ;
if(r<=b&&l>=a){
tree[now].PB(II(u,v));
return ;
}
int mid=(l+r)>>1;
add_edge(u,v,a,b,now<<1,l,mid);
add_edge(u,v,a,b,now<<1|1,mid,r);
}
void run(int now=1,int l=1,int r=N+1){
if(l>2*n+1) return;
for(auto it:tree[now]){
dsu.merge(it.FIR,it.SEC);
}
for(auto it:tree[now]){
dsu.add(it.SEC);
}
if(l==r-1){
rest[l]=(dsu.cnt==0);
}
else{
int mid=(l+r)>>1;
run(now<<1,l,mid);
run(now<<1|1,mid,r);
}
for(auto it:tree[now]){
dsu.add(it.SEC);
}
for(auto it:tree[now]){
dsu.undo();
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=2*n+1;++i){
scanf("%d%d",&x[i],&y[i]);
}
dsu.init(4*n+2);
Limit=2*n+1;
for(int i=1;i<=2*n+1;++i){
if(i!=1)
add_edge(x[i],y[i]+Limit,1,i);
if(i!=2*n+1)
add_edge(x[i],y[i]+Limit,i+1,2*n+2);
}
run();
for(int i=1;i<=2*n+1;++i){
puts(rest[i]? "OK":"NG");
}
return 0;
}
2. 用边双缩点
显然非桥边不会影响连通性,只会影响奇偶性。
桥边会断开某些联通块,这种情况需要记录两边的奇偶性。
yutaka1999:
using namespace std;
typedef long long int ll;
typedef pair <int,int> P;
struct UF
{
int par[SIZE],rank[SIZE];
void init(int n)
{
for(int i=0;i<n;i++)
{
par[i]=i;
rank[i]=0;
}
}
int find(int x)
{
if(par[x]==x) return x;
return par[x]=find(par[x]);
}
void unite(int x,int y)
{
x=find(x);
y=find(y);
if(x==y) return;
if(rank[x]<rank[y])
{
par[x]=y;
}
else
{
par[y]=x;
if(rank[x]==rank[y]) rank[x]++;
}
}
bool same(int x,int y)
{
return find(x)==find(y);
}
};
struct edge
{
int to,id;
edge(int to=0,int id=0):to(to),id(id){}
};
UF uf;
vector <edge> vec[SIZE];
vector <edge> tree[SIZE];
vector <int> nd[SIZE];
int left[SIZE],right[SIZE];
int low[SIZE],ord[SIZE];
int cnt[SIZE];
bool ok[SIZE],use[SIZE],vis[SIZE];
int now_id;
void lowlink(int v,int p=-1)
{
use[v]=true;
low[v]=ord[v]=now_id++;
for(int i=0;i<vec[v].size();i++)
{
edge e=vec[v][i];
if(e.to!=p)
{
if(!use[e.to])
{
lowlink(e.to,v);
low[v]=min(low[v],low[e.to]);
}
else
{
low[v]=min(low[v],ord[e.to]);
}
}
}
}
bool bridge(int s,int t)//true なら橋
{
if(ord[s]>ord[t]) swap(s,t);//ord[s]<=ord[t]
return low[t]>ord[s];
}
void dfs(int v,int p=-1)
{
vis[v]=true;
for(int i=0;i<nd[v].size();i++) ok[nd[v][i]]=true;
for(int i=0;i<tree[v].size();i++)
{
edge e=tree[v][i];
if(e.to!=p)
{
dfs(e.to,v);
cnt[v]+=cnt[e.to]+1;
if(cnt[e.to]%2==0) ok[e.id]=true;
}
}
}
int sz(int v,int p=-1)
{
vis[v]=true;
int ret=cnt[v];
for(int i=0;i<tree[v].size();i++)
{
edge e=tree[v][i];
if(e.to!=p)
{
ret+=sz(e.to,v);
ret++;
}
}
return ret;
}
int main()
{
int n;
scanf("%d",&n);
for(int i=0;i<2*n+1;i++)
{
int x,y;
scanf("%d %d",&x,&y);x--;y--;
left[i]=x,right[i]=y+2*n+1;
vec[left[i]].push_back(right[i]);
vec[right[i]].push_back(left[i]);
}
for(int i=0;i<2*(2*n+1);i++)
{
if(!use[i])
{
lowlink(i);
}
}
uf.init(4*n+5);
for(int i=0;i<2*n+1;i++)
{
if(!bridge(left[i],right[i]))
{
uf.unite(left[i],right[i]);
}
}
for(int i=0;i<2*n+1;i++)
{
if(bridge(left[i],right[i]))
{
int l=uf.find(left[i]);
int r=uf.find(right[i]);
tree[l].push_back(edge(r,i));
tree[r].push_back(edge(l,i));
}
else
{
int v=uf.find(left[i]);
nd[v].push_back(i);
cnt[v]++;
}
}
int ct=0,pos=-1;
for(int i=0;i<2*(2*n+1);i++)
{
if(!vis[i]&&uf.find(i)==i)
{
if(sz(i)%2==1)
{
ct++;
pos=i;
dfs(i);
}
}
}
if(ct>1)
{
memset(ok,false,sizeof(ok));
}
for(int i=0;i<2*n+1;i++)
{
if(ok[i])
{
puts("OK");
}
else
{
puts("NG");
}
}
return 0;
}
标签:cnt,val,int,题解,Oldval,arc,push,045,SIZE 来源: https://www.cnblogs.com/gary-2005/p/14078918.html