尝试运用普吕克坐标解决三维空间内三角形和线段的相交判断问题
作者:互联网
最近在做一个3D模型布尔运算相关的工程。因为模型是靠三角形面片拼合而成的,所以需要一种算法解决三维空间内三角形和线段的相交判断问题。有幸能在外网搜到了这个文章,其中详细介绍了如何利用普吕克坐标来实现对三角形和线段的相交判定,甚至还包括了直线对三角形、线段对线段、直线对直线的判定,算法实现简单,特此翻译并记录,用以备忘。
知识储备
三角形相交种类
首先来思考一下三角形和线段相交有多少种情况:
| 从三角形角度 | 从线段角度 | ||
|---|---|---|---|
| 非共面情况 | 共面情况 | ||
| 不相交 | |||
| 线段交于三角形一个点 | 三角形经过线段一个端点 | ||
| 交于三角形一边 | 三角形穿过线段内部 | ||
| 线段穿过三角形内 | 线段穿过三角形两边 | ||
| 线段和三角形一边重合 | |||
| 线段穿过三角形一个边一个顶点 | |||
普吕克坐标(Plücker Coordinates)
网络上可以百度的内容中的普吕克坐标,大多都是指用d和m两个参数来表示三维欧几里得空间中的有向直线。
其中d是直线的方向向量,决定了直线的方向;而m是直线上两个点与坐标原点形成的两个向量的叉乘,也就是在数值上等于以这两个向量为邻边画出的平行四边形的面积。而由于可以根据d来计算出这直线上两个点的距离,那么,
m=平行四边形的面积=直线上两点距离*直线到坐标原点距离。也就是说,d和m一个确定了直线的方向,一个确定了直线到原点的距离;并且按照叉乘结果是平面法向量的定义,m确定了直线和坐标原点所在的平面。综合以上,可以唯一确定三维空间里的一条直线。(以上是我自己的个人理解,不知道对不对)
六元组表示法
而在文章中使用到的不是d和m,而是普吕克坐标的另一种表示方法:L = (L[0], L[1], L[2], L[3], L[4], L[5])。
首先假设有两个直线上面的点 p = (px, py, pz) and q = (qx, qy, qz)。根据如此构造一个2*4矩阵:
而六元组的每个参数都等于这个矩阵的2*2子矩阵行列式。也就是说:
\[L[0] = p_x q_y - q_x p_y \\ L[1] = p_x q_z - q_x p_z \\ L[2] = p_x - q_x \\ L[3] = p_y q_z - q_y p_z \\ L[4] = p_z - q_z \\ L[5] = q_y - p_y \]相交判别算法
假设a[6]和b[6]分别是普吕克坐标表示的两个直线。判断两个直线是否相交的算法如下:
\[side(a,b) = a[0]*b[4] + a[1]*b[5] + a[2]*b[3] + a[3]*b[2] + a[4]*b[0] + a[5]*b[1] \]当且仅当side(a,b)==0时,两条直线平行或相交,也可以说是共面或异面相交。
(不知道这式子怎么来的,结果大于0小于0也没说意义是什么,只说等于0在后面用于判别时好像用处不大……以后有机会去查查)
原文中还提到了利用这个式子来验证直线到普吕克坐标的映射关系:对于一个六元组X,如果:
- side(X,X) = 0 and X[2], X[4] and X[5] 都不是0,那么X可以对应一个三维坐标系中的一条直线
- side(X,X) = 0 and X[2] = X[4] = X[5] = 0,那么它无法对应三维坐标系中的一条直线,或者说对应的是无限远处的一条直线
也就是说直线和普吕克坐标点是单射、一一映射的关系。
算法剖析
非共面情况
首先,文章让我们如图构建直线L2、L3、L4:

L2和L3是穿过线段端点和三角形公共顶点的直线。我们可以如下选择公共顶点:
- 如果线段和三角形是互相穿过或者线和三角形一边相交,那么这个公共顶点可以随便选。
- 如果线段交于三角形其中一点,那么这个公共顶点是其余两个顶点的其中一个。
L2、L3分别是公共顶点和线段两个端点形成的直线,L4是公共顶点对面的边所在的直线。进行如下side运算:
\[s1 = side-operator(L4,L3)\\ s2 = side-operator(L4,L2)\]若s1和s2异号,那么返回判断结果不相交;如果同号,则线段和三角形相交。如果其中一个为0,那么线段其中一个端点在三角形上。
共面情况
如果线段和三角形共面,那么线段所在直线也一定和三角形相交。故问题改变为判定线段和线段相交。
其中有个特殊情况,如果线段和三角形三条边都不相交,那么线段要么完全在三角形外,要么包含在三角形内。

文章中按如图生成一个平面外的点,并因此构造直线L1、L2。问题变成判定直线和三角形不共面时相交
故共面情况时我们要解决两个分问题。
线段和线段相交判断
设l1、l2所在直线为s1、s2。如果能知道直线和线段的相交判断,那么分别对l1和s2、l2和s1进行一次该判断,只有两次判断都为相交时,l1和l2相交。
线段和直线相交判断
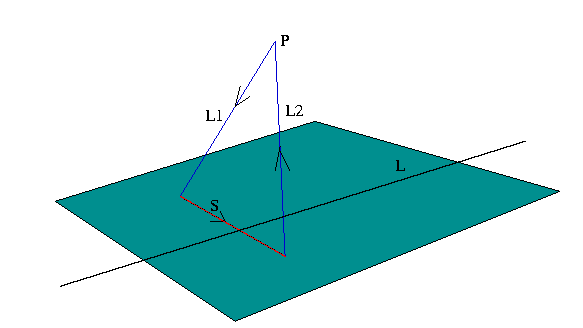
如图构造一个平面外的点,构造直线L1、L2,进行如下side计算:
得到结果对应如下情况:
- s1、s2异号,线段和直线不相交
- s1、s2同号,直线穿过线段
- s1等于s2等于0,线段被包含在直线中
- s1,s2其中一个是0,直线穿过线段一个端点。
判定直线和三角形不共面时相交
令三角形三条边所在直线为e1,e2,e3.进行如下side判断:
\[S1 = side-operator(L,e1)\\ S2 = side-operator(L,e2) \\ S3 = side-operator(L,e3) \]根据我们之前构造的两个直线L1,L2,他们应该都要交于三角形内部,才能最终判定线段包含在三角形内。如图:

它的判断条件是S1、S2、S3同号。
程序设计和实现
函数清单
- 线段和三角形共面判断函数judgeCoplanar()
- 三点共面判断函数judheLine()
- 普吕克生成函数generatePC()
- 普吕克计算函数side()
- 直线和线段判断函数instLineSeg()
- 线段和线段判断函数instSegSeg()
- 主程序接口lineTriIsct()
源码
(暂缺,代码在公司内网电脑里,嘻嘻,加注释一共两百行)
后记
一开始接触到这个普吕克坐标法的时候感觉很稀奇,想着它居然能识别这么多相交情况真是太棒了!结果所有程序都实现回头整理时才发现,包括不相交这个程序只能识别5种:
0. 不相交
- 线段穿过三角形内
- 交于线段一个端点
- 线段被包含于三角形内
- 重合三角形一条边
- 其他种类相交
检查算法原理时发现,在判断线段和线段相交情况时,子问题线段和直线的相交的判断结果被大量丢失,返回的判断结果只剩下"相交"和"不相交"了,这可能是原文存在的一些待改进之处,这让该方法有种大炮打蚊子,而且还打的不准的感觉。如果有机会能更多理解普吕克坐标的原理的话,说不定能让算法变得更完美吧!
标签:直线,线段,相交,普吕克,三角形,side,三维空间 来源: https://www.cnblogs.com/joufulmika/p/14040610.html