3. Distributional Reinforcement Learning with Quantile Regression

C51算法理论上用Wasserstein度量衡量两个累积分布函数间的距离证明了价值分布的可行性，但在实际算法中用KL散度对离散支持的概率进行拟合，不能作用于累积分布函数，不能保证Bellman更新收敛；且C51算法使用价值分布的若干个固定离散支持，通过调整它们的概率来构建价值分布。

而分位数回归(quantile regression)的distributional RL对此进行了改进。首先，使用了C51的“转置”，即固定若干个离散支持的均匀概率，调整离散支持的位置；引入分位数回归的思想，近似地实现了Wasserstein距离作为损失函数。

Quantile Distribution

假设\(\mathcal{Z}_Q\)是分位数分布空间，可以将它的累积概率函数均匀分为\(N\)等分，即\(\tau_0,\tau_1...,\tau_N(\tau_i=\frac{i}{N},i=0,1,..,N)\)。使用模型\(\theta:\mathcal{S}\times \mathcal{A}\to \mathbb{R}^N\)来预测分位数分布\(Z_\theta \in \mathcal{Z}_Q\)，即模型\(\{\theta_i (s,a)\}\)将状态-动作对\((s,a)\)映射到均匀概率分布上。\(Z_\theta (s,a)\)的定义如下

\[Z_\theta (s,a):=\frac{1}{N}\sum_{i=1}^N \delta_{\theta_i(s,a)} \tag{1} \]

其中，\(\delta_z\)表示在\(z\in\mathbb{R}\)处的Dirac函数

与C51算法相比，这种做法的好处：

1. 不再受预设定的支持限制，当回报的变化范围很大时，预测更精确
2. 取消了C51的投影步骤，避免了一些先验知识
3. 使用分位数回归，可以近似最小化Wassertein损失，梯度下降不再有偏

Quantile Approximation

Quantile Projection

使用1-Wassertein距离对随机价值分布\(Z\in \mathcal{Z}\)到\(\mathcal{Z}_Q\)的投影进行量化：

\[\mathcal{\Pi}_{W_1}Z:=\underset{{Z_\theta}\in\mathcal{Z}_Q}{\arg\min}W_1(Z,Z_\theta) \]

假设\(Z_\theta\)的支持集为\(\{\theta_1,...,\theta_N \}\)，那么

\[W_1(Z,Z_\theta)=\sum_{i=1}^N \int_{\tau_{i-1}}^{\tau_i} |F_Z^{-1}(w)-\theta_i|dw \]

其中，\(\tau_i,\tau_{i-1}\in[0,1]\)。论文指出，当\(F_Z^{-1}\)是逆累积分布函数时，\(F_Z^{-1}((\tau_{i-1}+\tau_i)/2)\)最小。因此，量化中点为\(\mathcal{\hat\tau_i}=\frac{\tau_{i-1}+\tau_i}{2}(1\le i\le N)\)，且最小化\(W_1\)的支持\(\theta_i=F_Z^{-1}(\mathcal{\hat\tau_i})\)。如下图

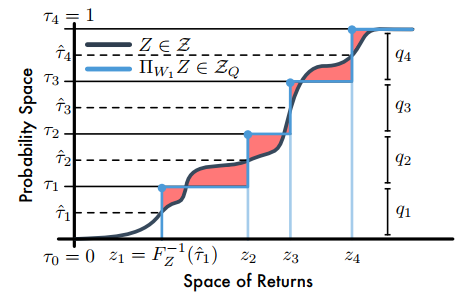
【注】C51是将回报空间(横轴)均分为若干个支持，然后求Bellman算子更新后回报落在每个支持上的概率，而分位数投影是将累积概率(纵轴)分为若干个支持(图中是4个支持)，然后求出对应每个支持的回报值；图中阴影部分的面积和就是1-Wasserstein误差。

Quantile Regression

建立分位数投影后，需要去近似分布的分位数函数，需要引入分位数回归损失。对于分布\(Z\)和一个给定的分位数\(\tau\)，分位数函数\(F_Z^{-1}(\tau)\)的值可以通过最小化分位数回归损失得到

\[\mathcal{L}_{\text{QR}}^\tau(\theta):=\mathbb{E}_{\hat Z\sim Z}[\rho_\tau (\hat Z -\theta)],\quad \text{where} \quad \rho_\tau (u)=u(\tau-\delta_{\{u<0\}}),\forall u\in\mathbb{R} \]

最终，整体的损失函数为

\[\sum_{i=1}^N \mathbb{E}_{\hat Z\sim Z}[\rho_{\hat{\tau}_i} (\hat Z -\theta)] \]

但是，分位数回归损失在0处不平滑。论文进一步提出了quantile Huber loss：

\[\mathcal{L}_{\mathcal{K}}(u)= \begin{cases} & \frac{1}{2}u^2,\quad\quad\quad\quad \text{if} |u|\le \mathcal{K} \\ & \mathcal{K}(|u|-\frac{1}{2}\mathcal{K}),\,\, \text{otherwise} \end{cases} \]

\[\rho_{\tau}^{\mathcal{K}}(u)=|\tau-\delta_{\{u<0\}}|\mathcal{L}_{\mathcal{K}}(u) \]

Implement

QR TD-Learning

QRTD算法(quantile regression temporal difference learning algorithm)的更新

\[\theta_i(s)\leftarrow \theta_i(s)+\alpha (\hat{\mathcal{\tau}}_i-\delta_{\{r+\gamma z^\prime < \theta_i (s) \}}) \]

\(a\sim\pi (\cdot|s),r\sim R(s,a),s^\prime\sim P(\cdot|s,a),z^\prime\sim Z_\theta(s^\prime)\)
其中，\(Z_\theta\)是由公式(1)给出的分位数分布，\(\theta_i (s)\)是状态\(s\)下\(F_{Z^\pi (s)}^{-1}(\mathcal{\hat \tau}_i)\)的估计值。

QR-DQN

QR-DQN算法伪代码

Append

1. Dirac Delta Function

\[\delta_a (x)=\delta (x-a)=0,(x\neq 0) \quad且\quad \int_{-\infty}^\infty \delta_a (x)d_x=1 \]

References

Will Dabney, Mark Rowland, Marc G. Bellemare, Rémi Munos. Distributional Reinforcement Learning with Quantile Regression. 2017.
Distributional RL

标签：tau,Quantile,Distributional,delta,位数,Learning,theta,mathcal,hat
来源： https://www.cnblogs.com/HughCai/p/13862526.html