虽然没有参加这次校赛，但 第一届 总是意义非凡的，要仔细总结！( •̀ ω •́ )✧

---

A

• TAG：签到题

  别问我为什么没有题解，因为不需要题解o(≧口≦)o

A.cpp

#include<cstdio>
int main(){
	puts("tjdl!");
	return 0;
}

---

B

• PZ's solution:

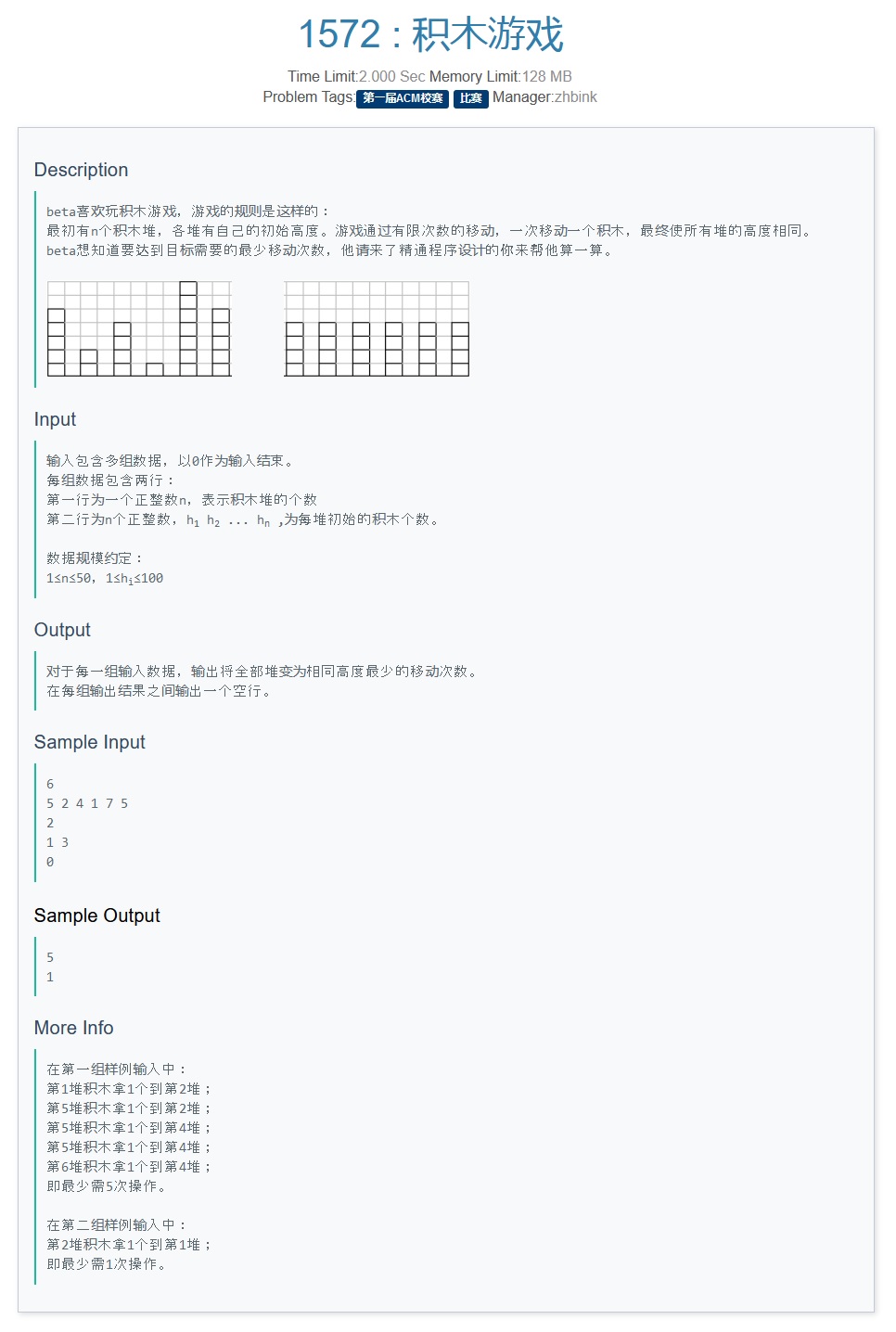
  1. 注意到 一次移动一块积木 ，且目标状态为 所有积木堆的积木数量 均相等，

  可以得到目标 积木堆的积木数量 一定为 \(\frac{\sum_{i=1}^{n}h_{i}}{n}\)即平均值；

  2. 考虑到实际操作时，比平均值多的积木堆的积木 将会移给 比平均值少的积木堆，

  所以实际只有 比平均值多的积木堆 会 对答案有贡献；

  3. 因为目标状态必为 所有积木堆的积木数量 均相等，答案累加的值即为 比平均值多的积木堆的 多于平均值的数量，

  即对第\(x\)堆 积木数量大于平均值的积木堆，其答案贡献为 \(h_{x}-\frac{\sum_{i=1}^{n}h_{i}}{n}\)；

• TAG：模拟；签到题

B.cpp

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,a[55],sum,ans;
int main(){
	while(scanf("%d",&n)&&n!=0){
		sum=ans=0;
		for(int i=1;i<=n;++i) scanf("%d",&a[i]),sum+=a[i];
		sum/=n;
		for(int i=1;i<=n;++i) if(a[i]>sum) ans+=a[i]-sum;
		printf("%d\n",ans);
	}
	return 0;
}

---

C

• PZ's solution：

  

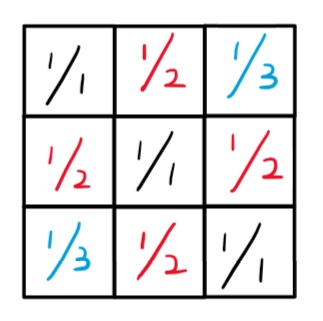
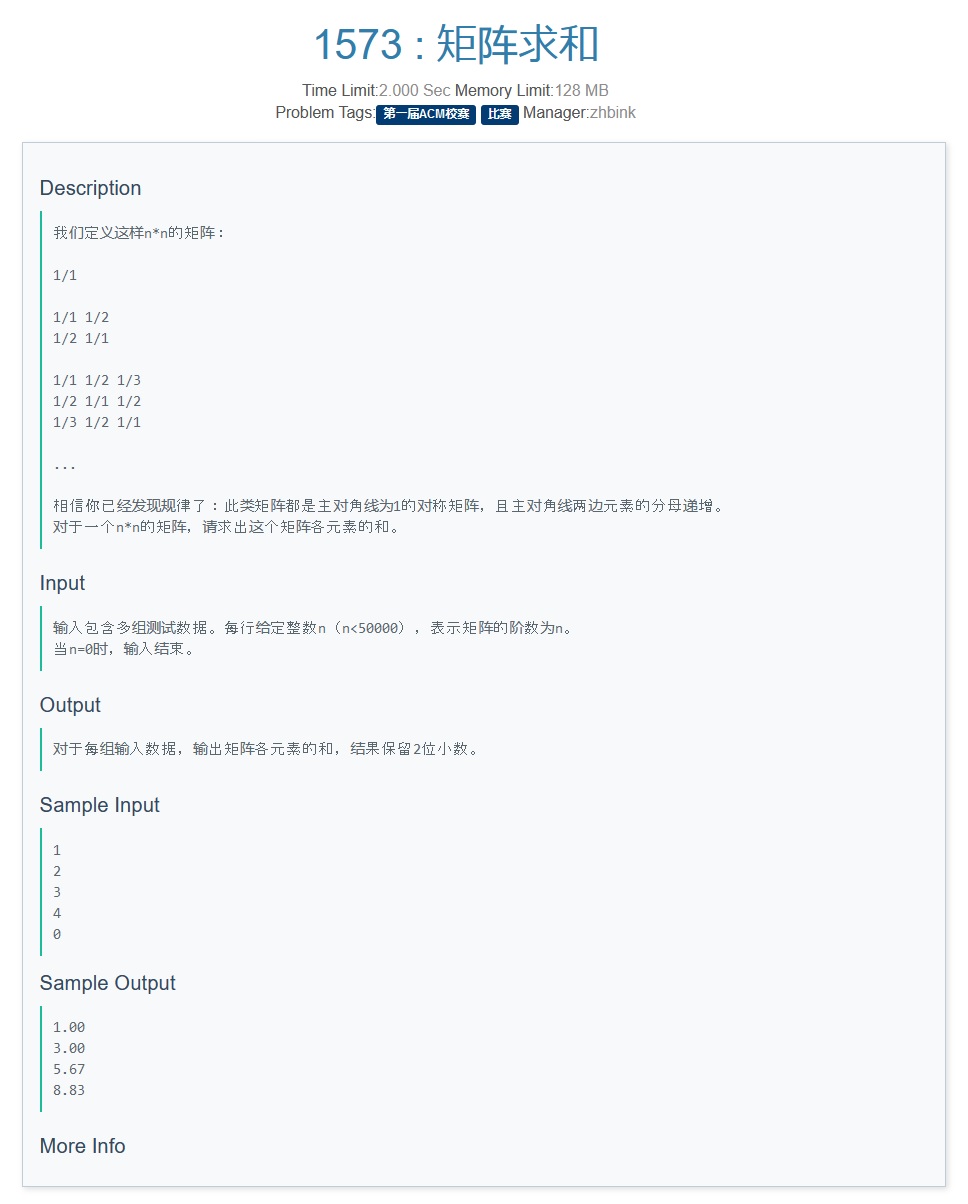
  1. 如图，可以发现矩阵的两个性质：

  (1)矩阵内数值 沿 主对角线 （从左上角到右下角） 对称；

  (2)矩阵内 数值大小 与 数值数量 呈负相关；

  **2. **答案的计算可以从性质(2)入手，我们只观察 矩阵右上方 这一半，

  显然，最小数值必为 \(1/n\) ，而其数量必为 \(1\)；最大数值为 \(1\)，其数量为 \(n\) ；

  **3. **由此我们可以大胆猜想一个关系，即 \(数值1/x的数量为n-x+1\)

• TAG：数学；签到题

C.cpp

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n;
double ans;
int main(){
	while(scanf("%d",&n)&&n!=0){ 
		ans=0;
		for(int i=1;i<n;++i) ans+=i*1.0/(n-i+1.0);
		if(n>1) ans*=2.0;
		ans+=n;
		printf("%.2lf\n",ans);
	}
	return 0;
}

---

D

• TAG：模拟；签到题

  这道题也没有题解，因为题意本身十分明朗，有具体代码实现疑问请见D.cpp╮(╯-╰)╭

D.cpp

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
string s;
int T,n;
void print(char x){ printf("%c",'a'<=x&&x<='z' ? x-'a'+'A' : x); }
int main(){
	scanf("%d",&T); 
	getline(cin,s);
	//T后有一个 '\n' 无法被scanf读取，要提前用
	//getline(cin,s); 读取消掉它! 
	while(T--){
		getline(cin,s);
		n=s.size();
		print(s[0]);
		for(int i=1;i<n;++i)
			if(s[i-1]==' ') print(s[i]);
		putchar('\n');
	}
	return 0;
}

---

E

• PZ's solution：

  **1. **考虑到\(N<2020\)，我们可以使用\(O(N^{2})\)的算法；

  **2. **通过两重循环，寻找 分解成的两个数\(i,j\) ，并可通过计算直接得到 第三个数为\(k=n-i-j\) ；

  3. 我们要在 得到分解出的三个数 的判定时增加一些限制，要保证两点：

  (1)3个数 各不相同；

  (2)此答案 不能重复出现；

• TAG：数学；签到题

E.cpp

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int T,n,ans;
bool check(int x){
	bool f=1;
	while(x){
		if(x%10==2 || x%10==4){ f=0; break; }
		x/=10;
	}
	return f;
}
int main(){
	scanf("%d",&T);
	while(T--){
		scanf("%d",&n);
		ans=0;
		for(int i=1;i<=n;++i)
			for(int j=1;j<i;++j){
				int k=n-i-j;
				if(i>j && j>k && k>0 &&
				   check(i) && check(j) && check(k) ) ++ans;
			}
		printf("%d\n",ans);
	}
	return 0;
}

---

F

• PZ's solution：

  1.考虑使用 \(BFS\) ，判断\(0\)是否 可能 为被围面积的起点，可以通过判断 其上 和 其左 是否为\(1\);

  2.在\(BFS\)过程中，可以发现，不被围起来的\(0\) 一定会遍历到边界，通过此特点判断 无效起点

  3.实现和细节请见代码(¬‿¬)

• TAG：BFS广度优先搜索

F.cpp

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
queue<int>qx,qy;
int fx[]={0,0,1,-1};
int fy[]={1,-1,0,0};
int a[15][15],nx,ny,res,ans;
bool vis[15][15],f;
int  bfs(int x,int y){
	res=0; f=0;
	qx.push(x); qy.push(y); vis[x][y]=1; ++res;
	while(!qx.empty()){
		x=qx.front(); qx.pop();
		y=qy.front(); qy.pop();
		for(int i=0;i<4;++i){
			nx=x+fx[i]; ny=y+fy[i];
			if(vis[nx][ny]||a[nx][ny]==1) continue;
			if((nx==1||nx==10||ny==1||ny==10)&&a[nx][ny]==0){ res=0; f=1; }
			//虽然此处可以判断 非法0起点，但仍让其遍历完所有的0
			//因为我们设置了 vis[x][y] 来表示已经遍历过的点，如果出现 非法边界被遍历过 的情况，就可能无法再 判断非法0起点 了
			if(a[nx][ny]==0&&!vis[nx][ny]&&2<=nx&&nx<=9&&2<=ny&&ny<=9){
				if(!f) ++res;
				vis[nx][ny]=1;
				qx.push(nx); qy.push(ny);
			}
		}
	}
	return res;
}
int main(){
	for(int i=1;i<=10;++i)
		for(int j=1;j<=10;++j)
			scanf("%d",&a[i][j]);
	for(int i=2;i<=9;++i)
		for(int j=2;j<=9;++j)		
			if(a[i][j]==0&&a[i-1][j]==1&&a[i][j-1]==1&&!vis[i][j])
				ans+=bfs(i,j);
	printf("%d",ans);
	return 0;
}

---

G

• PZ's solution：

  1. 首先考虑贪心，对物品的重量\(a_{i}\)进行排序；

  2. 显然， 答案贡献必为 \((a_{i}-a_{i-1})^{2}\) 的形式，即相邻两数的平方差；

  3. 但此时，贪心思想到此结束，因为我们注意到，有一种情况可能存在；

  ！：我们选择 最小的 \(a_{i}-a_{i-1}\) 后，导致 \(a_{i+1}-a_{i-2}\) 及 所有其他答案贡献 极大，造成答案非最优

  **4. **考虑动态规划，设 \(f[i][j]\) 表示 前\(i\)个物品 选了\(j\)对搬走 时的最优答案，

  \(f[i][j]\)可由两个状态转移过来：

  (1)选择搬走\(a_{i}、a_{i-1}\)，此时\(f[i][j]=f[i-2][j-1]+(a_{i}-a_{i-1})^2\)

  (2)选择不搬\(a_{i}\)，此时\(f[i][j]=f[i-1][j]\)

  有状态转移方程

  $$f[i][j]=min(f[i-2][j-1]+(a_{i}-a{i-1})^2,f[i-1][j])$$

• TAG：贪心；动态规划

G.cpp

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<climits>
using namespace std;
int n,m,a[2005],f[2005][2005];
int main(){
	while(scanf("%d %d",&n,&m)&&n!=0){
		memset(f,0x3f,sizeof(f)); 
		for(int i=1;i<=n;++i) scanf("%d",&a[i]);
		sort(a+1,a+1+n);
		for(int i=0;i<=n;++i) f[i][0]=0;
		//初始化可转移的合法状态，即 一对都不选 的状态 
		for(int i=2;i<=n;++i)
			for(int j=1;j<=min(m,i/2);++j)
			//考虑边界，当选择到i时，最多可以选 i/2 对物品,而题目同时也限制最多选m对物品 
				f[i][j]=min(f[i-2][j-1]+(a[i]-a[i-1])*(a[i]-a[i-1]),f[i-1][j]);
		printf("%d\n",f[n][m]);
	}
	return 0;
}

---

H

• PZ's solution：

  1.根据题意，直接考虑 (｡･∀･)ﾉﾞ线段树维护区间最小值；

  2.区间操作 即可视为 区间减 操作；

  其他做法请大家自己探索吧，我会将标程做法也贴在下面

• TAG：线段树；差分；二分答案

H.cpp

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
#define mid (l+r>>1)
#define lo o<<1
#define ro o<<1|1
#define N 1000005
int minx[N<<2],lzy[N<<2],n,m,k,t1,t2,ans;
bool f;
void build(int l,int r,int o){
	if(l==r){ scanf("%d",&minx[o]); return; }
	build(l,mid,lo); build(mid+1,r,ro);
	minx[o]=min(minx[lo],minx[ro]);
}
void pushdown(int o){
	minx[lo]-=lzy[o];
	minx[ro]-=lzy[o];
	lzy[lo]+=lzy[o];
	lzy[ro]+=lzy[o];
	lzy[o]=0;
}
void updata(int l,int r,int L,int R,int k,int o){
	if(lzy[o]) pushdown(o);
	if(f) return;
	if(L<=l&&r<=R){
		if(minx[o]<k){ f=1; return; }
		minx[o]-=k;
		lzy[o]+=k;
		return;
	}
	if(L<=mid) updata(l,mid,L,R,k,lo);
	if(R>mid) updata(mid+1,r,L,R,k,ro);
	minx[o]=min(minx[lo],minx[ro]);
}
int main(){
	scanf("%d %d",&n,&m);
	build(1,n,1);
	for(int i=1;i<=m;++i){
		scanf("%d %d %d",&k,&t1,&t2);
		if(!f){
			updata(1,n,t1,t2,k,1);
			if(f) ans=i;
		}
	}
	printf("%d",ans);
	return 0;
}

std.cpp

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+50;
using ll = long long;
int n,m;
ll a[N],room[N],sum[N],t1[N],t2[N];
 
bool check(int mid)
{
    memset(sum,0,sizeof(sum));
    for (int i=1;i<=mid;i++)
    {
        sum[t1[i]]-=room[i];
        sum[t2[i]+1]+=room[i];
    }
 
    int cnt=0;
    for (int i=1;i<=m;i++)
    {
        cnt+=sum[i];
        if (a[i]+cnt < 0) return 0;
    }
    return 1;
}
int main()
{
    scanf("%d%d",&n,&m);
    for (int i = 1; i <= n; i++)
        scanf("%lld", &a[i]);
    for (int i = 1; i <= m; i++)
        scanf("%lld%lld%lld", &room[i],&t1[i],&t2[i]);
    int l=1, r=m+1;
    while(l < r)
    {
        int mid = (l + r) >> 1;
        if (check(mid)) l = mid+1;
        else r = mid;
    }
    if (l == m+1) {printf("0\n");return 0;}
    printf("%d\n",l);
    return 0;
}

吐槽总结评价

1.这次校赛难度不难，共\(8\)道题，有\(5\)道签到题（在我看来，只要能第一眼看出 做法和细节 的题，都算签到题(*￣3￣)╭）；

2.自己做题的过程中，F题没有注意细节，G题一路贪心到底一直错，H题因为build(1,1,n)的粗心错误一直错，发现自己也是菜的要死。

3.这次比赛的学长我只认识一位ssw，毕竟自己刚来到这里，让我们第二次校赛的题解见，到时候就有自己赛场感受了！

标签：积木,int,ACM,正赛,ans,cpp,using,校赛,include
来源： https://www.cnblogs.com/Potrem/p/SchoolsACM1.html