Luogu6628 [省选联考 2020 B 卷] 丁香之路
作者:互联网
Luogu6628 [省选联考 2020 B 卷] 丁香之路
\(Kruskal\)+欧拉回路
这道题相当妙啊。
本题钦定了起点和终点,容易发现满足题意的路径是一条欧拉路径。欧拉路径的性质是奇点个数为\(0\)或\(2\),在本题中\(s\)和\(i\)恰好是两个奇点,因此剩下的路径上的点的度数应当为\(2\)。
把起点度数和终点度数\(+1\),就转化成了求解欧拉回路(这样实际上\(s\)和\(i\)就是两个奇点了,而其他点均为偶点)。
我们可以把奇点找出来,由于图中路径长度为\(\lvert i-j \rvert\),两点间直接路径最短,我们可以贪心地将相邻的奇点配对连边,使之成为偶点,一条边贡献的度数是\(2\),总度数为偶数,这样的方案一定存在。
但是会出现一个问题,可能我们最终得到的是很多欧拉回路,它们并不连通。
我们可以建立最小生成树将他们连通,边权需要\(\times 2\),因为我们总体需要形成欧拉回路。
建立最小生成树的过程会导致新的连边,这会不会导致答案变劣呢?
比如有四个节点\(A<B<C<D\)(其他中间路程中的点被省略)。
我们的算法会这样连:
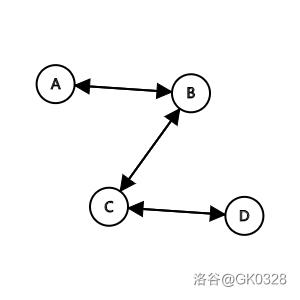
边权和为:\(2(B-A)+2(D-C)+2(C-B)=2D-2A\)。
很容易怀疑以下方式是否更优:
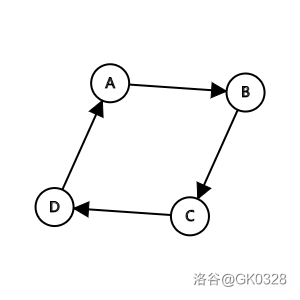
边权和为:\((B-A)+(C-B)+(D-C)+(D-A)=2D-2A\)。
发现我们的计算方式不会让答案变劣。
因此我们证明了这是最优选取方式。
标签:度数,省选,边权,路径,奇点,2020,回路,联考,欧拉 来源: https://www.cnblogs.com/GK0328/p/14018565.html