首页 > 其他分享> > 用线段树演奏跳跃の音符——线段树各类操作相关

用线段树演奏跳跃の音符——线段树各类操作相关

2020-11-21 10:32:24 作者：互联网

线段树也开坑辣qwq，欢迎各位神仙来踩，now我们再来看看菜鸡是怎么从0到1学线段树的吧~

线段树英文$\text{Segment Tree}$，他是一个二叉搜索树，适用于区间修改与查询等相关问题。$1977$年由$\text{Jon Louis Bentley}$发明。

显然，线段树更是一种数据结构，基于分治思想建立一棵储存区间信息的二叉树而来提高操作与查询效率。

聊线段树之前，我觉得应该先学树状数组的相关知识，因为他们俩的相通性太多，作用与思想方面有相似性，而应用范围却又大有不同。如果还没有学过树状数组，可以先去了解并学习一下。

pre芝士:树状数组;

不过我还是多提一下树状数组相关的几个知识点。

树状数组的存储思想也是树，但是存储原理是通过每个位置自身的二进制进行区间划分，是对下标做计算与修改。在根据二进制位给每个位置分层后，会发现就不约而同的形成了一棵树，具体演示可以去百度一下。

线段树与树状数组的复杂度都是$O(logN)$（后面会进行进一步分析），

但线段树相当于树状数组，他有更广的实用性。那么，为什么呢？

树状数组主要维护的是前缀和与差分数组，通过前缀和或者差分数组对区间或点进行查询。前缀和大家都知道，是可以求出区间和的。

公式为：

\[ \displaystyle sum_i = \sum_{j=0}^i a_{j} \]

\[ \displaystyle sum_{[l,r]} = \sum_{i=l}^r a_{i}= \sum_{i=1}^r a_i-\sum_{i=1}^{l-1} a_i=sum_r-sum_{l-1} \]

这样便是前缀和了，区间查询也通过2次前缀和完成，但是这并不是完美的。

千万就不要以为树状数组就可以解决一切区间问题了，前缀和的这类操作仅限于存在逆元运算的时候。当某些区间操作的运算不存在逆元时，就不能通过2次前缀和查询解决区间查询。

在区间操作查询维护方面，~~树状数组没有精神~~，我们线段树，才是你们的-老大哥！

关于区间，有什么不懂的，可以来问我们，我们会，亲切地搞死告诉你们！

树状数组他不行，为什么线段树他却可以？

因为线段树他有明确的二分结构，每个节点就存储着节点的相关信息，通过结合与回溯必然能找到每个节点的相关信息，所以自然可以解决大部分区间问题。

现在我们正式进入线段树的学习

线段树的区间修改与查询

我们提过线段树的节点是存储区间信息的，那具体怎么搭建呢，我们只需要知道以下几点。

线段树的每个节点都是一个区间，根节点代表整个统计范围。

线段树的叶子节点都代表原区间中每个元素单独的那个元区间，也就是$a_i$

线段树非叶子节点的两个子节点的区间是$[l,mid]$和$[mid+1,r]$,$mid=\lfloor \frac{l+r}{2} \rfloor $

那么如果我们有一颗线段树存储了一个$[1,10]$的区间信息，它应该长这样。

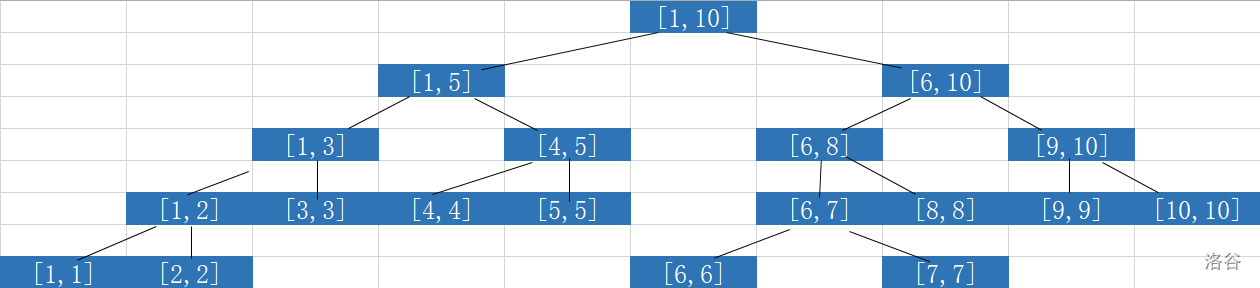
我们来观察一下这颗二叉树，疑似像是一颗完全二叉树？如果我们把叶子节点删除，则保证它是一棵完全二叉树，而对于叶子节点，我们在上面说到他们就代表$a_i$，那么很显然我们在进行操作时几乎不需要考虑他们占用的时间，毕竟对于他们无法继续向下。

那么我们就可以将线段树近似理解为一颗深度为 $\text{log}N$ 的
完全二叉树。

因此，根据这点特性，我们想出了建树的方法。

建树

二叉树是数据结构，虽然采用树的思想，但它并不是严格的图论算法，我们完全没必要去为了它用邻接矩阵或者链式前向星存储。

因为二叉树只有二叉，所以我们可以在一维线性结构中搭建起父子节点的对应关系。

我们设：

根节点编号为1

节点$n$的左子节点编号为$n \times 2$,右子节点为$n \times 2 + 1$。

第$i$层的节点个数对于完全二叉树来说有$2^{i-1}$个。那么我们根节点从1开始可以严格保证每一个空间都被充分利用并且不存在重复使用的空间。因为每一层的第一个节点的编号必定为上一层第一个$\times 2$，那么就都为$2^{i-1}$号，那么最后一个必定是$2^{i-1}+(2^{i-1}-1) = 2^i-1$号，下一个刚好又是下一层第一个，所以保证空间的充分利用。

我们继续来看，一棵线段树存储了$[1,N]$的区间信息，那么必然有$N$个叶子节点，对于有$N$个叶子节点的完美二叉树( $\text{perfect binary tree}$/满二叉树 )，设一共有$m$层，且$2^{m-1}=N$

那么我们必然有

\[ \sum_{i=0}^{m-1} \frac{n}{2^i}=2n-1 \]

个节点，线段树虽然看作是满二叉树考虑，但是最后一层还是有剩余，所以最好我们要给线段树开$4n$的数组大小。

我们在调用一个节点$x$的左右节点时可以直接使用

x<<1和x<<1|1

等价于

x*2和x*2+1 (不熟悉可以手推一下)

所以下面的我的代码中直接用函数

int LS(int x){return x<<1;}

int RS(int x){return x<<1|1;}

前往左右节点。

我们已经分配好了空间，那么怎么获取每个节点存储的相关信息呢。
我们现在给出一个长度$10$的序列，首先显然要给叶子节点们赋上对应值。

~~(好臭的序列）~~

我们现在要求对应区间的最大值，那该怎么建树呢。

显然，对于区间$[l,r]$，$\text{max}_{l,r}=\text{max} ( \text{max}_{l,mid},\text{max}_{mid+1,r})$

且$l=r=i$时，$\text{max}_{l,r}$就是$a_i$

这种自下而上的赋值方法，我们很容易想到递归。

我们从根节点开始向两边子节点分别递归，直到叶子节点赋值为$a_i$开始回溯，回溯时用已经赋值过的2个子节点每次更新自身信息。

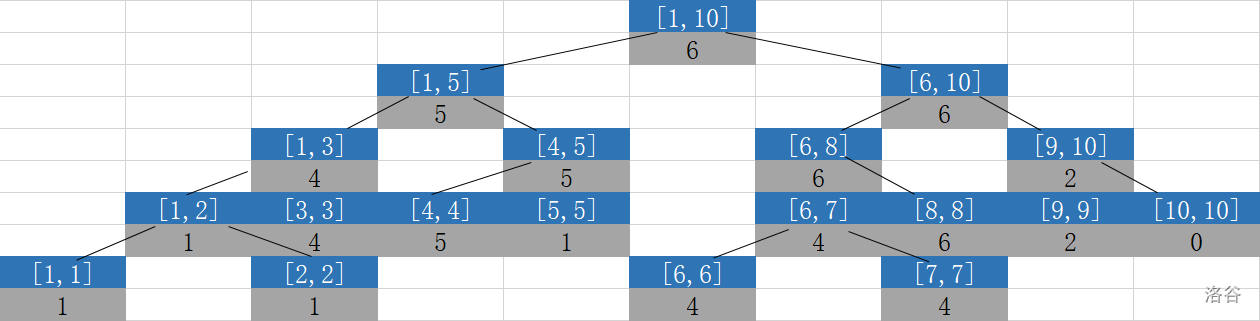
~~最终这棵树变成了光（这样）~~

代码如下

struct Rey
{
	int l,r;
	ll s,laz;
}T[N<<2];
//听说Au选手们都喜欢在函数递归时传递当前左右区间值，
//在更新修改时也是，
//但是一棵树建完后每个节点代表的区间就不变了，
//于是我就直接存储在结构体中方便以后调用（我太懒了）

void UPDATE_sum(int p)
{
	T[p].s=max(T[LS(p)].s,T[RS(p)].s); 
   //线段树维护的信息不同更新的也不同，
   //这里是区间最大值
   //也就是上面我们推出来的左右子区间最大值的的较大值
}

void build(int p,int l,int r)
{
	T[p].l=l,T[p].r=r;//先存好区间端点
	if(l==r){T[p].s=a[l];return;}//叶子节点直接赋值
	int mid=(l+r)>>1;
	build(LS(p),l,mid);//向左节点递归
	build(RS(p),mid+1,r);//向右节点递归
	UPDATE_sum(p); //更新
}

一般的区间查询

区间查询就很显而易见了，对于包括在查询区间内的节点，他的信息一定是备选答案，然后回溯，去跟另外的被完全覆盖的那些区间的备选答案比较选出最佳答案就可以了。

ll VUQ(int l,int r,int p)
{
	ll re=-(1<<30);
	if(l<=T[p].l&&r>=T[p].r)return T[p].s;//完全包括，返回
	int mid=(T[p].l+T[p].r)>>1;
	if(l<=mid)re=max(re,VUQ(l,r,LS(p)));//及时更新
    //左子节点仍然有范围包括在查询区间内
	if(r>mid)re=max(re,VUQ(l,r,RS(p)));
    //右子节点仍然有范围包括在查询区间内
	return re; 
}

单点修改

单点修改很简单，我们简单说一下就好。

我们像建树时那样向下递归，每次判断要修改的那个点在当前节点的左子树还是右子树内。直到走到那个要修改的单点的叶子节点并修改，回溯时顺带更新其到根节点路径上的那些点就行。

代码不贴了，只需要在建树代码中加入对修改节点是在$mid$左还是右的判断即可。

线段树其实根本不怎么考单点修改（吧）

区间修改

这才是重头戏。

顾名思义，区间修改就是对整个区间内的所有数进行同一种操作，如果是不同种那不就是多次单点修改了吗。

区间修改有很多种，一般涉及数值的加减乘除。

如果要对$[l,r]$内每一个节点进行更新，我们承受不住那样的复杂度（$[l,r]$本来被分成$logN$个被完全覆盖的子区间，返回答案也就只需要$O(logN)$,但是以该节点为根的子树上所有节点都需要被修改的情况下，查询就是$O(N)$的复杂度）。于是我们引出新的工具：懒惰标记。（$\text{lazytag}$)

我们不难想到，虽然我们进行的是区间的修改，但是出题人询问答案时候又不一定要求我们输出整个修改过的区间（~~毒瘤坏坏~~）。假设我们对区间$[1,10]$修改，下一次的查询却只查询$[1,5]$，那么我们忙着去更新$[6,10]$就没有必要了。

那么懒惰标记顾名思义，我们就可以将$[6,10]$先不管，在查询时利用懒惰标记先找到$[1,5]$的信息再说，~~反正就是“懒”~~。

那么到底如何实现呢？

我们在更新一个区间$[l,r]$时从根节点开始进行递归，当当前节点代表的区间$[P_l,P_r]$刚好在这个区间内时就打上懒惰标记，我们以区间+6为例，那么$Tag_{P_l,P_r}$就是+6（懒惰标记我们可以在结构体内实现，因为懒惰标记对应的是节点，节点对应区间），一旦到达一个被$[l,r]$完全覆盖的子区间就不用继续往下了，因为如果没用到更下方的那些子区间就很吃亏，需要时再下传懒惰标记就好了。

后续指令中，无论是修改还是查询，我们需要到达$p$的子节点时，我们发现$p$有标记，那么我们就下传这个标记，然后记得清除$p$的标记，毕竟已经下传下去了，就没有重复更新的必要了（不如说根本不能更新两次，那便错了）

其实这个东西挺抽象的。

我们试着画图理解一下

首先我们现在要对区间$[1,4]$进行全体+6的修改。

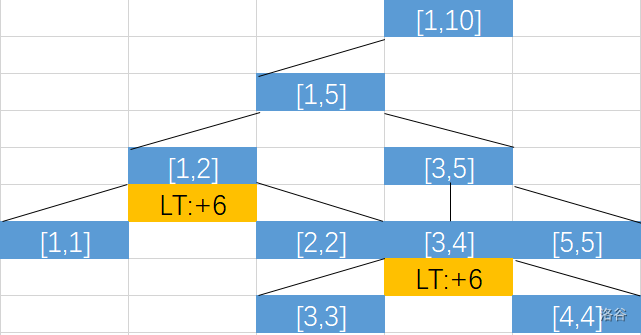
在遍历时我们第一次碰到的被$[1,4]$完全覆盖的节点有2个，也就是$[1,2]$与$[3,4]$，我们给他们打上标记就可以return了，省去处理$4$个叶子节点的时间，这在大数据大范围时很显然是非常优秀的优化。

然后我们又收到了查询$[2,3]$区间的指令，

于是到达$[2,2]$和$[3,3]$的时候，我们判断这是2个被完全覆盖的点，而且在之前的$[1,2]$和$[3,4]$先下传了标记到这$2$个节点。再更新并返回。

对于每个除了修改指令要求范围内那$logN$个节点外的所有子节点的修改都留到下次操作中需要递归到其父亲节点再修改执行。这样免去了不需要的那些区间修改。复杂度也就回归到$logN$。

对于懒惰标记也有对应的注意事项：

懒惰标记不是加上就行的，因为存储的是整个区间信息，所以在下传时要注意是区间值，例如加法懒惰标记就要乘上一个区间长度。
对于多个操作，要注意懒惰标记的优先级，这在P3373 【模板】线段树 2中深有体会。

如果还是很模糊，就来看下代码。

我们分别来看题目P3372 【模板】线段树 1&P3373 【模板】线段树 2的对应代码。

线段树模板1只有区间加法的操作：

void pushdown(int p)
{
	int lf,rt;
	lf=LS(p);rt=RS(p);
	T[lf].s+=(T[lf].r-T[lf].l+1)*T[p].laz;
	T[rt].s+=(T[rt].r-T[rt].l+1)*T[p].laz;
   //加法就是懒惰标记乘上区间长度
	T[rt].laz+=T[p].laz;
	T[lf].laz+=T[p].laz;
   //然后子节点也要更新懒惰标记，万一要求的区间是更小的呢?
	T[p].laz=0; 
   //已经给下面的传过了，于是清除
   
   //对于节点p如果在后续操作中我们需要考虑到其子节点并向下递归
   //那么我们就用这种懒惰标记的下传把之前子节点欠下的补上。
}

void Fix(int p,int l,int r,ll ads)
{
	if(l<=T[p].l&&r>=T[p].r)
	{
		T[p].s+=(ll)(T[p].r-T[p].l+1)*ads;
		T[p].laz+=ads;
     //我们一旦遇到一个完全覆盖在修改区间内的标记就加上懒惰标记
		return ;
     //然后扭头就走，不管子树了。
	}
	pushdown(p);//下传
	int mid=(T[p].l+T[p].r)>>1;
	if(l<=mid)Fix(LS(p),l,r,ads);
	if(r>mid)Fix(RS(p),l,r,ads);
	UPDATE_sum(p); 
    //回溯时仍然记得更新
}

对于线段树2有乘法和加法两种，于是需要考虑优先级：

void Pushdown(int p)
{
	int L=LS(p);
	int R=RS(p);
	T[L].s=(T[p].lazm*T[L].s)%MOD;
	T[L].s=(T[L].s+((T[L].r-T[L].l+1)*T[p].laza))%MOD;
	T[R].s=(T[p].lazm*T[R].s)%MOD;
	T[R].s=(T[R].s+((T[R].r-T[R].l+1)*T[p].laza))%MOD;
	T[L].laza=((T[L].laza*T[p].lazm)%MOD+T[p].laza)%MOD;
	T[R].laza=((T[R].laza*T[p].lazm)%MOD+T[p].laza)%MOD;
	T[L].lazm=(T[L].lazm*T[p].lazm)%MOD;
	T[R].lazm=(T[R].lazm*T[p].lazm)%MOD;
   //我们把上面的过程详细分析一下：
   //因为在下面的代码中，我们会给加法懒惰标记顺势做上乘的处理
   //所以这里我们先乘上再加上那些"已经乘过的"加数
   //这是严格按照分配律来的。
	T[p].lazm=1;
	T[p].laza=0;
	return;
}

void FIX_mul(int p,int l,int r,ll k)//区间乘上k
{
	if(l>T[p].r||r<T[p].l)return;
	if(l<=T[p].l&&r>=T[p].r)
	{
		T[p].s=(T[p].s*k)%MOD;
		T[p].lazm=(T[p].lazm*k)%MOD;
		T[p].laza=(T[p].laza*k)%MOD;
      //为什么加法懒惰标记也要乘上k呢
      //显然，之前如果我们有一个操作是给区间s+x
      //那么后续我们再给这个区间乘上y
      //那么这个区间值应该是(s+x)*y=sy+xy而不是(s*y)+x
		return ;
	}
	Pushdown(p);
	FIX_mul(LS(p),l,r,k);
	FIX_mul(RS(p),l,r,k);
	UPDATE_sum(p);
}

void FIX_add(int p,int l,int r,ll k)
{
	if(l>T[p].r||r<T[p].l)return;
	if(l<=T[p].l&&r>=T[p].r)
	{
		T[p].s=(T[p].s+k*(T[p].r-T[p].l+1))%MOD;
		T[p].laza=(T[p].laza+k)%MOD;
		return ;
	}
	Pushdown(p);
	FIX_add(LS(p),l,r,k);
	FIX_add(RS(p),l,r,k);
	UPDATE_sum(p);
}
//其他都是同理了

带上懒惰标记的区间查询

其实与一般区间查询同理，但是我们要知道，“查询”也是一种操作指令，所以那些被覆盖的节点也算是“被需求”了，于是我们在查询时也要记得在递归前下传懒惰标记保证后面查询正确。

ll VUQ(int l,int r,int p)
{
	ll re=0;
	if(l<=T[p].l&&r>=T[p].r)return T[p].s;
	int mid=(T[p].l+T[p].r)>>1;
	pushdown(p);//下传
	if(l<=mid)re+=VUQ(l,r,LS(p));//改成加上
	if(r>mid)re+=VUQ(l,r,RS(p));
	return re; 
}

~~线段树大概就是这么些个破玩意，于是乎我们完成了大致的线段树学习awa。~~

~~就是太难调了，不然谁不爱呢？~~

博文中所有图均$\textit{made by}$ $\text{EXCEL}$（雾）

其余分析

由于懒惰标记的优势，所以对于每一种区间操作，不论是查询修改，都只需要递归到完全覆盖在查询区间$[l,r]$内的那$logN$个子区间（$N$就是区间长度），所以很明显处理的复杂度都是$O(logN)$

对于网上一些线段树优化的学习，~~其中看起来比较厉害的~~包括标记永久化。

对与一个标记如果保证他对后续值的影响并不会因为特殊条件而改变时（比如说溢出数据范围）我们可以直接将标记打在这个节点上并不清除也不下传，这样保证常数小，在可持久化线段树中可能有使用。

还有就是zkw线段树这个东西，后面会考虑和可持久化线段树一起开坑。

当然，还有非常显然的一点，叶子节点并不需要打懒惰标记，打了也下传不下去，~~所以打了也没啥~~，常数强迫症患者可以特判一下（？）

																基础线段树部分——2020.10.27 写在机房

Reference：

OI Wiki - 线段树部分

李煜东 - 《算法竞赛进阶指南》第$0x43$ & $0x48$节

标签：懒惰,标记,int,线段,节点,区间,跳跃,音符
来源： https://www.cnblogs.com/reywmp/p/14014767.html

用线段树演奏跳跃の音符——线段树各类操作相关

线段树的区间修改与查询

建树

一般的区间查询

单点修改

区间修改

带上懒惰标记的区间查询