信赖域（一）：Cauchy Point与Dogleg

王金戈

从本文开始介绍优化方法的另一大类——信赖域方法。

基本思想

先回顾一下前面几篇文章介绍过的线搜索方法。在线搜索方法的每次迭代中，先确定一个搜索方向，然后沿着该方向寻找一个最佳的步长，使得目标函数在该步长下降得最多。如此迭代下去，直到满足收敛所需的条件。在确定搜索方向时，一般选择梯度下降方向或牛顿方向（即二阶近似的极小值方向）。搜索步长时，一般采用回溯法或back-and-forth方法。

信赖域方法的思路有所不同。在信赖域方法的每次迭代中，先确定一个信赖域半径，然后在该半径内计算目标函数的二阶近似的极小值。如果该极小值使得目标函数取得了充分的下降，则进入下一个迭代，并扩大信赖域半径，如果该极小值不能令目标函数取得充分的下降，则说明当前信赖域区域内的二阶近似不够可靠，需要缩小信赖域半径，重新计算极小值。如此迭代下去，直到满足收敛所需的条件。我们结合下图做进一步的解释。

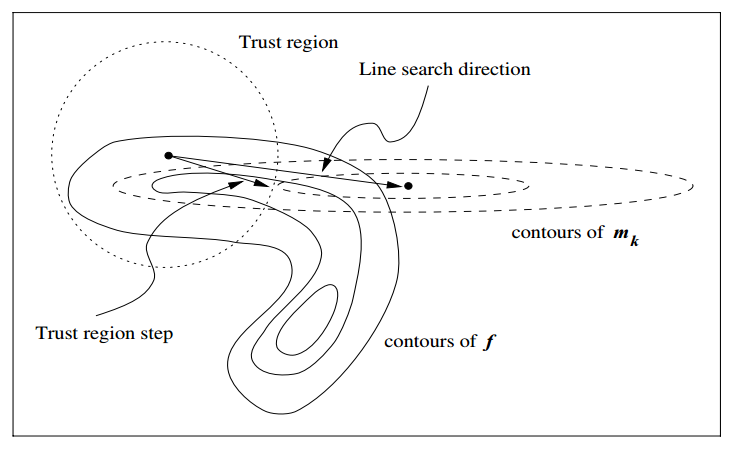
图中，实线表示了目标函数  的等高线，它非常扭曲，因为这样更容易说明信赖域存在的价值。左上的黑点是当前位置，记作  ，即第  次迭代的初始位置。以  为圆心，根据信赖域半径  作圆，得到左上方圆形的信赖域。在  处对目标函数进行二阶近似，得到近似后的二阶函数

其中，  是  处的海森矩阵或近似海森矩阵。在近似后的目标函数中，我们把迭代的步长（含方向）  作为变量，探究当  在信赖域范围内取何值时能够使得  最小。

在二维的情况下，  的等高线是图中椭圆形的虚线。可以看到，在  附近，  还比较接近于  ，但在信赖域以外，它们就差得很远了。  的极小值点更是与  的极小值点差了十万八千里。在这种情况下，如果用线搜索方法中的牛顿法，搜索方向就会直接指向  的极小值点，即图中标出的“Line search direction”。然而，这一方向几乎是与目标函数的等高线平行的，沿着该方向搜索根本无法取得足够的下降。

信赖域方法则好得多，虽然仍旧用  近似目标函数，但在信赖域半径的限制下，我们会找到图中标记为“Trust region step”的向量，该向量正是信赖域范围内使得  最小的步长。显然，此时的  比线搜索方法的结果好得多。

不过，这一现象比较依赖于信赖域半径的选取。可以想象，如果信赖域半径非常大，我们仍然会找到  的极小值点，但此时，这一步长是不能接受的，我们不会进入下一次迭代，而是要重新设置信赖域半径，重新计算步长。那么步长是否可接受的条件是什么呢？定义变量

分母表示目标函数的二阶近似的减小量，分子表示目标函数的减小量。如果  接近于1，说明二阶近似很接近目标函数，这一步长是可以接受的。如果  接近于0甚至小于0，说明二阶近似与真实的目标函数差距较大，我们需要减小信赖域半径，并重新计算步长。

现在，信赖域方法就只剩一个问题了，如何计算  的极小值，即式(4.3)的极小值。直接求当然可以，但也有其它可选方案。根据是否求确切解可以将信赖域方法分为两类，一类是近似方法，只求取信赖域范围内  的近似极小值，适用于问题规模较大，需要节约计算量的情况，另一类是确切方法，计算  更精确的极小值，适用于小规模的问题。本文介绍第一类方法，下篇文章会介绍第二类方法。

Cauchy Point

首先考虑一种最简单的计算  极小值的近似方法。我们固定  的方向为梯度下降方向，沿着该方向寻找位于信赖域内的极小值。即，选择这样的步长

其中

它的含义是，  的方向与梯度下降方向  一致，大小为  。当  时，意味着  是个单调下降函数，所以直接令步长达到信赖域的边界即可，即  。否则，  是个开口向上的二次函数，极小值可以通过令  求得，如果极小值在信赖域内部，则取该步长，否则仍然令步长达到信赖域的边界。

下图展示了这种方法在我们的例子中的效果

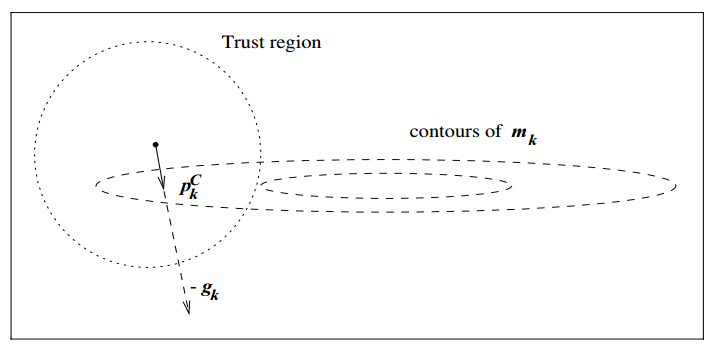
很明显，  的确在梯度下降方向这条线上。事实上，这也是最速下降法应用在信赖域中的最佳结果。但显然这不是最好的结果，  不是信赖域中的极小值点，甚至离极小值点还远得很。但它却有一个响亮的名字——Cauchy Point，之后我们会看到其它算法中都有它的影子，这是其它信赖域方法的基础。另一方面，Cauchy Point方法是最速下降法的一种实现，所以它是全局收敛的，这也奠定了它的基础地位，其它方法只要不差于Cauchy Point方法，就都能保证全局收敛性。

Dogleg

对Cauchy Point的改进，首推Dogleg。

考虑  正定的情况，当  的极小值位于信赖域内时，步长就是牛顿法的解，我们记作  。比较麻烦的是当极小值点位于信赖域外时，你会发现不同的信赖域半径对应的最佳步长的方向都不一样。需要注意的是，这里提到了“最佳步长”，我猜很多人会以为直接求  与信赖域边界的交点就可以了，最初我也是这样想的，但回顾本文的第一幅图，“Trust region step”是所谓的最佳步长，它并非  与信赖域半径的交点。所以，针对不同的信赖域半径求最佳步长是比较困难的，至少没有我们想象的那么容易。

Dogleg方法则提供了一种良好的近似，使得我们可以轻松计算出针对任意信赖域半径的最佳步长。下图展示了Dogleg是如何对真实的最佳步长进行近似的。

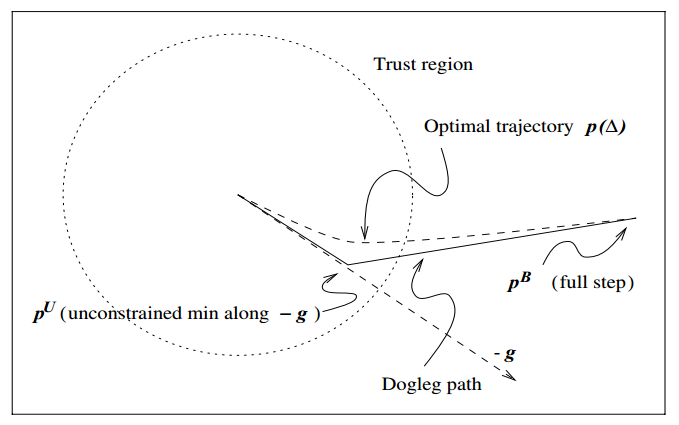
图中“Optimal trajectory”即为真实的最佳步长，它是一条曲线，曲线方程我们无从得知。它的特点是，当信赖域半径很小时，比较接近于Cauchy Point方向，当信赖域半径比较大时，比较接近于无约束的Cauchy Point与  的连线方向。根据这个规律，我们只需要计算出无约束的Cauchy Point  和  ，就能得到两个线段，这就是近似的最佳步长所在的线段。我们把这条折线叫做Dogleg，因为它看起来像一条狗腿。

可以证明，在到达  之前，沿着Dogleg前进，步长的大小是单调递增的，同时  是单调下降的。因此信赖域边界与Dogleg至多有一个交点。在Dogleg方法的每次迭代中，只需要计算给定信赖域半径  对应的最佳步长，然后按照式(4.4)判断是否满足要求，是则进入下一个迭代，否则缩小  再次计算。

改进方案

以上介绍的就是经典的Dogleg方法。在此基础上，还有一种近似程度更高的方法，称为二维子空间最小化（Two-Dimensional Subspace Minimization），这种方法不再是简单地在一条折线上寻找极小值，而是在折线所在的二维平面上寻找极小值，这样就能找到上图中虚线表示的“Optimal Trajectory”。结果会更加精确，但计算量略大于Dogleg，所以实际中并不一定有必要使用这一改进方案。

如果近似海森矩阵  不正定，即存在  的情况，此时  是一个单调下降的函数，也就不存在  ，Dogleg就不适用了。不过我们可以修改近似海森矩阵，使其变得正定，比如用  代替  。可以证明，当  时  正定，其中  是  最小的负特征值。

如果优化变量的规模特别大，导致  的维度非常高，那么无论是用Dogleg还是二维子空间最小化，都涉及到求  或  的步骤，非常耗费计算量。在后面的系列文章中，我们会提到一种迭代求解线性方程的方法——共轭梯度法。共轭梯度法可以经过N次迭代求出N维线性方程的解，而且整个过程不需要对矩阵求逆。把共轭梯度法应用到信赖域方法中，就有了称为CG-Steihaug的方法（CG是共轭梯度的缩写），基本流程与信赖域的流程一致，只不过每次迭代求式(4.3)的极小值时使用共轭梯度法来求，避免矩阵求逆的过程。

这里我们不去深究二维子空间最小化和CG-Steihaug方法的具体细节，因为前者只是对Dogleg的扩展，换一种参数化形式来表示  ，并对式(4.3)应用拉格朗日乘数法，即可求得在信赖域约束下平面上的最小值点，感兴趣的同学可以参考文末的参考资料第一条。后者的主要流程涉及到共轭梯度法的细节，我们会在后续的文章中详细介绍。

参考资料

Derive the solution of the two-dimensional subspace minimization problem in the case where B is positive definite. Guangri Xue

如何理解拉格朗日乘子法？ 马同学

 

上一篇：线搜索（二）：收敛性和收敛速度
下一篇：信赖域（二）：确切方法

编辑于 01-07 数值最优化（书籍） 最优化

标签：Dogleg,Point,近似,步长,Cauchy,信赖,极小值,方法
来源： https://www.cnblogs.com/cx2016/p/13780278.html