快速幂

同余定理

若\(a \% b == c \% b\), 我们称之为\(a\equiv c (\mod b)\)

在四则运算中，我们需要知道

在做题时，我们经常会遇到对一个数取模的运算

我们需要知道

\((a+b)\%c=((a\%c)+(b\%c))\%c\)

\((a-b)\%c=(((a-b)\%c)+c)\%c\)

\((a\times b)\%c=((a\%c)\times(b\%c))\%c\)

对于除法的处理参见下面的逆元

回归正题

快速幂的作用就是以\(O(\log{b})\)的时间复杂度解决\(a^b\%c\)的问题

正常暴力的话我们只能\(O(b)\)

这里用到的是二分的思想

根据上面的同余定理，显然我们可以将问题二分

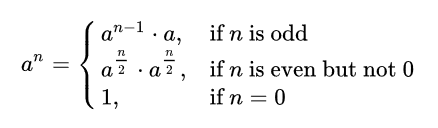
代码的话直接翻译就好啦

LL ksm(LL a, LL n, int c) {
    if (n == 0) return 1;
    else if (n & 1) return (LL)ksm(a, n - 1, c) * a % c;
    else {
        int res = ksm(a, n >> 1, c);
        return (LL)res * res % c;
    }
}

上面的是递归式的，我们也有非递归式的

不妨换个角度思考一下

我们把指数换成二进制

比如我们求\(7^{10}\)

在二进制的角度，也就是\(7^{(1010)_2}\)

所以呢，我们很自然的联想到把它拆分成\(7^{(1000)_2}\)和\(7^{(10)_2}\)

将上面的方法推广，所有的这样的问题我们都可以将指数拆开，分开计算

这样我们需要指数的二进制的每一位，因此，复杂度同上

下面的快速幂也是最常用的快速幂

LL ksm(LL a, LL b, int mod) {
    LL res = 1LL; 
    while(b) {
        if(b & 1) res = (LL)res * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}

逆元

由费马小定理

\(a^p\equiv a (\mod p)\)

\(a^{p-1}\equiv 1 (\mod p)\)

\(a\times a^{p-2}\equiv 1 (\mod p)\)

\(a^{p-2}\equiv \frac{1}{a} (\mod p)\)

因此，a在模c意义下的乘法逆元为\(ksm(a, c - 2, c)\)

还有一种\(O(n)\)线性求逆元的方法

推荐记住推导过程，当然要是直接记住结论也没问题

对于\(i\)在mod p意义下的逆元,我们可以

令\(a=\frac p i, b=p \% i\)

显然p可以表示为\(i\times a + b\)

于是，\(i\times a + b \equiv 0 (\mod p)\)

\(i\times a \equiv -b (\mod p)\)

\(i^{-1} \equiv -\frac a b (\mod p)\)

于是，i的逆元就是\(-a\times b^{-1}\)

即\(-\frac p i \times (p\%i)^{-1}\)

可能你会问，那\(p\%i\)的逆元咋求，用ksm的结论吗？

不难发现，\(p \% i\)肯定比当前的i要小，因此我们再求i的逆元的时候\(p\%i\)的逆元是已知的！

void mutl(int mod) {
    inv[1] = 1;
    for(int i = 2; i <= M; i++) 
    inv[i] = ((-(mod / i) * inv[mod % i]) % mod + mod) % mod; 
} 

慢速乘

在做题中，我们可能会碰到，两个long long的变量相乘的情况

这时候我们要判断，结果是否会炸long long

如果可能会炸，难道我们要写高精度？？？？

完全没有必要，这里由快速幂的形式，我们引入龟速乘

LL msc(LL a, LL b, LL c) {
	LL ans = 0;
	while(b) {
		if(b & 1) ans = (ans + a) % c;
		a = (a + a) % c;
		b >>= 1;
	}
	return ans;

}

矩阵加速

关于矩阵的具体内容详见百度百科

了解了矩阵乘法的运算方式

我们就可以手动构造一个矩阵

比如，以斐波那契数列为例

\(f[n] = f[n - 1] + f[n - 2]\)

不妨构造矩阵
\(\left[\begin{matrix} f[n] & f[n + 1] & f[n + 2] \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix}\right]\)

如果我们称上面的矩阵为第n个矩阵

那么显然第一个矩阵就是
\(\left[\begin{matrix} f[1] & f[2] & f[3] \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix}\right]\)

也即
\(\left[\begin{matrix} 1 & 1 & 2 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix}\right]\)

我们现在的任务便是构造一个矩阵B，使得
\(\left[\begin{matrix} f[n] & f[n + 1] & f[n + 2] \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix}\right]\times B = \left[\begin{matrix} f[n + 1] & f[n + 2] & f[n + 3] \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix}\right] \)

根据矩阵乘法的方式，我们成功获得矩阵B
\(\left[\begin{matrix} 0 & 0 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \end{matrix}\right]\)

代码如下

#include<bits/stdc++.h>
using namespace std;
#define LL long long
LL in() {
	LL x = 0, f = 1; char ch;
	while(!isdigit(ch = getchar()))(ch == '-')&&(f = -f);
    for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
    return x * f;
}
const int mod = 1e9 + 7;
struct matrix {	
	LL a[3][3];
	matrix() {
		for(int i = 0; i <= 2; i++)
			for(int j = 0; j <= 2; j++)
				a[i][j] = 0;
	}
	friend matrix operator * (const matrix &b, const matrix &c) {
		matrix d;
		for(int i = 0; i <= 2; i++)
			for(int j = 0; j <= 2; j++)
				for(int k = 0; k <= 2; k++)
					(d.a[i][j] += ((LL)b.a[i][k] * c.a[k][j])) %= mod;
		return d;
	}
	void rec() {
		for(int i = 0; i <= 2; i++)
			for(int j = 0; j <= 2; j++)
				this->a[i][j] = (i == j);
	}
	matrix ksm(LL t) {
		matrix c;
		c.rec();
		while(t) {
			if(t & 1LL) c = c * (*this);
			(*this) = (*this) * (*this);
			t >>= 1LL;
		}
		return *this = c;
	}
}A, B;
void init() {
	A.a[1][0] = A.a[2][1] = A.a[2][2] = A.a[1][2] = 1LL;
	B.a[0][0] = B.a[0][1] = 1;
	B.a[0][2] = 2;
}
int main() {
	init();
	printf("%lld\n", (B * A.ksm(in() - 1)).a[0][0]);
	return 0;
}

标签：matrix,LL,矩阵,times,逆元,慢速,mod
来源： https://www.cnblogs.com/olinr/p/13303737.html