该篇为Matlab Tech Talk的Trimming and Linearization视频的笔记，原视频见：https://engineeringmedia.com/videos

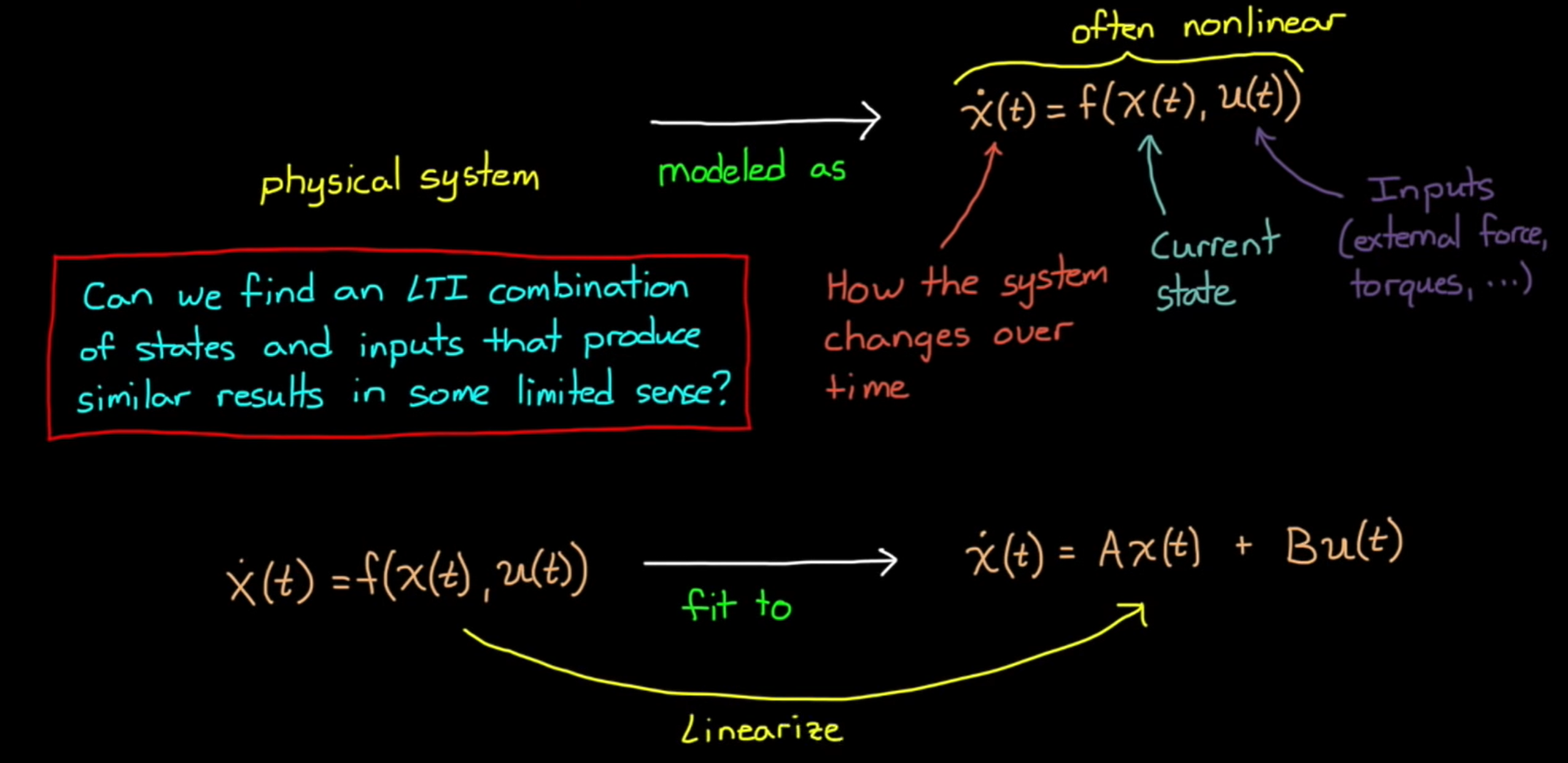
1 什么是线性化

在自然界中很多系统都是非线性的，但是为了方便我们分析，我们需要寻找一个在一定限制条件下有效的线性近似，这个寻找线性近似的过程就是线性化。

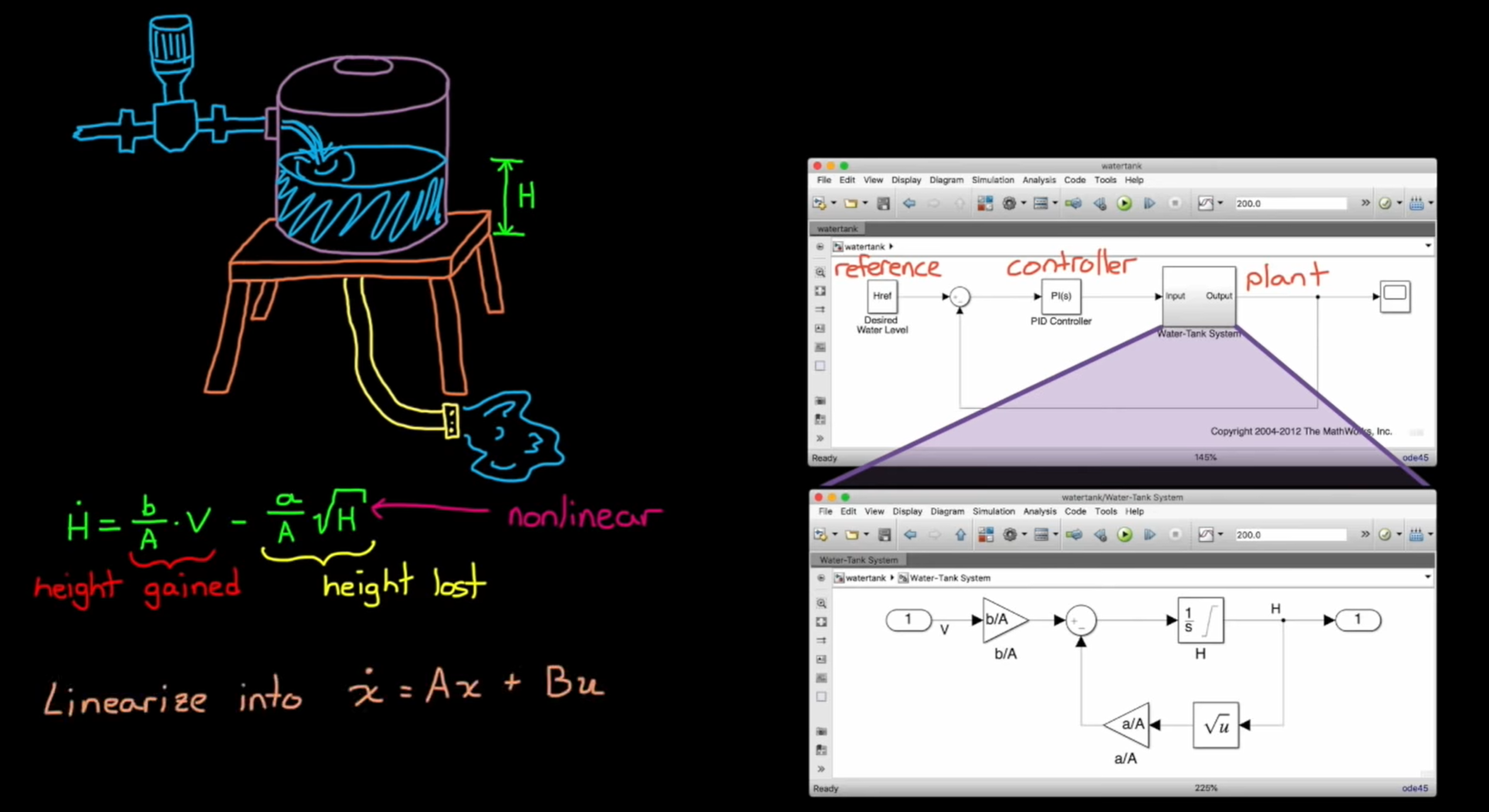
2 水箱系统

Matlab中有一个水箱系统的示例，我们根据水箱系统的Block，可以得到描述这个模型的微分方程。其中 \(\sqrt{H}\) 一项使得这个系统是一个非线性的系统，我们希望将它线性化为一个形如 \(\dot x=Ax+Bu\) 的线性系统。

为什么要花时间精力近似一个线性模型，有以下几点理由：

1. 线性系统的稳定性和具体表现更易于分析
2. 用于线性系统控制器设计的工具更多
3. 仿真速度更快

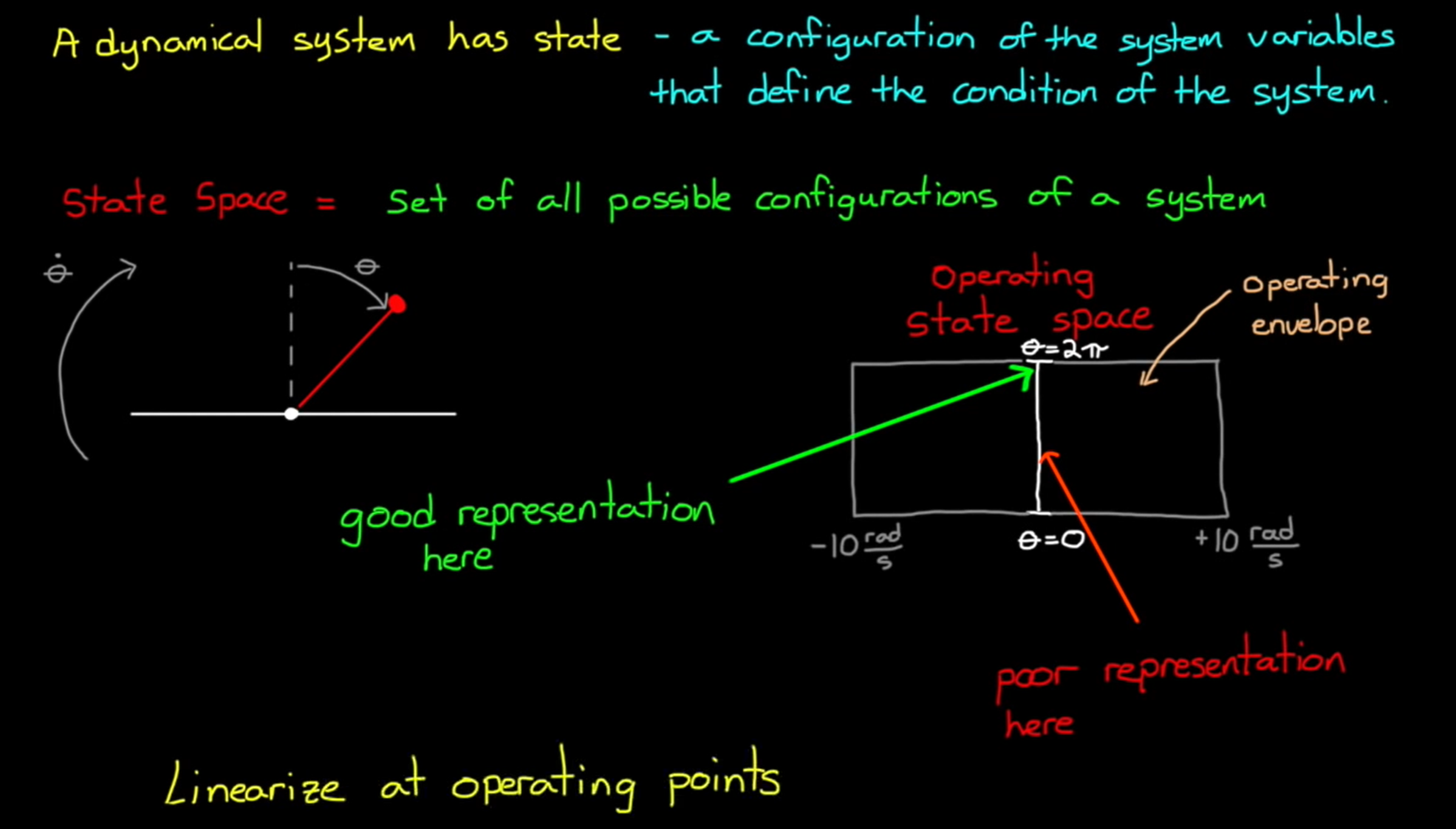
3 系统状态

4 Trimming

5 一个简单的例子

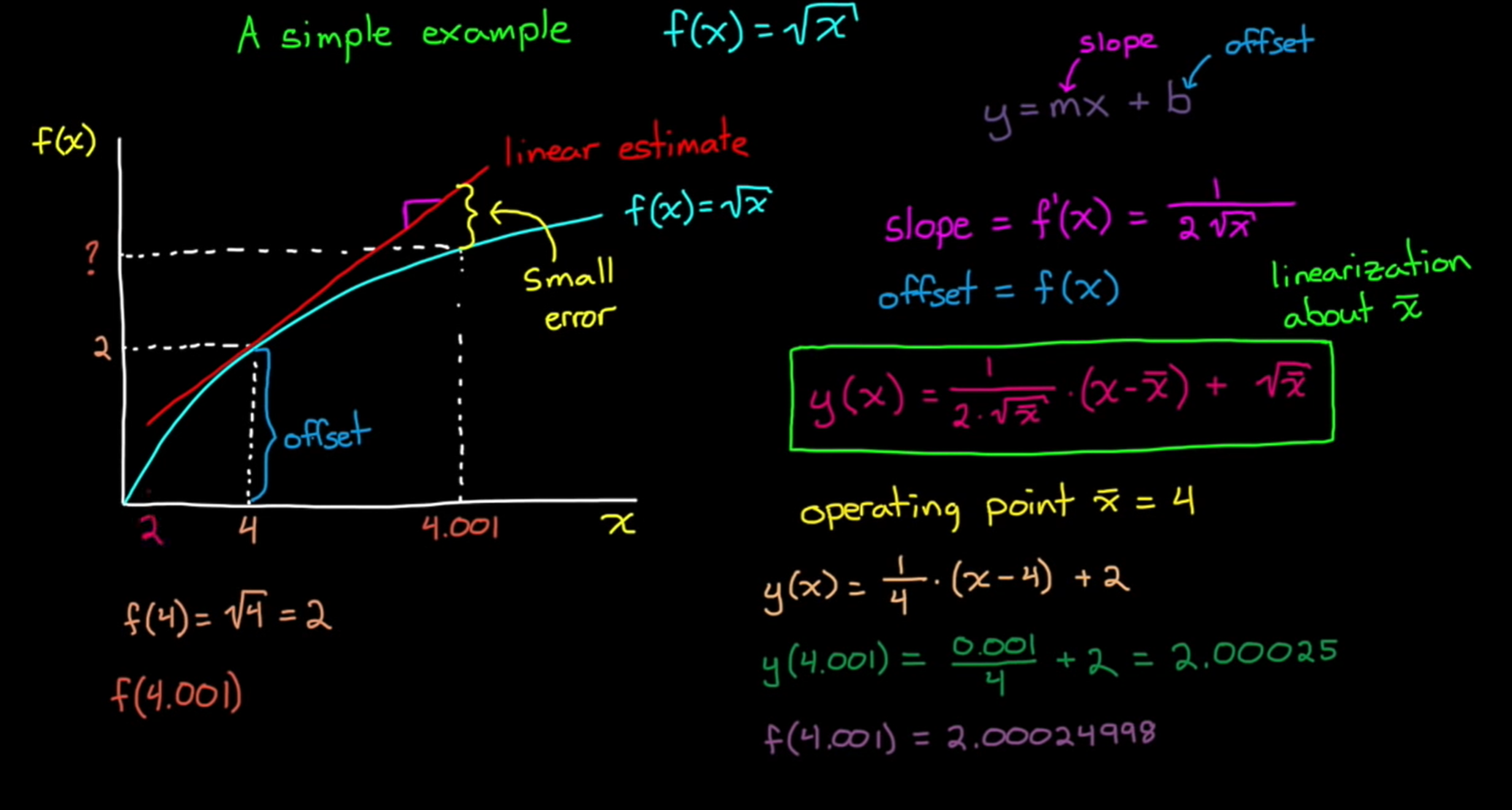
6 回到水箱模型

经过上面的例子，我们知道线性化的大致流程：

1. 首先选取一个operating point \(\bar x\) ，一般来说我们选用系统的稳定点或者临界稳定点或者其他的系统经常处于的点。在这里我们选取 \(\bar x = \bar H = 4\) 。
2. Trimming：如果这个点不是稳定点的话，我们需要调整输入来使系统达到稳定。比如这里我们选的 \(\bar H = 4\) 就不是一个平衡点，因此我们需要调整一个输入值来使系统稳定。通过代入 \(\dot H=0,\bar H = 4\) 我们可以计算出 \(\bar V=\frac{2a}{b}\) 。由于这是一个但输入单输出系统，因此微分方程中 \(H \quad V\) 前是一个1*1的矩阵。
3. Expand as Taylor series：接下来我们对微分方程在（\(\bar H\),\(\bar V\)）处以泰勒级数展开，这里只展开到一阶。由于系统在我们选定的operating point在输入的作用下保持稳定，因此 \(\dot H(\bar H,\bar V)=0\) ，我们为了方便表示暂时不写那两个系数，就得到了这样的式子，经过计算偏导数我们可以求得泰勒展开后的式子。
4. Relabel zero point：最后我们可以重新定义状态为零的点，这样我们就可以把 \(H-\bar H\) 与 \(V-\bar V\) 改写成 \(H \quad V\) 。这样就得到了我们线性化后的结果了：

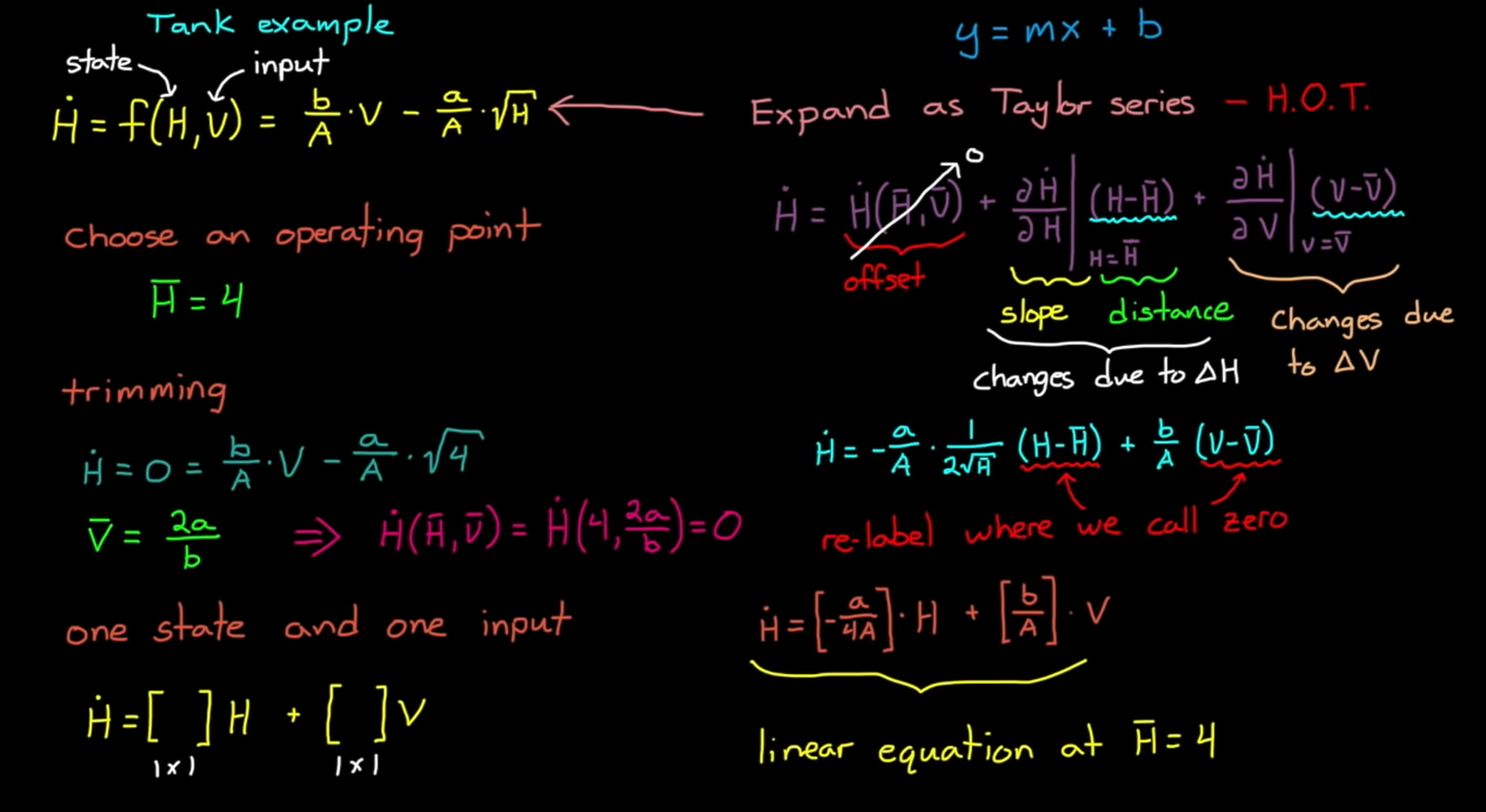
7 其他链接

• Trimming and Linearizing Simulink Models Documentation: http://bit.ly/2E3HzGa

• Linearize Nonlinear Models Documentation: http://bit.ly/2DXWy4G

标签：bar,系统,水箱,线性化,我们,Trimming
来源： https://www.cnblogs.com/HongxiWong/p/12892230.html