【做题笔记】[CSP-J2019]洛谷P5663加工零件

很遗憾2019年没学图论。

否侧这题至少能拿60分。

我谔谔。

首先，一个很容易发现的想法是，设 \(vis_{u,s}\) 表示 \(u\) 号工人是否需要生产一个 \(s\) 阶段的零件，那么一个高达 60 分的程序一下就出来了：

#include <iostream>
#include <stdio.h>
#include <string.h>

int n, m, q, ver[100001], head[1000001], tot, nxt[1000001],vis[1005][1005];

void add(int u, int v)
{
    ver[++tot]=v; nxt[tot]=head[u]; head[u]=tot;
}

void dfs(int u, int s)
{
    if(s==-1 || vis[u][s]) return ;
    //如果 s 为 -1 或 u 已经需要生产一个 s 阶段的零件，直接返回
    vis[u][s]=1;
    //否则 u 工人需要生产一个 s 阶段的零件
    
    for(int i=head[u];i;i=nxt[i])
    {
        int y=ver[i];
        dfs(y,s-1); //与之相连的工人都需要生产一个 s-1 阶段的零件
    }
}

int main()
{
    std::cin>>n>>m>>q;
    for(int i=1;i<=m;i++)
    {
        int u, v;
        std::cin>>u>>v;
        add(u, v);
        add(v, u);
    }

    while(q--)
    {
        int a, L;
        memset(vis, 0, sizeof(vis));
        std::cin>>a>>L;
        dfs(a, L);
        if(vis[1][0]) printf("Yes\n");
        //如果1号工人需要生产一个0阶段的零件就输出Yes
        else printf("No\n");
        //否则输出No
    }

    return 0;
}

接下来考虑正解。注意到一个性质：如果某两个点存在一条传送带，那么这两个点可以互相要零件。把这个性质推广一下：如果1号和另一个工人有一个传送带，那么她们可以互相要零件。

例如下图，2号要生产一个30阶段的零件，那么她就需要向1号要一个29阶段的零件：

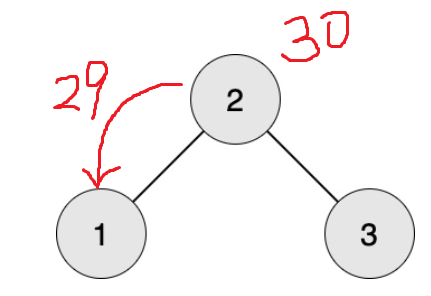
现在，1号要生产一个29阶段的零件，那么她就要向2号要一个28号的零件！

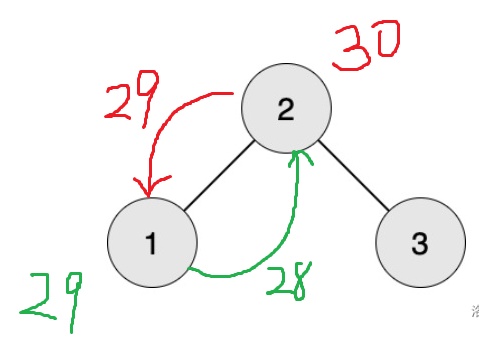
现在，2号要生产一个28阶段的零件，那么她就要向1号要一个27号的零件；1号要生产一个27阶段的零件，那么她就要像2号要一个26阶段的零件......以此类推。

那么我们现在把这个性质稍微抽象一下，也就是说，我们判断1号是否需要向 \(a\) 提供0阶段的零件，只需要看1号是否需要向与之相连的某一号提供0阶段的零件即可！（废话）

接着我们发现：1号点需要向与之相邻（有边）的某一点提供0阶段的零件，当且仅当与之相邻的那一点需要生产一个奇数的零件。

很容易证明其正确性：如果与1号相邻的某一点要生产一个奇数阶段的零件，那么她就必须向1号要一个偶数阶段的零件。而0恰好是一个偶数！

而之所以要大于等于是因为，如果小于，那么就没1号啥事了，在到达一号之前就被别的零件垄断了！

然后我们仔细思考易得：

1. 如果1一定要向 \(a\) 提供一个0阶段的零件，而 \(a\) 需要一个偶数阶段的零件，那么 1~a 的路径中一定存在一条长度为偶数且大于等于这个阶段零件的大小；
2. 如果1一定要向 \(a\) 提供一个0阶段的零件，而 \(a\) 需要一个奇数阶段的零件，那么 1~a 的路径中一定存在一条长度为奇数且大于等于这个阶段零件的大小。

以第一种情况为例解释一下：如果 \(a\) 需要一个偶数阶段的零件，那么只有当某条路径的长度（默认一条边的长度为1）为偶数时，与1号相连的某一点需要生产的零件才为奇数，1号点才要提供一个0阶段的零件！

第二种情况同理。

那么我们是不是真的需要去暴力找边呢？其实不需要。

因为如果有一条最短的路径满足条件，那么与其性质相同的必然也成立（所谓性质相同就是上面提到的两点，因为满足条件的很可能不止一种路径，这时候只要找最短的那条即可！）！

此时，我们就只需要设 \(dis_{u,1}\) 和 \(dis_{u,0}\) 分别表示 1~u 的奇数最短路径和偶数最短路径，然后跑一遍 SPFA ，求出这个最短路，然后判断是否满足即可。一些细节见代码：

#include <iostream>
#include <stdio.h>
#include <queue>

using namespace std;

int n, m, q, tot, head[1000001], nxt[1000001], ver[1000001];
int dis[100001][3], vis[1000010][3];

void add(int u, int v)
{
    ver[++tot]=v; nxt[tot]=head[u]; head[u]=tot;
}

void spfa()
{
    queue<int> q, p;
    //q队列表示点
    //p队列表示奇数或偶数
    for(int i=1;i<=n;i++) dis[i][1]=dis[i][0]=233333333;
    //一开始全部搞成无穷大
    dis[1][0]=0;
    //第一个点本身就是偶数，所以偶数最短路径为0
    //奇数最短路径显然不存在
    q.push(1);
    p.push(0); //一开始push 1 也是可以的
    while(!q.empty()&&!p.empty())
    //必须要两个队列均不为空
    {
        int u=q.front(); q.pop();
        int s=p.front(); p.pop();
        vis[u][s]=0;
        for(int i=head[u];i;i=nxt[i])
        {
            int y=ver[i];
            if(dis[y][0]>dis[u][1]+1)
            {
                dis[y][0]=dis[u][1]+1;
                //偶数边可以通过奇数边+1得到
                if(!vis[y][0])
                {
                    vis[y][0]=1;
                    q.push(y);
                    p.push(0);
                }
            }
            //处理偶数最短路
            if(dis[y][1]>dis[u][0]+1)
            {
                dis[y][1]=dis[u][0]+1;
                //奇数边可以通过偶数边+1得到
                if(!vis[y][1])
                {
                    vis[y][1]=1;
                    q.push(y);
                    p.push(1);
                }
            }
            //处理奇数最短路
        }
    }
}

int main()
{
    cin>>n>>m>>q;
    for(int i=1;i<=m;i++)
    {
        int u,v;
        cin>>u>>v;
        add(u,v);
        add(v,u);
        //无向图，需要反向建边
    }

    spfa();

    if(head[1]==0) dis[1][0]=233333333;
    //如果1号是孤立点那就也没有路径

    while(q--)
    {
        int a,L;
        cin>>a>>L;
        if(L>=dis[a][L%2]) printf("Yes\n");
        //这里用到了一个技巧判断是需要奇数最短路还是偶数最短路，即
        //偶数%2为0，奇数%2为1，所以我们的dis数组才那样表示
        else printf("No\n");
    }

    return 0;
}

标签：P5663,洛谷,int,偶数,vis,阶段,零件,J2019,dis
来源： https://www.cnblogs.com/BlueInRed/p/12617517.html