1 基本概念准备
1.1 扇形计算公式

1.2 二重积分用极坐标表示

 (略去高阶无穷小)
(略去高阶无穷小)
所以 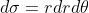
2 高斯分布公式
2.1 高斯概率密度函数的的积分
令 
则
用极坐标表示:

则:

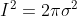
所以:

2.2 高斯分布的期望

令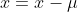
则:

这里 为奇函数,所以积分结果为0
为奇函数,所以积分结果为0
所以:

这里
参考:
高斯分布期望的推导
高斯分布归一化、期望、二阶矩、方差推导证明
标签:期望,推导,所以,公式,积分,极坐标,高斯分布
来源: https://blog.csdn.net/idwtwt/article/details/104715897