计算机组成：数制与运算

数制

注意，补码只是说能让符号位参与运算，并不能让它也同时表示数的大小，理解上不要有偏差

原码表示法

注意这个逗号是用来分割符号位和数值位的，和后面的小数定点机的小数点要区分开，虽然作用是一样的，都是分割符号位

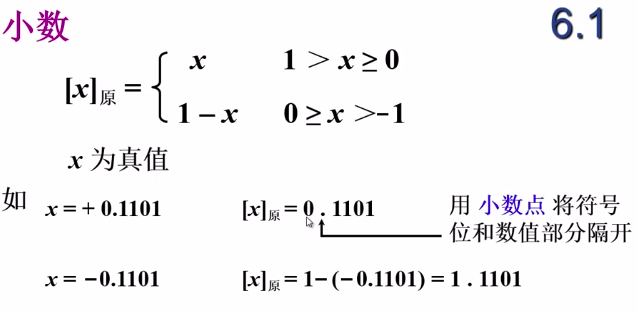
补码表示法

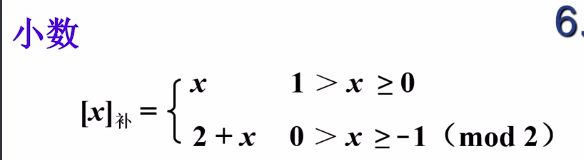
取反加一同样适用于小数的补码：

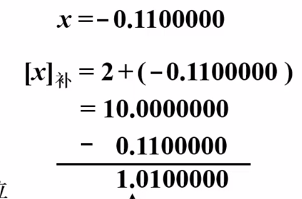
x的相反数是0.1100000，取反为1.0011111，加一是在末尾加一，结果是1.0100000

移码表示法

使用移码的原因:补码很难直接判断其真值大小

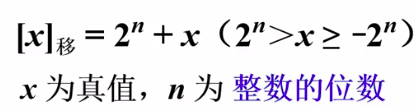
对正数和负数做同样的处理

从数轴上看:

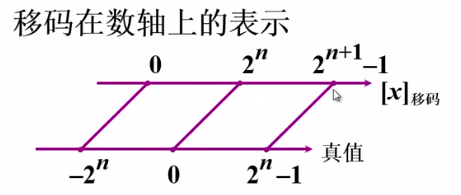
移码通常用来表示浮点数的阶码部分，所以没有小数定义，主要就是图它大小好判断

移码和补码的比较

数的定点表示

在计算机中，没有专门的硬件用来表示小数点，小数点的位置是计算机体系结构设计人员在设计体系结构时约定的

小数定点机只能表示不到[-1,1]的数字，而整数定点机只能表示正负整数

关于取值范围，有这样的解释:

来源：https://www.zhihu.com/question/50758554

一个数用(n+1)位存储，原码（反码）用掉一个符号位后，还有n位，如果小数点在最右边，此时表示的是整数，可表示 这些数，把小数点左移n位，相当于除以 ，结果为：

同理，补码可表示的整数是 ，除以 ，结果为：

这样就可以看明白了，对于小数定点机，由于其数符位是用来表示正负的，所以正数最大就是0.11111111，负数最小就是1.0000000

关于原码、补码和反码的计算：

蓝色是整数定点机，黑色是小数定点机

来源：https://blog.csdn.net/qq_39690706/article/details/85856792

原码
原码的表示方法：

注意，这里2的n次方减去X，是为了让它的符号位为1

简单来说就是，在机器中我们使用0和1来区分一个数的符号，用0来表示正数，用1来表示负数。而原码表示就是将一个数绝对值的二进制表示出来后根据是正数还是负数在前面加0或1表示数的符号。这里注意一点，在定点小数中，原码是不能表示出-1这个值的

反码
反码的表示方法

简单易懂一些的话其实就是如果是正数，X的反码就等于原码，如果是负数，将X的数值位全部取反

补码

定点运算

补码的减法

一个数的负数的补码等于该数的补码取反再加一

原码乘法

这里说的原码运算是可以带符号的

上面的符号位操作是异或

例子：

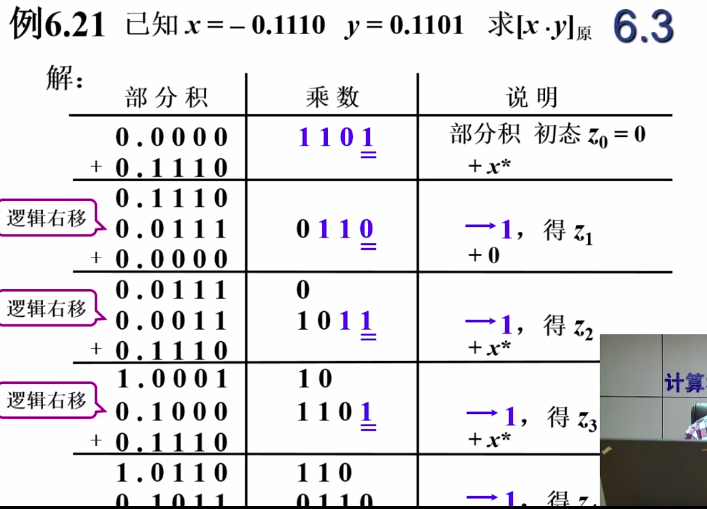
移位都是逻辑移位，也就是直接在前面用0补，而不是循环的

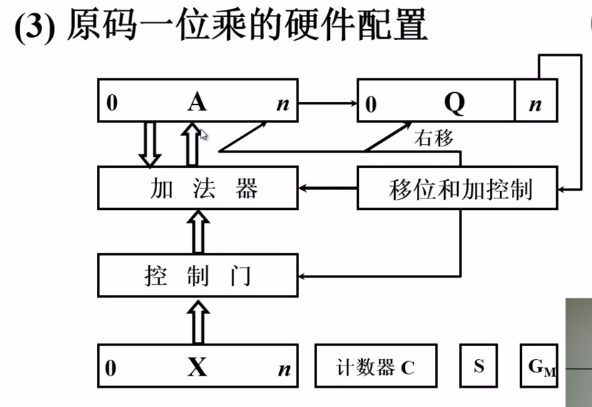
补码乘法

注意这里用的都是小数定点机

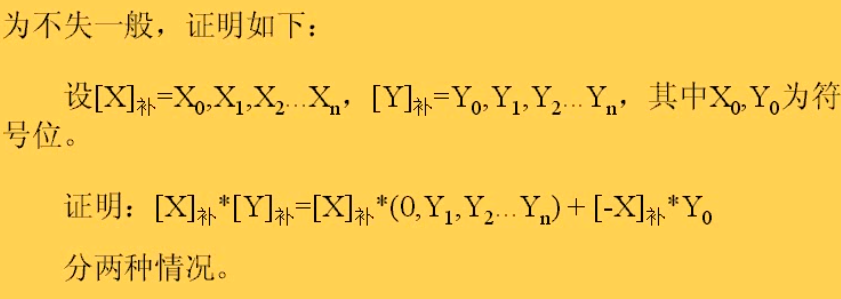
所以说，如果Y0是0的话，补码的运算就可以按照原码的计算方法来(因为后面那个-X项就是0了），但是如果Y0是1，也就是说Y是个负数的话，补码的运算方式就不能简单地照搬无符号数的移位-相加方式，需要在前面使用移位-相加且不计算Y的符号位的基础上，最后加上一个-X的补码，这也就是所谓矫正法

同时，这个结论也说明了一点，就是补码乘法和原码乘法的区别在于除数而不是被除数，对于被除数，无论是原码还是补码，处理方法是一样的

证明如下：

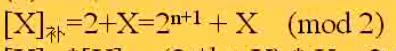
注意这里，由于mod运算，2的n+1次方和2是一样的

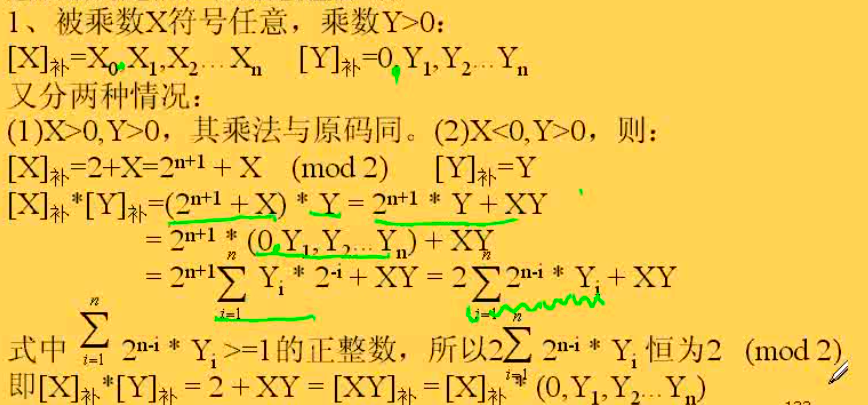
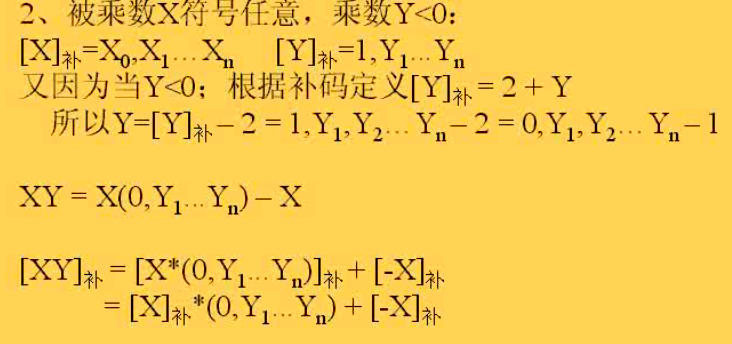
Booth算法

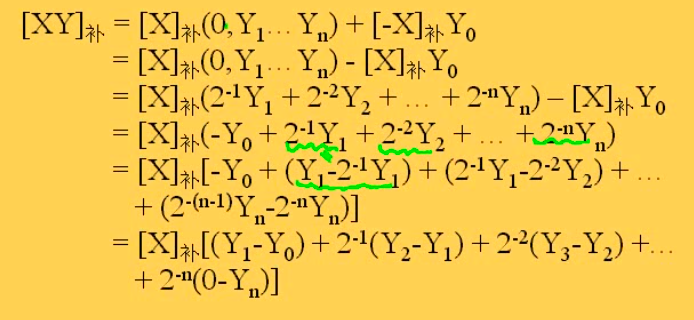
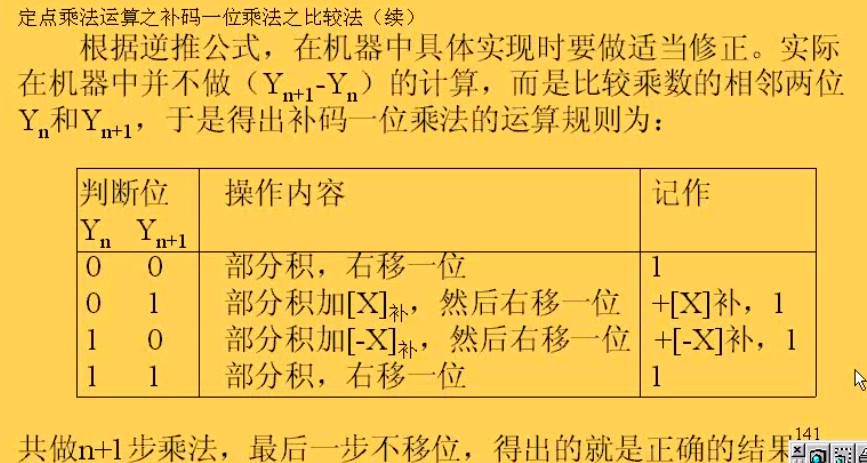
艹，我觉得这个比PolyU老师讲的明白多了

原码除法

原码除法的笔算示例:

如果左移一位的余数大于除数，就上商1

x0和y0之间进行的是异或操作

这里说的小数，它们的整数位都是0，也就是说它们都是小于1的

所以说，如果小数定点除法的小数部分除法结果大于1，直接报错就好，因为不符合约定了

• 恢复余数法

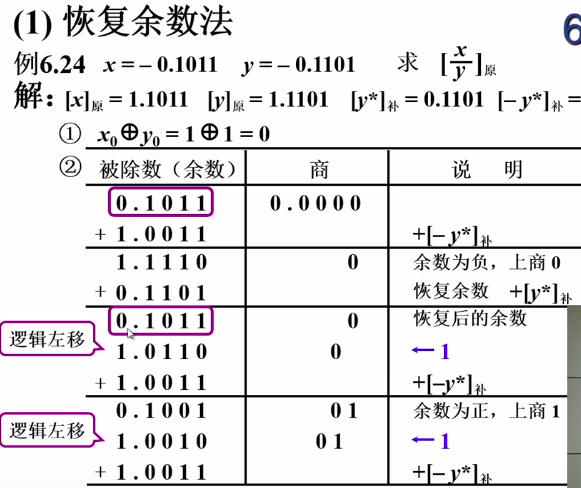
我们这里假设机器字长为5位

每次左移，就把商也同时左移，这样商从结果上来看就是从高到低进行的了，这样计算过程和笔算就完全一致了

• 不恢复余数法

先减去，再判断要上商0还是1，在分别做对应的操作，然后再判断

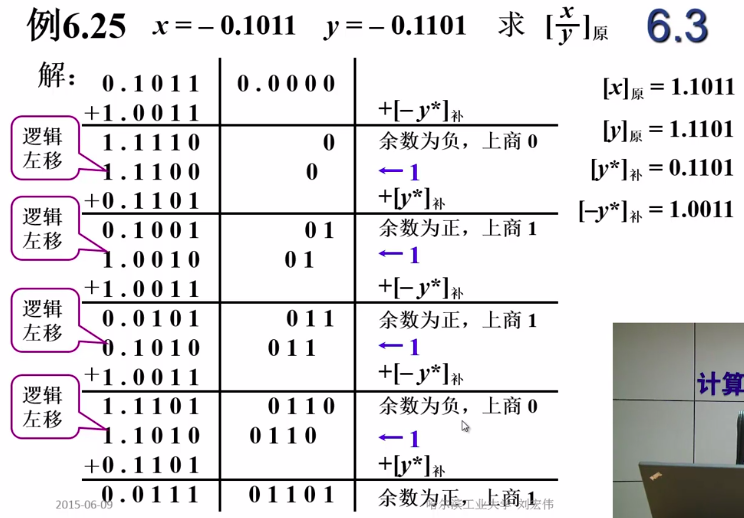
补码除法

补码的除法是在原码的不恢复余数的除法的基础上改进而成的

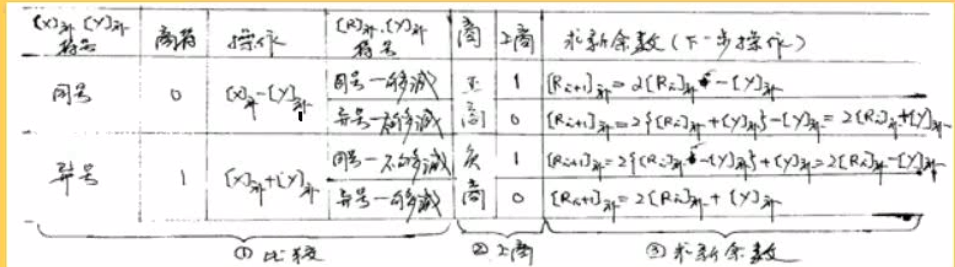
两个数要是同号的话每次就是减，否则就是加；如果商和除数是同号的话，说明不够减，此时上商要上反码，也就是不够减的时候反而上1、够减的时候反而上0；。注意这里用的是反码，所以最后需要矫正为补码

而同号和异号的操作其实是可以统一的，这一点要见上图的最后一栏，同号和异号的区别仅仅是在加和减上，他们的上商结果也是一致的：够减，也就是同号，上1；不够减，也就是异号，就上0：

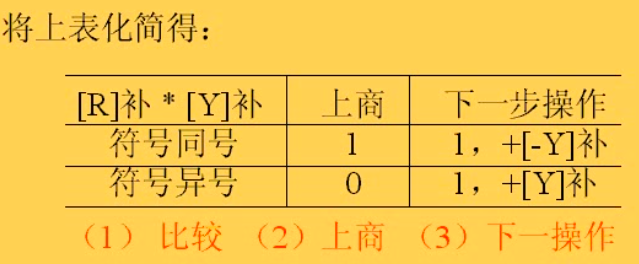
那么，如何确定商的符号呢？

商的符号为的计算要单独讨论，是因为这时是处于计算的开始阶段，是没有余数的，方法一可以看为是开始计算、创造一个原始的余数，而方法二是直接将被除数当成余数

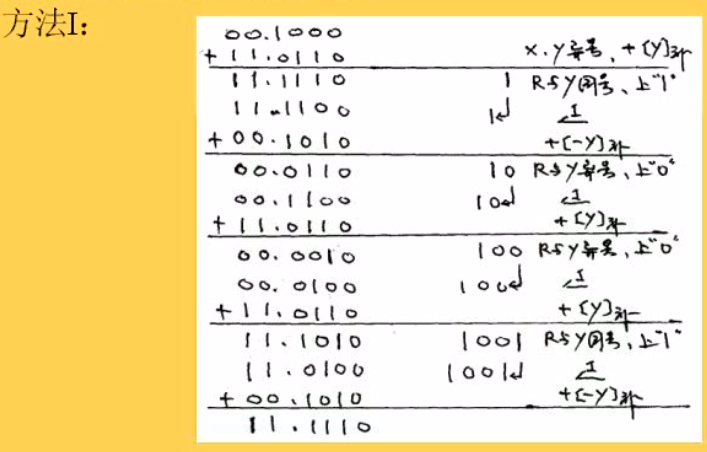
如果同号，减完了符号位就是0；异号的话加完了符号位就是1

注意，这里说的只涉及到符号位，所以使用方法二之后只需要将符号位取反就好了

符号位是反着的，所以加上1就可以使得符号位取反（可能有溢出，溢出的就被忽略了）

浮点数

使用原因

科学计算需要，只使用定点的话需要手动调整；并且定点数的表示范围小

r如果取2，那么尾数移动一位，阶码改变一位；r如果取4，那么尾数移动两位，阶码改变一位

规格化数：尾数的小数点后第一位为非0

注意阶码是用二进制数表示的

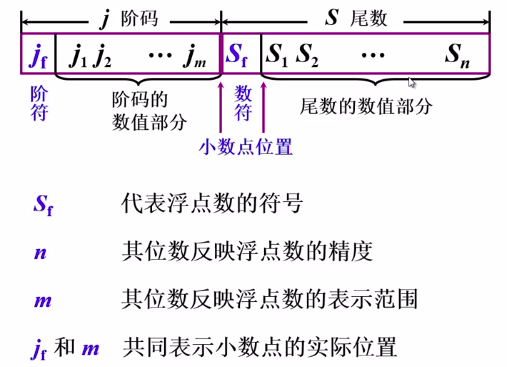
阶符：表示阶码的正负

注意这里说的不包括0，也就是尾数全为0、数符是0或者1(IEEE标准规定正负零是相等的）的情况

例如：

浮点数的规格化形式

原因是尽可能地保持浮点数的精度

注意这里讲的和PolyU课件上的规定不一样，那里的规定是，默认r=2，然后由于尾数最高位一定是1，所以这个1就不存了，所以它规格化的标准也不一样（这个其实是IEEE754的标准）：

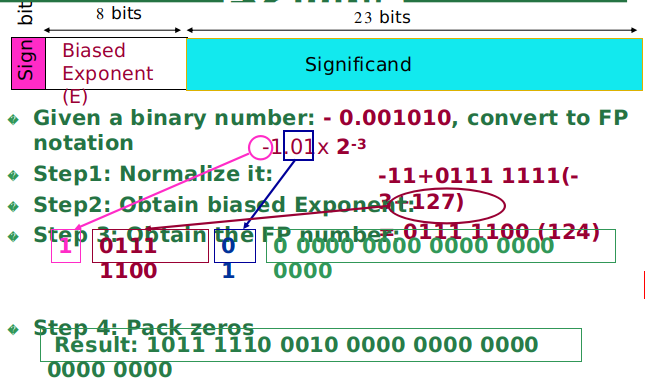
注意，对于阶码和尾数的正负表示是分开的

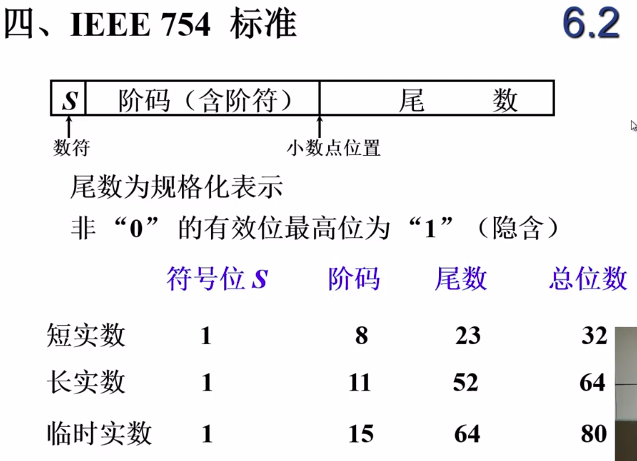
浮点运算

浮点运算的要求是，base必须是一样的

阶码不同的话，需要进行调整

对阶的过程中，数据位可能会出现数据丢失（因为数据位的最大长度是有限的），数据丢失最好是右侧丢失，所以最好采用低位向高位对齐的方式

例如：

规格化

但是是有特例的：

对于-1/2，需要单独对其进行规格化

-1没有源码，但是有补码

如何进行规格化

舍入

乘除法

看https://wenku.baidu.com/view/c1416473f46527d3240ce0b1.html

标签：表示,数制,运算,符号,补码,定点,小数,原码,计算机
来源： https://www.cnblogs.com/jiading/p/12240870.html