校招笔试题2019(京东):合唱队形
作者:互联网
校招笔试题2019(京东):合唱队形(标签:线性时间复杂度,贪心算法)
题目描述
合唱队的N名学生站成一排且从左到右编号为1到N,其中编号为i的学生身高为Hi。现在将这些学生分成若干组(同一组的学生编号连续),并让每组学生从左到右按身高从低到高进行排序,使得最后所有学生同样满足从左到右身高从低到高(中间位置可以等高),那么最多能将这些学生分成多少组?
输入
第一行包含一个整数N,1≤N≤10^5。
第二行包含N个空格隔开的整数H1到HN。1≤Hi≤10^9。
输出
输出能分成的最多组数。
样例输入
4
2 1 3 2
样例输出
2
解题思路
首先需要get到的点是:
若要成为一个组,需要满足:
1、组内的最小数要大于等于组前面(左边)所有数(即:最小数大于等于组前面最大数);
2、组内的最大数要小于等于组后面(右边)所有数(即:最大数小于等于组后面最小数)。
举个例子:3 1 2 (3 5 4) 6 序列中,(3 5 4)可以成为一个组,因为组内最小元素是3,其大于等于组前面最大数,即3;并且组内最大数为5,其小于等于组后面的最小数,即6。再举个反例,1 (3 2 5) 4 6序列中,(3 2 5)中最大的数为5,大于后面的4,所以(3 2 5)不能成为一个组。
有了以上分析,我们可以确定基本算法框架:使用贪心算法,因为需要分成的组最多,所以顺序遍历整个数组,只要能满足以上所述两个判断条件,即可成为一个组,并且遍历完成数组后,其组的数量是最多的。最初的思路可能需要O(n^2)的时间复杂度(即两个循环),首先是外层循环,其依次对数组中的每个元素进行遍历,内层循环再进行一次遍历以寻找组前面最大数和组后面最小数。但是这种算法明显做了重复的工作:内层循环每次遍历时,均会忘记上次寻找的过程,从第一个数重新找组外的极值,所以为了降低时间复杂度,提出以下线性时间复杂度算法。
此算法需要进行三次遍历,分别作用是:第一次遍历从左至右寻找某个位置前面的最小数,结果存放在left_max数组中;第二次遍历从右至左寻找某个位置后面的最大数,结果存放再right_min数组中;第三次遍历从左至右进行,使用贪心算法对队列进行分组。下文分别针对三次遍历,制作了三个动图,点击图片下方的开始按钮以播放图片,点击暂停按钮播放暂停以便查看具体某个步骤。
第一次遍历寻找某个位置前面的最小数:

第二次遍历寻找某个位置后面的最大数:
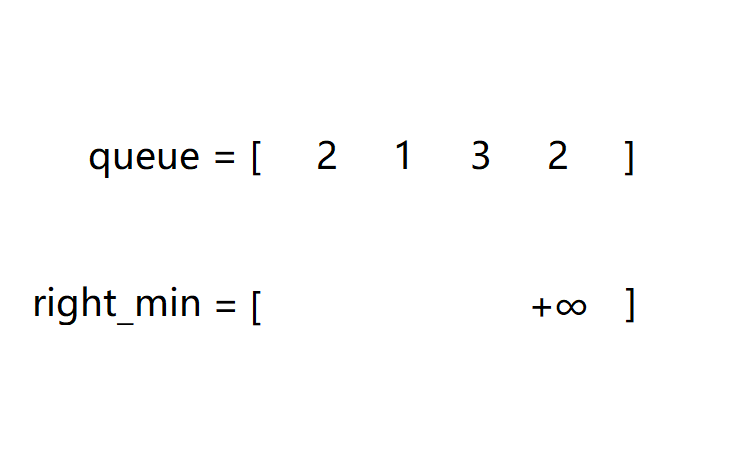
第三次遍历对队列进行分组,其中变量代表的意义如下图(不是动图)所示:

以下为算法分步骤动图:

当完成以上步骤后,分组数量可直接通过group_count取回。此题目没有要求具体的分组策略,若需要具体分组策略,可将int变量group_end改为数组形式存储所有的分组情况。
源代码
点击【执行】可在线查看程序执行结果。
<iframe frameborder="0" height="950" src="https://tool.lu/coderunner/embed/7Dw.html" width="650"></iframe>
标签:遍历,最大数,合唱队,最小,算法,2019,数组,分组,校招 来源: https://www.cnblogs.com/WongWai95/p/2019-JD-BI-SHI-TI-HE-CHANG-DUI-XING.html