[SCOI2012] 滑雪（最小树形图）

题意

给定一张图，每个节点有高度，一个点只能到达高度不大于它的其他点，求从1号节点出发所能到达的节点数（包括自己）以及这些节点的最小树形图（以1为根且可以到达其他点的树）的边权和

思路

从1出发能到达的点用一遍bfs即可求出，然后就相当于求剩下节点的最小树形图

如果所有边都是无向边，显然就是求最小生成树，而现在放到有向图里面，可以用朱刘算法，但是O(\(VE\))会超时，于是我们考虑一下这张图的特性

由于连边是由高度决定的，高度相等的连无向边，所以一定没有一个有向边组成的环。想一下为什么不能直接使用kruskal求最小生成树？因为这样的生成树可能会有从高度低的指向高度高的边（因为把有向边当成无向边了

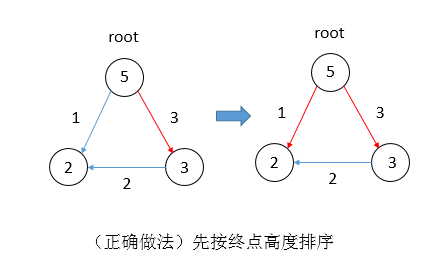
所以对kruskal的排序进行改进，以有向边终点高度为第一关键字从大到小排序，以边权为第二关键字从小到大排序，就可以直接使用kruskal了

为什么这样做是正确的？

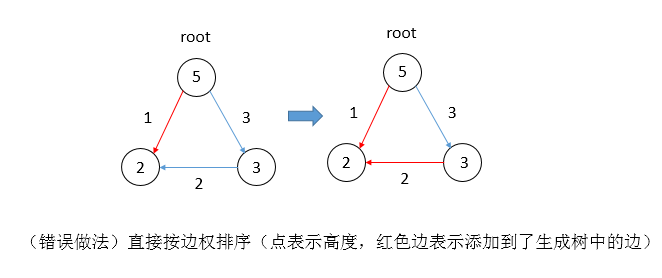
可以这样理解：既然一个点早晚要被加入这个生成树中，那么将高的点排在前面不会影响正确性；而且高的先加入就不会出现连反的情况了（矮的先加入的话可能到时候高的想要加入就必须要反向连边才行，如下图）

标签：排序,kruskal,高度,最小,树形图,节点,滑雪,SCOI2012
来源： https://www.cnblogs.com/Chtholly/p/11171086.html