LG3565 [POI2014]HOT-Hotels 题解
作者:互联网
P3565 [POI2014]HOT-Hotels
给定一棵树,在树上选 \(3\) 个点,要求两两距离相等,求方案数。
原题数据范围 \(n\leq 5000\),可做到线性,空间 \(62.5\text{MB}\)。
sub1
\(n\leq 5000\) 不用多说,直接枚举每一个点作为中点,统计这个点不同的三颗子树中点的选取方案数。定义 \(f_i\) 为先前找到的子树中深度为 \(i\) 的且在不同子树中的点对数,\(g_i\) 为先前找到的子树中深度为 \(i\) 的点的个数,\(bot_i\) 为当前子树中深度为 \(i\) 的点的个数。
每枚举一颗子树,得到转移
\[ans\gets f_i\times bot_i\\ f_i\gets g_i\times bot_i\\ g_i\gets bot_i \]sub2
不妨换个思路来想问题(指看题解后才懂)。
定义 \(f_{u,i}\) 为 \(u\) 的子树中距离 \(u\) 为 \(i\) 的节点数,\(g_{u,i}\) 为 \(u\) 的子树中的一对的 \(lca\) 到 \(u\) 节点的距离是 \(d-i\) 的方案数(也就是说这对点到 \(lca\) 的距离是 \(d\))。
如图(是自己画的呢)
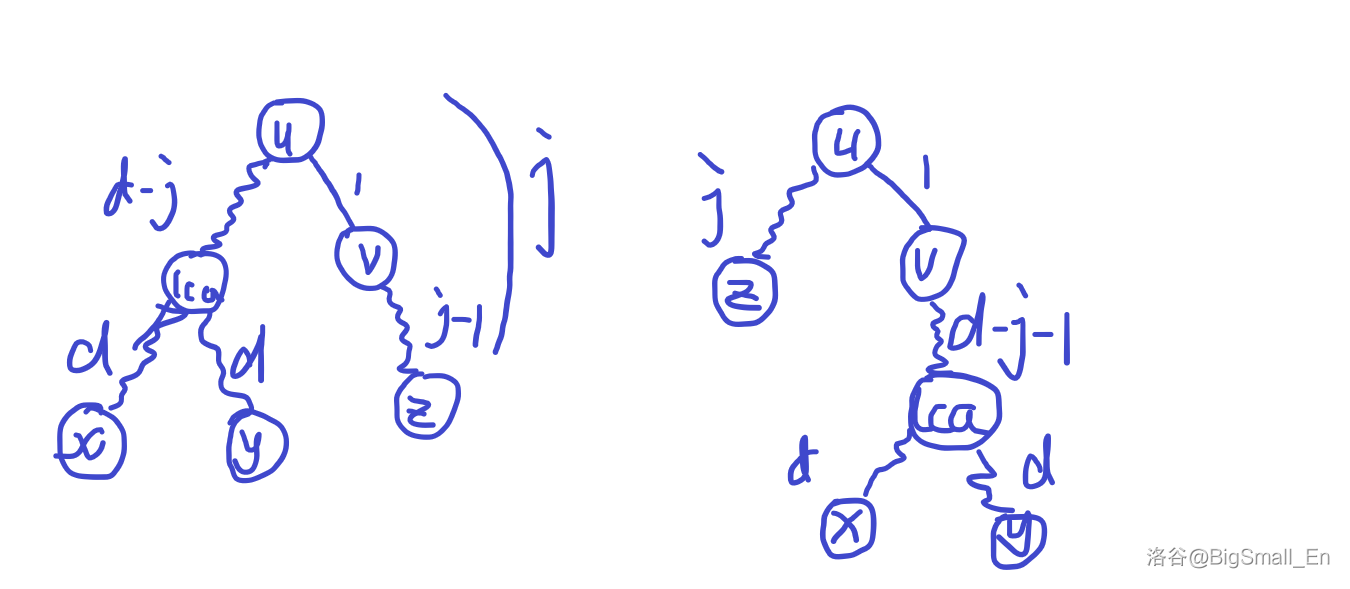
根据这题的要求 \(dis(x,z)=dis(x,y)=2\times d\),可以得到 \(dis(v,z)=2\times d-(d-j)-d-1=j-1\)。
如果现在加入子树 \(v\) 可以计算出答案:
\[ans\gets f_{v,j-1}\times g_{u,j}+f_{u,j}\times g_{v,j+1}+g_{u,0} \]同时更新信息
\[g_{u,i}\gets f_{u,i}\times f_{v,i-1}+g_{v,i+1}\\ f_{u,i}\gets f_{v,i-1} \]每次转移的复杂度是 \(v\) 子树的最大深度,即 \(maxdep_v-dep_u+1\)。
至此我们可以 \(O(n^2)\) 解决这个问题。
sub3
如果 \(u\) 只有一个儿子 \(v\),可以发现 \(f_{u,i}=f_{v,i-1},g_{u,i}=g_{v,i+1}\)。这显然可以直接用指针来继承 \(dp\) 数组。
我们可以使用长链剖分优化这个 \(dp\),长(重)儿子直接指针转移,轻儿子暴力合并即可。因为单次转移的复杂度是树的一条链的长度,这些链不重叠,所以时间复杂度 \(O(n)\)。
代码实现
指针实现的时候为
f[son[u]]=f[u]+1;
g[son[u]]=g[u]-1;
容易 \(g\) 数组儿子节点的初始位置甚至会往前走,所以要 \(g\) 数组的 \(temp\) 数组要开双倍空间,同时预留空间的时候前方也必须预留。
此外所有的题解的转移的 \(u,v\) 和我是相反的,尽管这两者本质相同,我用我的图推出来的转移就是这样的,我也不知道题解是怎么推得如此一致,还是说。。。
const int N=1000006;
vector<int>edge[N];
int n,fat[N],son[N],len[N];//len记录子树内最深的点到这颗子树的根的距离
ll *f[N],tf[N],*pf=tf+1,*g[N],tg[N<<1],*pg=tg+1,ans;
void dfs(int u,int f){
fat[u]=f;
for(auto v:edge[u]){
if(v==f)continue;
dfs(v,u);
len[u]=max(len[u],len[v]);
if(len[v]>len[son[u]])son[u]=v;
}++len[u];
}
inline void space(int u){
f[u]=pf,pf+=len[u];
pg+=len[u];g[u]=pg,pg+=len[u];//g数组的指针会往前走,所以需要在前面预留空间。
}
void dfsp(int u){
if(son[u]){f[son[u]]=f[u]+1,g[son[u]]=g[u]-1;dfsp(son[u]);}
f[u][0]=1;ans+=g[u][0];
for(auto v:edge[u]){
if(v==fat[u]||v==son[u])continue;
space(v);dfsp(v);
for(int i=0;i<=len[v];++i){
if(i)ans+=f[v][i-1]*g[u][i];
ans+=g[v][i+1]*f[u][i];
}
for(int i=0;i<=len[v];++i){
if(i)g[u][i]+=f[u][i]*f[v][i-1];
g[u][i]+=g[v][i+1];
if(i)f[u][i]+=f[v][i-1];
}
}
}
int main(){
n=read();
for(int i=1;i<n;++i){
int u=read(),v=read();
edge[u].push_back(v);
edge[v].push_back(u);
}
dfs(1,0);
space(1);dfsp(1);
printf("%lld\n",ans);
return 0;
}
// 152ms / 35.19MB / 1.36KB C++14 (GCC 9) O2
//如何评价你谷所有题解的dp转移方向都是一样的。。。
标签:子树,int,题解,POI2014,times,HOT,len,son,gets 来源: https://www.cnblogs.com/BigSmall-En/p/16643683.html