卡特兰数学习笔记
作者:互联网
卡特兰数(Catalan 数)学习笔记
一、引入
问题 1
由 \(n\) 个 \(+1\) 和 \(n\) 个 \(-1\) 组成的 \(2n\) 项序列 \(a_1,a_2,\cdots,a_{2n}\),求有多少种方案满足其部分和 \(a_1+a_2+\cdots+a_k \ge 0\ (k=1,2,\cdots,2n)\)。
分析
设满足条件的方案数(即答案)为 \(C_n\),不满足条件的方案数为 \(U_n\)。
由 \(n\) 个 \(+1\) 和 \(n\) 个 \(-1\) 组成的序列总数为 \(\dfrac{(2n)!}{n!n!}=\dbinom{2n}{n}\)
那么 \(C_n+U_n=\dbinom{2n}{n}\)
我们只要求出 \(U_n\),就可以得到 \(C_n\)。
因为不满足条件,所以一定存在第一个 \(k\),使得 \(a_1+a_2+\cdots+a_k<0\)。
因为 \(k\) 是第一个,所以 \(a_1+a_2+\cdots+a_{k-1}=0\),且 \(a_k=-1\)。
同时,\(k\) 为奇整数。
我们将前 \(k\) 项的符号取反,剩下的不变,就可以得到一个由 \(n+1\) 个 \(+1\) 和 \(n-1\) 个 \(-1\) 组成的序列,而这个序列和前面不满足条件的序列一一对应(考虑第一个 \(+1\) 个数超过 \(-1\) 的位置,将这个位置及其前面符号取反,就可以得到一个不满足条件的序列)。
那么 \(U_n\) 等于由 \(n+1\) 个 \(+1\) 和 \(n-1\) 个 \(-1\) 组成的序列的个数,即 \(\dfrac{(2n)!}{(n+1)!(n-1)!}=\dbinom{2n}{n+1}\)。
所以 \(C_n=\dbinom{2n}{n}-\dbinom{2n}{n+1}=\dfrac{1}{n+1}\dbinom{2n}{n}\)。
即为第 \(n\) 个卡特兰数。
扩展
若改为 \(n\) 个 \(+1\),\(m\) 个 \(-1\),且 \(n\ge m\),那么有多少种?
分析
同样设满足条件方案数为 \(A_n\),不满足的为 \(U_n\)。
那么 \(A_n+U_n=\dbinom{n+m}{n}\)。
\(U_n=\dbinom{n+m}{n+1}\),所以 \(A_n=\dbinom{n+m}{n}-\dbinom{n+m}{n+1}\)。
问题 2
求以下递推关系的解:
\(C_0=1\)
\(C_n=C_0C_{n-1}+C_1C_{n-2}+\cdots+C_{n-1}C_0=\sum\limits_{k=0}^{n-1}C_kC_{n-k-1}\)
分析
设 \(g(x)=C_0+C_1x+C_2x^2+\cdots+C_nx^n+\cdots\) 为数列 \(C_0,C_1,\cdots,C_n\) 的生成函数。
\[(g(x))^2=C_0C_0+(C_0C_1+C_1C_0)x+(C_0C_2+C_1C_1+C_2C_0)x^2+\cdots+(C_0C_n+C_1C_{n-1}+\cdots+C_nC_0)x^n \\ =\sum\limits_{i=0}^{\infty}C_{i+1}x^i \]故
\[x(g(x))^2=\sum\limits_{i=0}^\infty C_ix^i-C_0=g(x)-C_0 \\ x(g(x))^2-g(x)+1=0 \]解得
\[g(x)=\dfrac{1\pm \sqrt{1-4x}}{2x} \]又
\[\lim\limits_{x\to0^+}g(x)=C_0=1 \\ \lim\limits_{x\to0^+}g(x)=\lim\limits_{x\to0^+}\dfrac{1\pm \sqrt{1-4x}}{2x}=\lim\limits_{x\to 0^+}\dfrac{2}{1\mp\sqrt{1-4x}} \]故 \(g(x)=\dfrac{1-\sqrt{1-4x}}{2x}\)
由牛顿二项式定理,
\[(1+z)^{\frac{1}{2}}=\sum\limits_{k=0}^{\infty}\dbinom{\frac{1}{2}}{k}x^k \]对于 \(k>0\),
\[\dbinom{\frac{1}{2}}{k}=\dfrac{\frac{1}{2}(\frac{1}{2}-1)\cdots(\frac{1}{2}-k+1)}{k!} \\ =\dfrac{(-1)^{k-1}}{2^k}\dfrac{1\times 3\times 5\times\cdots\times(2k-3)}{k!} \\ =\dfrac{(-1)^{k-1}}{2^k}\dfrac{1\times 2\times 3\times 4\times\cdots\times(2k-3)\times(2k-2)}{2\times 4\times\cdots\times(2k-2)\times (k!)} \\ =\dfrac{(-1)^{k-1}}{k\times 2^{2k-1}}\dfrac{(2k-2)}{((k-1)!)^2} \\ =\dfrac{(-1)^{k-1}}{k\times 2^{2k-1}}\dbinom{2k-2}{k-1} \]以 \(-4x\) 代 \(z\),可得
\[\sqrt{1-4x}=1+\sum\limits_{k=1}^{\infty}\dfrac{(-1)^{k-1}}{k*2^{2k-1}}\binom{2k-2}{k-1}(-1)^k4^kx^k \\ =1-2\sum\limits_{k=1}^{\infty}\dfrac{1}{k}\binom{2k-2}{k-1}x^k \]故
\[g(x)=\dfrac{1}{2x}(1-(1-2\sum\limits_{k=1}^{\infty}\dfrac{1}{k}\binom{2k-2}{k-1}x^k)) \\ =\dfrac{1}{2x}2\sum\limits_{k=1}^{\infty}\dfrac{1}{k}\binom{2k-2}{k-1}x^k \\ =\sum\limits_{k=0}^{\infty}\dfrac{1}{k+1}\dbinom{2k}{k}x^k \]即 \(C_n=\dfrac{1}{n+1}\dbinom{2n}{n}\)
即第 \(n\) 个卡特兰数。
二、应用
例 1
问题
有 \(2n\) 个人排列进入剧场,票价 \(5\) 角。其中 \(n\) 个人有 \(5\) 角硬币,另外 \(n\) 个人有一元硬币。初始售票处无零钱。问有多少种排列方法使得每个有一元硬币的人买票时,都有 \(5\) 角找零?
分析
有 \(5\) 角找零的条件为:在任一位置,有 \(5\) 角硬币的人总数大于等于有一元硬币的人个数。
将有 \(5\) 角硬币的人看作 \(+1\),有一元硬币的人看作 \(-1\),那么就转化为引入中的问题 1。答案为第 \(n\) 个卡特兰数。
例 2
问题
对于一个 \(n\times n\) 的正方形网格,从左下角到右上角,每次只能向右或向上走一格,且不能越过对角线,问有多少种走法。
分析
考虑将向右记为 \(+1\),向上记为 \(-1\),那么合法路径的数目就等于满足 \(\sum\limits_{i=1}^{k}a_i \ge 0\ ,k=1,2,\cdots,2n\),即引入中问题 1。
所以答案即为第 \(n\) 个卡特兰数。
例 3
问题
计算包含 \(n\) 个左括号和 \(n\) 个右括号的合法括号序列种数。
合法括号序列定义:
空串为合法序列。
若 A 为合法序列,那么 (A) 为合法序列。
若 A,B 均为合法序列,那么 AB 为合法序列。
分析
显然在任何位置,左括号的个数一定大于等于右括号的个数。
考虑将左括号看作 \(+1\),右括号看作 \(-1\),那么又转化成了引入中的问题 1,答案是第 \(n\) 个卡特兰数。
例 4
问题
计算 \(n\) 个数合法的出栈序列。
分析
法一:将进栈看作 \(+1\),出栈看作 \(-1\),那么就转化成了引入中的问题 1。
法二:
设答案为 \(c_n\)。
显然 \(c_0=1\)。
我们考虑 \(c_n\) 怎么得来。
令最后一个出栈的数为 \(k\)。
那么在 \(k\) 入栈之前,\(1,2,\cdots,k-1\) 共 \(k-1\) 个数已经入栈并出栈了,方案数为 \(c_{k-1}\)。
在 \(k\) 入栈之后,\(k+1,\cdots,n-1,n\) 共 \(n-k\) 个数会入栈并出栈,方案数为 \(c_{n-k}\)。
故总方案数为 \(\sum\limits_{k=1}^n c_{k-1}c_{n-k}=\sum\limits_{k=0}^{n-1}c_kc_{n-k-1}=C_n\)。
转化成引入中的问题 2。
例 5
问题
求将 \(n+2\) 条边的凸多边形用不相交的对角线分割成三角形区域的方案数。
分析
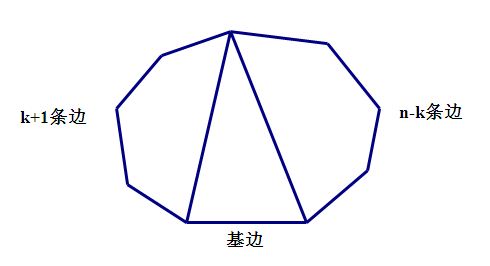
如图,我们选定这个多边形的一条边作为基边,那么在每一种划分中这条基边都是一个三角形区域的边,且这个三角形区域将整个多边形分成了三部分:这个三角形区域,一个含有 \(k+1+1=k+2\) 条边的多边形区域,还有一个含有 \(n+2-k-1-1+1=n-k+1\) 条边的区域。
设含 \(n+2\) 条边的方案数为 \(c_n\)。
那么由分析可知,\(c_n=\sum\limits_{k=0}^{n-1} c_kc_{n-k-1}=C_n\)。
转化为引入中的问题 2。
例 6
问题
求含有 \(n\) 个节点的二叉树的个数。
分析
首先固定一个根节点,左子树有 \(k\) 个节点,那么右子树有 \(n-k-1\) 个节点。
设答案为 \(c_n\),那么 \(c_n=\sum\limits_{k=0}^{n-1}c_kc_{n-k-1}=C_n\)。
转化为引入中的问题 2。
三、公式
- 计算式:\(C_n=\dfrac{1}{n+1}\dbinom{2n}{n}\)。
- 递推式 1:\(C_0=1,C_n=\sum\limits_{k=0}^{n-1}C_kC_{n-k-1}\)
- 递推式 2:\(C_0=1,C_n=\dfrac{4n-2}{n+1}C_n-1\)
- 增长趋势:\(C_n\thicksim\dfrac{4^n}{n^\frac{3}{2}\sqrt{\pi}}\)
标签:dbinom,limits,dfrac,笔记,times,学习,cdots,2n,卡特兰 来源: https://www.cnblogs.com/sysong2006/p/16634272.html