P5021 [NOIP2018 提高组] 赛道修建 思路简记

发现答案具有单调性，尝试一下二分答案能不能做

二分答案 \(t\) 后，问题的关键就变成最多能找到多少条长度大于等于 \(t\) 的赛道

我们先假设整棵树以 \(1\) 为根

把样例的图放出来：

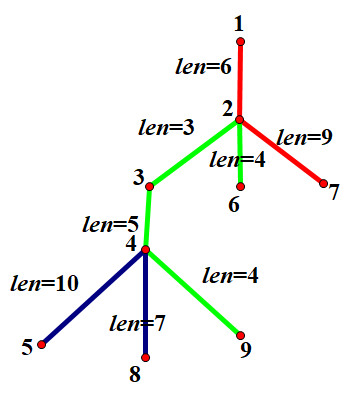
我们可以发现一个性质：

如果一个链，它经过了结点 \(i\) 的父结点，同时包含了 \(i\) 到子结点的某条边，那么它只能包含 \(i\) 到所有子结点的边当中的一条。

也就是说对于任意一个点 \(i\) (其父亲为 \(fa\)) 以及其子树内的节点 \(j,k\)，对于链 \(j\to i\)，我们只用考虑 \(3\) 种情况

• 不用这条链

• 用 \(j\to i\to k\) 这条链

• 用 \(j\to i\to fa\) 这条链 (注意 \(i\to fa\) 只能用一次)

那么我们贪心地考虑的就是：先按照第二种情况尽量将 \(i\) 子树各种链合并，然后在把剩下链中长度最大的链和 \(i\to fa\) 合并，传给 \(fa\)。

那么我们就可以采用双指针的方式贪心配对，让每一条链匹配到可行的且长度最小的链

这里我用的是 \(multiset\) \(+\) 二分实现

#include<bits/stdc++.h>
using namespace std;

const int N=5e4+5;
const int inf=1e9;

struct node{
	int x,v;
};

int n,m;
vector <node> G[N];

inline node dfs(int x,int fa,int t){
	multiset <int> s;
	node now={0,0};
	for(auto y:G[x]){
		if(y.x==fa) continue;
        node tmp=dfs(y.x,x,t);
		int val=tmp.x+y.v;
        now.v+=tmp.v;
		if(val>=t) ++now.v;
		else s.insert(val);
	}
	while(!s.empty()){
		int nowv=*s.begin();
		if(s.size()==1){
			now.x=max(now.x,nowv);
			break;
		}
		auto tmp=s.lower_bound(t-nowv);
		if(tmp==s.begin()&&s.count(*tmp)==1) ++tmp;
		if(tmp!=s.end()){
			++now.v;
			s.erase(s.find(*tmp));
		}
		else now.x=max(now.x,nowv);
		s.erase(s.find(*s.begin()));
	}
	return now;
}

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1,x,y,z;i<n;++i){
		cin>>x>>y>>z;
		G[x].push_back({y,z});
		G[y].push_back({x,z});
	}
	int l=0,r=inf;
	while(l<r-1){
		int mid=l+r>>1;
		if(dfs(1,0,mid).v>=m) l=mid;
		else r=mid;
	}
	cout<<l<<endl;
}

标签：赛道,tmp,node,int,NOIP2018,fa,P5021,nowv,now
来源： https://www.cnblogs.com/into-qwq/p/16621304.html