图的遍历(深搜和宽搜)
作者:互联网
深度优先搜索 (Depth First Search)
深度优先搜索也叫深度优先遍历,简称DFS或者深搜。
是基于栈的搜索算法,其过程,是对每一个可能的分支路径深入到不能再深入为止,而且每个结点只能访问一次。
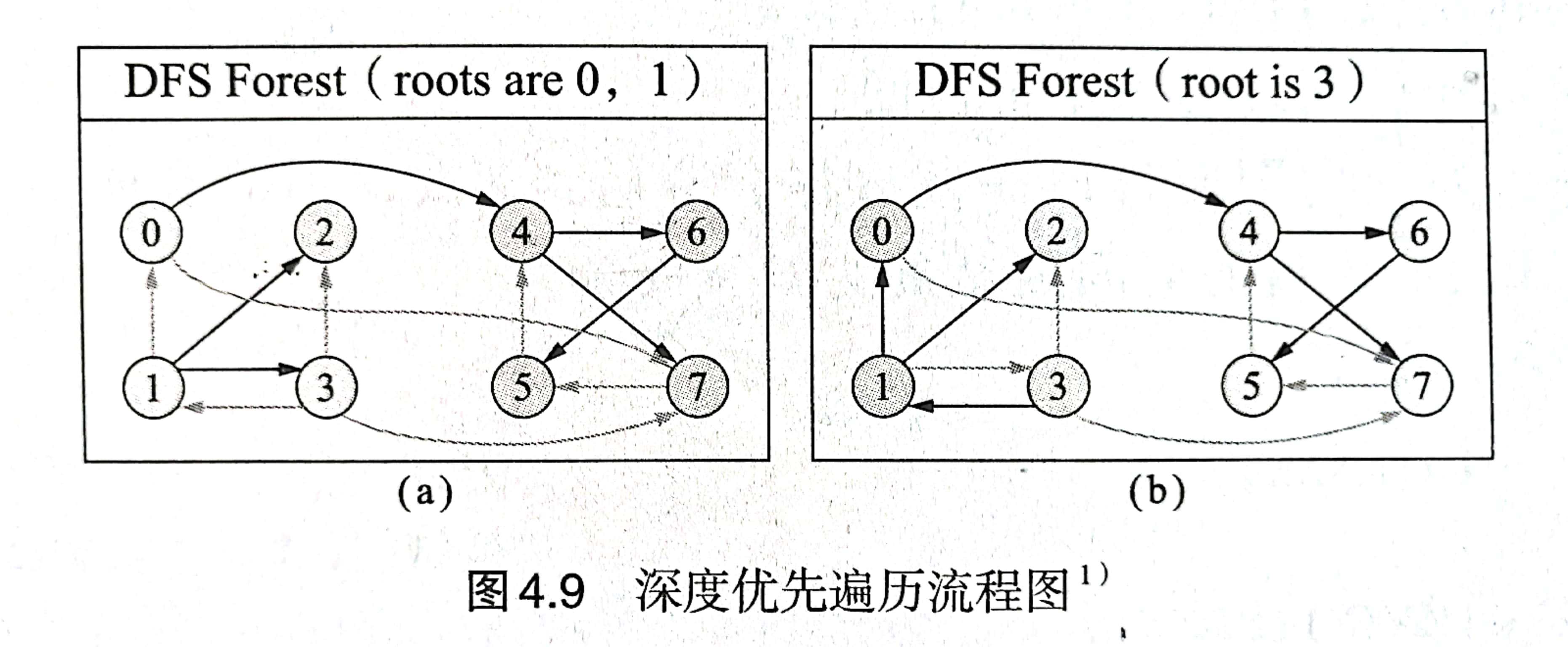
图解:
| 当前访问 | 入栈结点 | 出栈结点 | 栈内结点 | 说明 |
|---|---|---|---|---|
| 0 | 0 | 0 | 以0为根开始遍历 | |
| 4 | 4 | 0,4 | ||
| 6 | 6 | 0,4,6 | ||
| 5 | 5 | 0,4,6,5 | ||
| 5 | 0,4,6 | 5的儿子全部遍历,弹栈 | ||
| 6 | 0,4 | 6的儿子全部遍历,弹栈 | ||
| 7 | 7 | 0,4,7 | ||
| 7 | 0,4 | 7遍历完毕,弹栈 | ||
| 4 | 0 | 4遍历完毕,弹栈 | ||
| 0 | 栈空 | 0遍历完毕,弹栈 | ||
| 1 | 1 | 1 | 以1为根开始遍历 | |
| 2 | 2 | 1,2 | ||
| 2 | 1 | 2遍历完毕,弹栈 | ||
| 3 | 3 | 1,3 | ||
| 3 | 1 | 3遍历完毕,弹栈 | ||
| 1 | 栈空 | 1遍历完毕,弹栈 |
邻接表:
void DFS(int u)
{
visited[u]=1;//printf("%d ",u);//用于验证的输出
for(int i=adj[u];i;i=e[i].nxt)//深度优先的遍历
{
int v=e[i].to;
if(visited[v] == 1) continue;
DFS(v);//用递归来形成栈
}
}
int main()
{
int n,m;scanf("%d%d",&n,&m);//n是结点数,m是边数
for(int i=1;i<=m;++i)
{
int u,v; scanf("%d%d",&u,&v);
addedge(u,v);//有向图
}
for(int i=0;i<n;++i){
if(visited[i] == 0)
DFS(i);
//printf("\n");//用于验证的输出
}
return 0;
}
邻接矩阵:
bool visited[MAXN];
bool G[MAXN][MAXN];
void DFS(int u)
{
vis[u]=1;
for(int i=1;i<=n;++i)
{
if(G[u][i] == 0) continue;//如果不连接
if(visited[i]==1)continue;//如果已经访问
DFS(i);
}
}
上面图例的数据:
/*上图数据
7 13
1 0
1 3
3 1
1 2
3 2
0 4
5 4
6 5
4 7
7 5
3 7
0 7
4 6
*/
宽度优先搜索(Breadth First Search)
宽度优先搜索也叫宽度优先遍历,或是广度优先遍历,简称BFS或者宽搜。
是基于队列的搜索算法,其过程,是将一个点所有邻接点都遍历完再往下搜索。
还是上面那张图:以0,1为根的宽搜序列为:0,4,7,6,5,1,2,3。
| 当前访问 | 入队列 | 出队列 | 队列内结点 | 说明 |
|---|---|---|---|---|
| 0 | 0 | 0 | 以0为根开始遍历 | |
| 0 | 空 | 0出队列 | ||
| 4 | 4 | 4 | 从4开始遍历0的儿子 | |
| 7 | 7 | 4,7 | ||
| 4 | 7 | 4出队列 | ||
| 6 | 6 | 7,6 | 从6开始遍历4的儿子 | |
| 7 | 6 | 7出队列 | ||
| 5 | 5 | 6,5 | 从5开始遍历7的儿子 | |
| 6 | 5 | 6出队列 | ||
| 5 | 空 | 5出队列 | ||
| 1 | 1 | 1 | 以1为根开始遍历 | |
| 1 | 空 | 1出队列 | ||
| 2 | 2 | 2 | 从2开始遍历1的儿子 | |
| 3 | 3 | 2,3 | ||
| 2 | 3 | 2出队列 | ||
| 3 | 空 | 3出队列 |
邻接表:
void BFS(int u)//用STL的队列
{
q.push(u); visited[u]=1;//visited表示已访问
while(!q.empty())
{
int u=q.front();q.pop();
for(int i=adj[u];i;i=e[i].nxt)
{
int v=e[i].to;
if(visited[v] == 1) continue;
visited[v]=1;
q.push(v);
}
}
}
对比
深度优先搜索用栈来实现,整个过程可以想象成一个倒立的树形:
1、把根节点压入栈中。
2、每次从栈中弹出一个元素,搜索所有在它下一级的元素,把这些元素压入栈中。并把这个元素记为它下一级元素的前驱。
3、找到所要找的元素时结束程序。
4、如果遍历整个树还没有找到,结束程序。
广度优先搜索使用队列(queue)来实现,整个过程也可以看做一个倒立的树形:
1、把根节点放到队列的末尾。
2、每次从队列的头部取出一个元素,查看这个元素所有的下一级元素,把它们放到队列的末尾。并把这个元素记为它下一级元素的前驱。
3、找到所要找的元素时结束程序。
4、如果遍历整个树还没有找到,结束程序。
标签:弹栈,遍历,队列,元素,int,visited 来源: https://www.cnblogs.com/cyl-oi-miracle/p/16537597.html