U231111 最终的归宿 题解

观察到题目中 \((x, y) \oplus (y, z) = (z, x)\) 的特殊二元组生成方式，我们很容易联想到三元环，于是思考到能不能用图论解决这个问题。

具体在这个题目上，也就是给定了一个有向图，无重边有自环，一旦有 \(x \to y, y\to z\)，我们能迭代出一条 \(z \to x\) 的边，问最后总图有多少边。

根据题意，这个图不一定联通，但明显地，对于整个图而言，所有的弱联通块之间可以独立处理答案，最终的答案是这些弱联通块答案的总和。所以我们接下来处理的对象都是单个弱联通块。

（弱联通块的意思就是：该块中所有边不考虑方向，那么这个块是联通的）

我们考虑最简单的情况：一条链，并且一定以 \(1\) 开头。

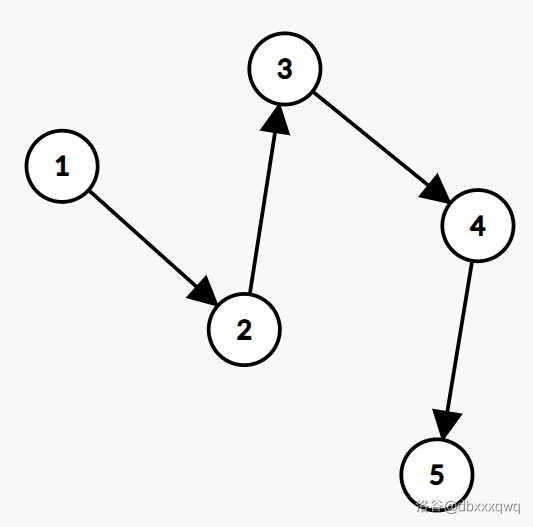
我们发现可以至少迭代出这样三条边：\(3 \to 1, 4 \to 2, 5 \to 3\).

然后发现：好像类似于一个大小为 \(3\) 的循环。于是想到一个方案：对节点染色，色彩也按照一个大小为 \(3\) 的周期循环。具体用公式表示（为方便，我们将节点 \(i\) 的颜色表示为 \(c_i\)）：

如果存在一条边 \(u \to v\)，我们的染色要使

\[c_v=\begin{cases}c_u + 1& c_u \in \{1, 2\}\\1 & c_u = 3\end{cases} \]

聪明的小伙伴发现这种染色方案可能无法实现。具体来说，染色的结果有三种情况：

• 染色一切顺利，三个颜色染全；
• 染色一切顺利，三个颜色没有染全；
• 染色时出现矛盾（染色失败）。

以此图为例，染色情况为，\(1\) 染成 \(1\)，\(2\) 染成 \(2\)，\(3\) 染成 \(3\)，\(4\) 染成 \(1\)，\(5\) 染成 \(2\)。属于第一种情况，染色成功并且三个色彩都有。

这样一来，\(3 \to 1\) 对应颜色 \(3 \to 1\)，\(4 \to 2\) 对应颜色 \(1 \to 2\)，\(5 \to 3\) 对应颜色 \(2 \to 3\)。

于是嘴一个做法：如果存在两个点 \(u, v\)，使得 \(c_u = 1, c_v = 2\) 或者 \(c_u = 2, c_v = 3\) 或者 \(c_u = 3, c_v = 1\)，那么就连一条 \(u \to v\) 的边，接下来为了叙述方便，我们将这种边叫做正边。

哦，这下我们还发现，原来刚刚我们落了一条边没连：\(1 \to 5\)（形成的三元环为 \(3 \to 1 \to 5 \to 3\)）。总共边数为 \(8\)。

但刚刚的情况太简单，我们能否换成一般的图呢？

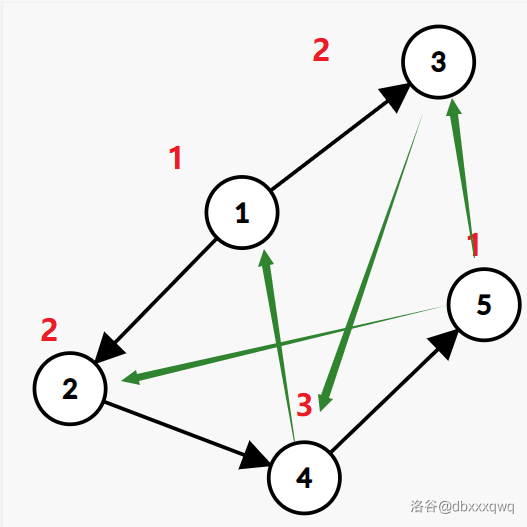
如图中的黑边就是原边，我们按照黑边将节点染色（图中的红字），然后再连接出所有正边（图中的绿边），既可以形成上方这个图。手动按照题目模拟一下，发现满足题意。

严格证明这个命题：染色结果为第一种情况时，所有的正边的集合就是答案。

此时一定存在 \(x, y, z\) 使得边 \(x \to y\) 和 \(y \to z\) 存在（原因：三种颜色染全），并且 \(c_x, c_y, c_z\) 要么分别等于 \(1, 2, 3\)，要么分别等于 \(2, 3, 1\)，要么分别等于 \(3, 1, 2\)。根据对称性我们只假定第一种情况，即 \(c_x = 1, c_y = 2, c_z = 3\)。首先明显地，我们能迭代一条 \(z \to x\) 的边，\(x, y, z\) 形成三元环。明显此时所有正边就是答案。假设目前讨论的总点数为 \(n\)（注意和题目中 \(n\) 的含义不同）。现在我们就可以说：\(n = 3\) 时，命题成立。

接下来来几个命题：

命题：如果存在 \(u \to v\) 且 \(u \to w\)，那么有 \(c_v = c_w\)。

命题：如果存在 \(v \to u\) 且 \(w \to u\)，那么有 \(c_v = c_w\)。

命题：不可能存在 \(u \to v\) 且 \(v \to u\)。

证明：第一个命题看一下怎么染色的就明白了……

第二个命题，反证法，假设 \(c_v \neq c_w\)，那么立刻推导出来 \(c_u \neq c_u\)，寄。

第三个命题同样也反证法，也能推出来 \(c_u \neq c_u\)，此处不过多说明。

命题：不存在一个节点 \(u\) 使得 \(u \to x\) 且 \(u \to y\)。

命题：不存在一个节点 \(u\) 使得 \(x \to u\) 且 \(y \to u\)。

证明：注意这里 \(x, y, z\) 是前面定义的那三个点哦。两个都是反证法，命题成立可以推出来 \(c_x = c_y\)，和题设矛盾。同时这两个命题可以对称，也就是 \(x, y\) 可以替换为 \(x, y, z\) 中的任何一对（比如 \(y, z\)）。

命题：初始的图中所有边都是正边。

证明：这是显然的，因为颜色本就是根据图中的边染的。

命题：任何一次迭代新生成的边都是正边。

证明：假设边集 \(E\) （对应原题的集合 \(S\)）中的边都是正边，按照迭代规则生成的边也应该是正边。初始时边集 \(E\) 中是正边，那么第一次迭代后加入边集 \(E\) 的是正边，因此满足边集 \(E\) 中的边永远是正边，因此满足任何一次迭代新生成的边都是正边。

这个命题比较有价值意义，因为它直接证明了原命题的必要性，现在只需要证明充分性，也就是所有正边都是迭代的答案，或者说迭代的答案一定包含了所有正边。

然后开始真正的证明：

假如有一个点 \(u\)，满足 \(u \to x\) 存在，那么就会迭代出 \(u \to x \to y \to u\) 这样一个三元环；对应地，假如满足 \(x \to u\) 存在，那么就会迭代出 \(x \to u \to z \to x\) 这样一个三元环。同理根据对称性可知：假如一个点 \(u\) 和 \(x ,y, z\) 中的任意一个点相邻（中间有一条边，不管方向），那么迭代一次后 \(u\) 会和 \(x, y, z\) 中的恰好两个点相邻，并且有且只有一条从 \(u\) 出发连向 \(x, y, z\) 中某一点的边，有且只有一条从 \(x, y, z\) 中某一点连向 \(u\) 的边。

说的有点复杂啊，其实就是这样一张图：

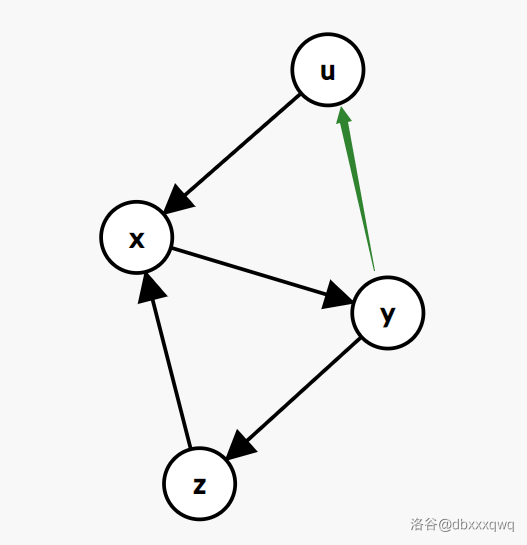
这里是 \(u \to x\) 的情况；明显地 \(u \to y\)，\(u \to z\) 这两种情况同理；\(y \to u\) 也是上面这种图的连边，只不过现在是 \(y \to u\) 黑色，\(u \to x\) 绿色了。\(x \to u\) 和 \(z \to u\) 同理。

此时，明显 \(x, y, z\) 内部所有的正边已经连接，而 \(u\) 与 \(x, y, z\) 迭代形成的两个正边也已经全部连接。同时注意到，\(u\) 和 \(x, y, z\) 中的两个点形成三元环。

下结论！\(n = 4\) 时，命题成立。

接下来假设一个节点 \(v\) 和 \(u, x, y, z\) 中的至少一个点相邻，此时我们假设 \(u, x, y, z\) 之间的正边我们已经连好了。我们想要证明

迭代后 \(v\) 会和 \(x, y, z\) 中的恰好两个点相邻，并且有且只有一条从 \(v\) 出发连向 \(x, y, z\) 中某一点的边，有且只有一条从 \(x, y, z\) 中某一点连向 \(v\) 的边。这两条边都是 \(v\) 与 \(x, y, z\) 之间有且只有的两条正边。

没错就是刚刚那一堆，\(u\) 换成 \(v\)。

首先明显地，\(v\) 和 \(x, y, z\) 任意一点相邻可以推出结论成立，因为和 \(u\) 的推理过程是完全相同的。

那么现在我们假定 \(v\) 和 \(u\) 相邻。发现此时有两种情况：要么是 \(v \to u \to x \operatorname{or} y\operatorname{or} z\)，要么是 \(x \operatorname{or} y\operatorname{or} z \to u \to v\)（取决于 \(u, v\) 之间边的方向）。明显再次满足迭代条件。迭代后，\(v\) 就和 \(x \operatorname{or} y \operatorname{or} z\) 相邻，再次回到熟悉的情况。（我们姑且把这个叫做二次迭代）

那么证明这个结论有什么用呢？

看图：

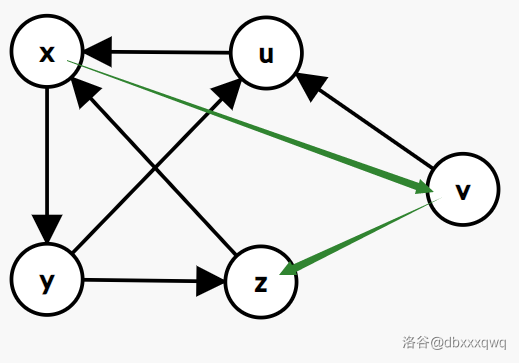
上方的绿边是我们首先连的；下方的绿边是在上方绿边后，\(v\) 和 \(x\) 相邻，于是采用了和 \(u\) 相同的手段继续。

理性探究：这样的二次迭代，还有这样一种情况：

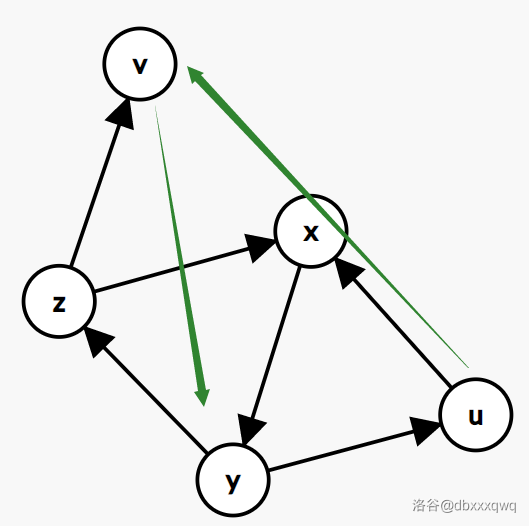
这里我们运用的仍然是对称思想——\(u\) 和 \(z\) 是完全对称的！也就是这种情况和刚刚那种情况是类似的，我们可以把 \(u\) 看成 \(z\)。

然后我们就能改写一下上面我们证明的结论……新来的节点 \(v\)，总会恰好连接到和他颜色互补的两个颜色的节点。

到这里证明就结束了，因为这个正好就是命题的另一种形式。\(n = 5\)，命题成立。

到这里你会发现有一点数学归纳思想的感觉了。同理，\(w\) 和 \(u, v, x, y, z\) 中的任何一个点相邻，会得到新来的节点 \(w\) 也总会恰好连接到和他颜色互补的两个颜色的点。\(n=6\) 命题也成立了。

因为整张图弱联通，一直这样下去，所有的点都会被讨论到。\(n\) 会一直命题成立下去。

于是这个结论就华丽证明结束了……

但是别忘了，这是一种情况。还有两种情况，分别是什么？

• 染色一切顺利，三个颜色没有染全；
• 染色时出现矛盾（染色失败）。

看起来上面那个情况（也就是第二个情况）好处理一点。其实真的很好处理，直接给出答案，你迭代不出任何边，最终的答案就是原来有多少边就是多少。

证明非常简单。采用反证法证明不存在 \(x \to y, y\to z\) 这种形式：如果存在这种形式那么就会有三种颜色。与题设矛盾。原命题得证。

这个命题得证直接说明迭代条件成立不了，寄！

于是来到最后一种情况：染色时出现矛盾。

可能会有小伙伴想象不出来这种情况，画个图举例：

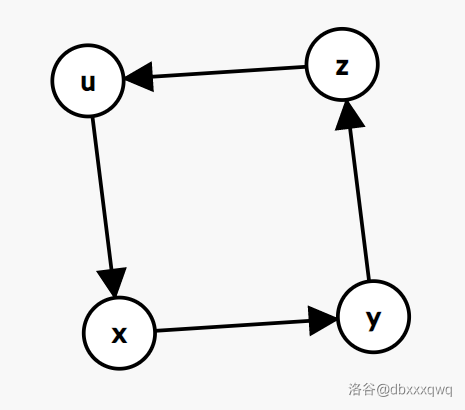
对的，就是个简单的四元环。但是你会发现你没办法把它染色成功。

比如，\(u\) 染成 \(1\)，\(x\) 染成 \(2\)，\(y\) 染成 \(3\)，\(z\) 染成 \(1\)，然后……\(z \to u\) 就寄了。。

接下来我们手动模拟一下这个图，然后你会得到一个这样的东西。。

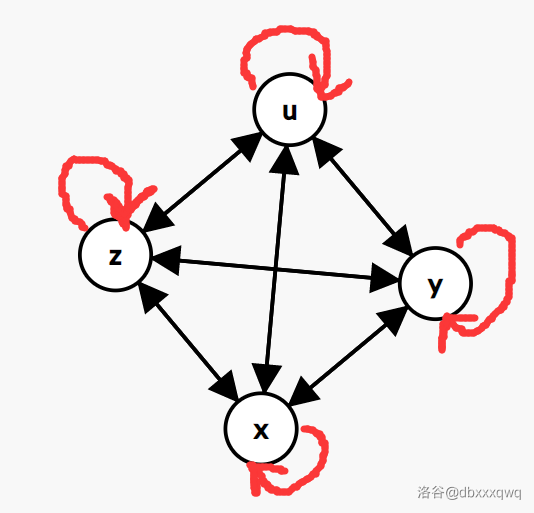
是的，什么边都能迭代出来！！

接下来开始证明：

在染色情况三中，迭代结果为完全图（包括自环）的边集。

命题：如果图中存在自环，那么迭代结果为完全图（包括自环）的边集。

证明：假设这个自环节点为 \(t\)，那么和 \(t\) 相邻的点 \(u\) 都会因为 \(u \to t \to t \to u\) 和 \(t\) 连成双向边，因为 \(u \to t \to u \to u\) 从而使得 \(u\) 形成自环。然后因为 \(u\) 是自环了，和 \(u\) 相邻的 \(v\) 肯定也会和 \(u\) 形成双向边并且 \(v\) 自身形成自环，证明和 \(u, t\) 之间相同。最后因为弱联通，相邻明显会遍布所有点，于是所有点之间都会存在双向边，所有点都有自环。

接下来考虑一般的矛盾图，我们来证明迭代后一定会产生自环，这样就能证明结论了。

首先我们可以想到，一般的矛盾图中一定存在一个弱环（不考虑边的方向就是环），这个弱环会产生矛盾。

这个很好证明，也是反证法，如果不存在弱环，那就是个树，每个节点根据父节点染色就好了，能构造出成功的染色方案。

考虑这样一个矛盾环：

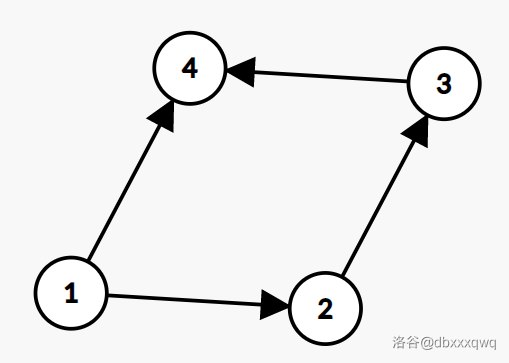
（注意和我最开始举的那个矛盾的例子是不一样的，边的方向不同）

首先这个环里肯定有类似 \(x \to y \to z\) 的状态。好的叛逆的小伙伴马上发言了，那我马上构造一个没有任何 \(x \to y \to z\) 的弱环。

那么，首先我可以证明，这个弱环的节点必须是偶数（奇数无法构造），偶数只可以构造出一种顶针的图：

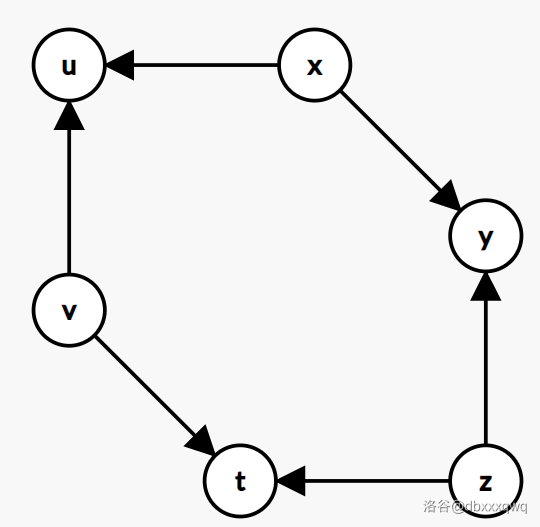
这种类似的图我们都可以构造这样一个染色方案：\(c_x = c_z = c_v = 1, c_y = c_t=c_u = 2\)。然后应该走第二种情况。

接下来继续证明。既然这个弱环存在 \(x \to y \to z\)，那么我们就迭代出一条 \(z \to x\) 的边（在这个例子里是 \(4 \to 2\)）。

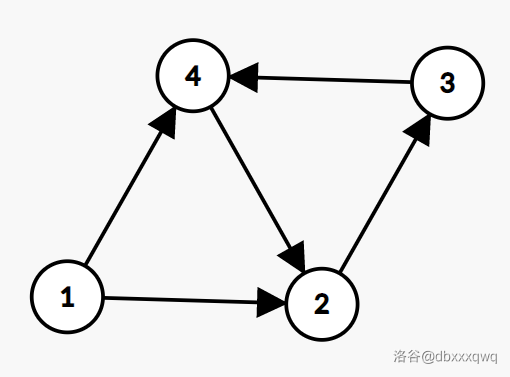
于是我们接下来关注 \(4, 1, 2\) 组成的这个小弱环——它是一定存在矛盾的。（因为 \(4, 2, 3\) 这个弱环没有问题）

同理这个弱环一定有 \(x \to y \to z\)，这个图中是 \(1 \to 4 \to 2\)，我们连接上 \(z \to x\)， 这个图中是 \(2 \to 1\)。

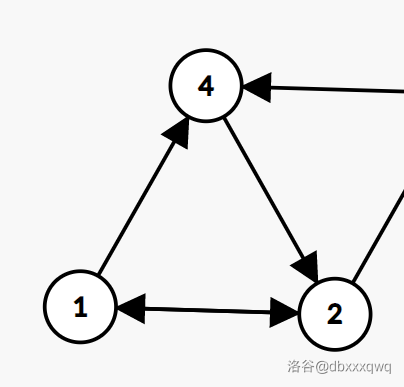
然后接着我们抛弃掉 \(4\)，找到 \(x \to y \to z\) 的 \(1 \to 2 \to 1\)，然后就 \(1 \to 1\)，喜闻乐见地得到自环。

从这个特殊再次推广到一般，我们会发现，对于染色矛盾的图：

• 图中一定有弱环；
• 矛盾的弱环中一定有 \(x \to y \to z\)；
• 可以迭代出 \(z \to x\)，那么 \(y\) 这个点就是正常的，抛弃掉 \(y\)，剩下的弱环一定矛盾，再次寻找 \(x \to y \to z\)，删掉 \(y\)；
• 经过无数次迭代，最后一定会删点删到只剩一个点，这个时候自环出现了。

证明结束。

于是到这里，我们完美证明了三种染色情况对应的结果。

第一种染色情况：所有颜色为 \(1\) 的点向所有颜色为 \(2\) 的点连边，所有颜色为 \(2\) 的点向所有颜色为 \(3\) 的点连边，所有颜色为 \(3\) 的点向所有颜色为 \(1\) 的点连边。

这里我们设颜色为 \(1\) 的点共有 \(p\) 个，颜色为 \(2\) 的点共有 \(q\) 个，颜色为 \(3\) 的点共有 \(r\) 个，那么这种情况的对应答案为 \(pq + qr + pr\)。

第二种染色情况：也就是原来的边数，直接比如是 \(m\)。（\(m\) 和题目中含义不同）

第三种染色情况：染色矛盾，此时应该是所有点都向所有点连边（包括自己），也就是点数的平方，可以说 \(n ^ 2\)。（\(n\) 和题目中含义不同）

最后考虑我们如何染色。回顾一下怎么染色的吧。

如果存在一条边 \(u \to v\)，我们的染色要使

\[c_v=\begin{cases}c_u + 1& c_u \in \{1, 2\}\\1 & c_u = 3\end{cases} \]

那么我们直接从一个点开始遍历出边 \(u \to v\)，然后对出点进行对应规则的染色就可以了。但问题在于我们给出的是弱联通块，任意一点甚至不能互相可达。

其实这个问题很好解决，初始建图时，对于 \(u \to v\)，我们建一条反边 \(v \to u\) 就可以了，遍历的时候，如果是正边，那么按照正常染色，如果是反边，那么按照反着循环染色，也就是：对于一条反边 \(u \to v\)，有

\[c_v=\begin{cases}c_u - 1& c_u \in \{2, 3\}\\3 & c_u = 1\end{cases} \]

于是这样可以保证任意一点互相可达。你是否想问可以不可以挨个没有遍历到的点为起点开始 dfs / bfs，其实稍微想一下就知道为什么不可以了（弱联通快新的部分起点应该以什么颜色开头？能否和弱联通块之前染色的那部分完美吻合？怎么区分是否在同一个弱联通块？很难处理）。

代码：

/*
 * @Author: crab-in-the-northeast 
 * @Date: 2022-07-25 02:05:23 
 * @Last Modified by: crab-in-the-northeast
 * @Last Modified time: 2022-07-25 03:15:21
 */
#include <bits/stdc++.h>
inline int read() {
    int x = 0;
    bool flag = true;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == '-')
            flag = false;
        ch = getchar();
    }
    while (isdigit(ch)) {
        x = (x << 1) + (x << 3) + ch - '0';
        ch = getchar();
    }
    if(flag)
        return x;
    return ~(x - 1);
}

const int maxm = (int)2e5 + 5; // 注意双倍建图要双倍数组大小
const int maxn = (int)1e5 + 5;

struct edge {
    int to, nxt, w;
}e[maxm];

int head[maxn], ecnt = 0;
inline void add_edge(int u, int v, int w) {
    e[++ecnt].to = v;
    e[ecnt].w = w;
    e[ecnt].nxt = head[u];
    head[u] = ecnt;
}

int c[maxn], cnt[5];
// c 数组代表第 i 个节点的颜色，注意程序中为了方便，染色使用0, 1, 2
// cnt 数组代表第 i 个颜色的节点数量，统计用

inline int cal(int u, int w) {
    return (u + w) % 3; // 计算节点 u 的后 w 个颜色
}

std :: queue <int> q;

int main() {
    std :: memset(c, -1, sizeof(c)); // -1 才表示未染色，因为 0 是颜色之一
    int m = read(), n = 0; // m 是题目中的 n，n 是题目中的 m
    while (m--) {
        int x = read(), y = read();
        add_edge(x, y, 1);
        add_edge(y, x, 2); // 在 %3 意义下相当于 -1，但是不用判断负数
        n = std :: max(n, std :: max(x, y)); // n 取最大的 x, y
    }

    long long ans = m = 0; // m 已经没有用了，这里我们用它来维护每个弱联通块的边数
    bool flag = false; // 染色是否矛盾
    for (int i = 1; i <= n; ++i) {
        if (c[i] != -1) // 如果不是新弱联通块就 continue
            continue;
        // 接下来都是从新的弱联通块中一个点开始 bfs
        cnt[0] = cnt[1] = cnt[2] = c[i] = m = 0;
        flag = false;
        q.push(i);
        while (!q.empty()) {
            int u = q.front();
            q.pop();
            ++cnt[c[u]]; // 统计 cnt
            for (int j = head[u]; j; j = e[j].nxt) {
                ++m; // 统计边
                int v = e[j].to;
                if (c[v] != -1) { // 已经染色
                    if (c[v] != cal(c[u], e[j].w)) // 矛盾
                    // 当前需要给他染的色和之前给他染的色不匹配
                        flag = true;
                } else { // 未染色
                    c[v] = cal(c[u], e[j].w); // 染色
                    q.push(v);
                }
            }
        }
        if (flag) // 情况三
            ans += 1LL * (cnt[0] + cnt[1] + cnt[2]) * (cnt[0] + cnt[1] + cnt[2]);
            // 明显地 cnt[0] + cnt[1] + cnt[2] 代表总共点数
        else if ((cnt[0] != 0) && (cnt[1] != 0) && (cnt[2] != 0)) // 情况一
            ans += 1LL * cnt[0] * cnt[1] + 1LL * cnt[1] * cnt[2] + 1LL * cnt[0] * cnt[2];
        else // 情况二
            ans += m >> 1; // 因为双倍建图所以实际边数应该是双倍的图中的边数除以2
    }
    printf("%lld\n", ans);
    return 0;
}

最终的归宿。是个结论题。

标签：颜色,自做,迭代,染色,归宿,命题,证明,正边,自切
来源： https://www.cnblogs.com/crab-in-the-northeast/p/luogu-u231111.html