筛质数（三种做法）

通常针对多个数

筛质数

给定一个正整数 $ n $，请你求出 $ 1 \sim n $ 中质数的个数。

输入格式

共一行，包含整数 $ n $。

输出格式

共一行，包含一个整数，表示 $ 1 \sim n $ 中质数的个数。

数据范围

$ 1 \le n \le 10^6 $

输入样例：

8

输出样例：

4

想法

三种筛法：

1. 朴素筛法
2. 埃氏筛法
3. 线性筛法

解法

1. 朴素筛法

时间复杂度：\(O(n\log n)\)

int p1(int n)
{
    int cnt = 0;
    for(int i = 2; i <= n; i++)
    {
        if(!st[i]) cnt ++;// 如果i是质数
        for(int j = i; j <= n; j += i) // 此数所有的倍数都是合数，直接筛掉
            st[j] = true;
    }
    return cnt;
}

2. 埃氏筛法

时间复杂度：\(O(n\log\log n)\)

此时间复杂度很低，如果\(n = 2^{32}\)，\(O(\log n)\)的算法复杂度是\(32\)，\(O(\log \log n)\)的算法复杂度是\(5\)

朴素筛法是不管你是不是合数是不是质数直接筛，但是那样会有许多重复的操作
事实上，合数不用去筛，因为合数该筛的数，它的因数已经在它前面筛完了

比如一个合数n，他的最小质因数为x，此时有一个数m是n的倍数，但是由于m是n的倍数，n是x的倍数，所以m也是x的倍数，因此，m肯定早已被x筛过了，那么n就无数可筛了

int p2(int n)
{
    int cnt = 0;
    for(int i = 2; i <= n; i++)
    {
        if(!st[i]) // 如果i是质数
        {
            cnt ++;
            for(int j = i; j <= n; j += i) // 此数所有的倍数都是合数，直接筛掉
                st[j] = true;
        }
    }
    return cnt;
}

3. 线性筛法

时间复杂度：\(O(n)\)

用埃氏筛法筛数的时候会重复筛 —— 比如\(24\)既会被\(2\)筛又会被\(3\)筛，所以我们要找到筛掉合数的唯一方法，才能避免重复筛

首先整理思路，一个合数仅会被其最小质因数筛掉，这就是线性筛法中筛掉合数的唯一方法

先看代码：

int p3(int n)
{
    for (int i = 2; i <= n; i ++ ) // 统计2-n质数的个数
    {
        if(!st[i]) primes[cnt++] = i; // 如果i是质数，那么就把i放进质数表里面
        for(int j = 0; primes[j] <= n / i; j++) // 从小到大遍历质数表，筛掉合数，直到要筛的合数比n大
        {
            // 在这层循环里，每一次我们要筛掉的合数都是primes[j] * i
            
            // i % primes[j] != 0的情况
            // 此时primes[j]不是i的最小质因数，它小于i的最小质因数，原因见下文[1]
            // 因此primes[j] * i的最小质因数就一定是primes[j]，原因见下文[2]
            st[primes[j] * i] = true; // 筛掉
            
            if(i % primes[j] == 0) break;
            // 当primes[j] 就是i的最小质因数时，应该用primes[j]筛完就break，因为后面的质数(primes[j+x])
            // 肯定都大于i的最小质因数primes[j]
            // 这个时候再用后面的质数筛(st[primes[j+x] * i] = true)的时候，
            // 筛的合数肯定就不是用最小质因数筛的了，因为i已经有了最小质因数，
            // 它可以拆解为最小质因数和另一个数的乘积，也就代表这个合数已经被前面的最小质因数筛过了
            // 所以后面的质数对答案都没有贡献，不用考虑
        }
    }
    return cnt;
}

[1]: 为什么 primes[j]不是i的最小质因数，它小于i的最小质因数？

A: 因为我们是从小到大枚举质数的，如果枚举到了i的最小质因数，它肯定会被if(i % primes[j] == 0) break; break掉，而此时还没有break，也就是还没有枚举到i的最小质因数，因此primes[j]肯定小于i的最小质因数

[2]: 为什么primes[j] < i的最小质因数时，primes[j] * i的最小质因数就一定是primes[j]？

A: 因为\(primes[j] * i\)的最小质因数肯定是\(i\)的最小质因数或者是\(primes[j]\)的最小质因数中的较小者，\(primes[j]\)是个质数，质数的最小质因数就是它本身，再看i的最小质因数，由于\(primes[j] < i\)，所以$primes[j]

• i\(的最小质因数就是\)primes[j]$

模拟：

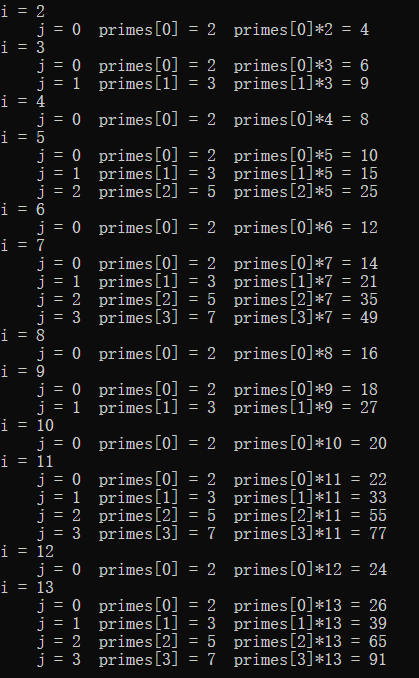
最后是三种筛法时间的对比

\(\Huge\color{Orchid}{点个赞吧！！}\)

标签：筛法,int,质数,最小,三种,做法,primes,质因数
来源： https://www.cnblogs.com/MoyouSayuki/p/16513617.html