平衡树 学习笔记
作者:互联网
\(\mathtt{Treap}\)
相较于普通的二叉搜索树,平衡树更优的点在于在二叉搜索树的基础上又给每个节点随机赋了一个优先级,并按照优先级维护一个小(或大)根堆,这样能大大减少查询时的复杂度。
\(\mathtt{Treap = Tree + Heap}\)
\(\mathtt{Treap}\) 的主要特点就是通过旋转的操作去维护平衡。其他的...代码很好理解也比较好写。
一般的操作就是插入、删除、查询某数排名、询问排名为某数的数、求前驱后继。
给出P3369 【模板】普通平衡树的代码,此处是维护了小根堆:
\(\mathtt{code}\)
在数据加强的模板题里面,上面的代码明显不行了。
主要原因是上述代码对于值相同的 \(x\) 个数会建立不同的 \(x\) 个节点,浪费很多空间,以及一些细小的地方会浪费时间。
所以就有了这份代码:(此处维护的是优先级的大根堆)
\(\mathtt{code}\)
#include<bits/stdc++.h>
using namespace std;
#define rep(i, a, b) for(int i = a; i <= b; ++i)
#define maxn 2000005
#define mod 19260817
#define inf 2000000005
struct treap{
int lft, rgh;
int d, v;
int siz, num;
}t[maxn];
int rt, tot;
int lst, ans;
int n, xi, opt, m;
inline void up(int x)
{
t[x].siz = t[t[x].lft].siz + t[t[x].rgh].siz + t[x].num;
}
inline void lft_rotate(int &x)
{
int tmp = t[x].rgh;
t[x].rgh = t[tmp].lft;
t[tmp].lft = x;
up(x);
up(tmp);
x = tmp;
}
inline void rgh_rotate(int &x)
{
int tmp = t[x].lft;
t[x].lft = t[tmp].rgh;
t[tmp].rgh = x;
up(x);
up(tmp);
x = tmp;
}
inline void insrt(int &x, int dt)
{
if(!x)
{
x = ++tot;
t[x].siz = 1, t[x].d = dt, t[x].num = 1;
t[x].v = rand();
return;
}
if(t[x].d == dt)
{
t[x].num += 1, t[x].siz += 1;
return;
}
if(dt > t[x].d)
insrt(t[x].rgh, dt);
else
insrt(t[x].lft, dt);
if(t[x].lft and t[x].v < t[t[x].lft].v)
rgh_rotate(x);
if(t[x].rgh and t[x].v < t[t[x].rgh].v)
lft_rotate(x);
up(x);
}
inline void erase(int &x, int dt)
{
if(!x) return;
if(dt < t[x].d) erase(t[x].lft, dt);
else if(dt > t[x].d) erase(t[x].rgh, dt);
else if(t[x].d == dt)
{
if(!t[x].lft and !t[x].rgh)
{
t[x].num -= 1, t[x].siz -= 1;
if(!t[x].num) x = 0;
}
else if(t[x].lft and !t[x].rgh)
{
rgh_rotate(x);
erase(t[x].rgh, dt);
}
else if(!t[x].lft and t[x].rgh)
{
lft_rotate(x);
erase(t[x].lft, dt);
}
else if(t[t[x].lft].v < t[t[x].rgh].v)
lft_rotate(x), erase(t[x].lft, dt);
else rgh_rotate(x), erase(t[x].rgh, dt);
}
up(x);
}
int cnt;
inline int fnd_rank(int x, int dt)
{
if(!x) return 1;
if(t[x].d == dt) return t[t[x].lft].siz + 1;
if(t[x].d < dt)
return t[t[x].lft].siz + t[x].num + fnd_rank(t[x].rgh, dt);
else
return fnd_rank(t[x].lft, dt);
}
inline int get_rank(int x, int rk)
{
if(!x) return 0;
if(t[t[x].lft].siz >= rk)
return get_rank(t[x].lft, rk);
else if(t[t[x].lft].siz + t[x].num < rk)
return get_rank(t[x].rgh, rk - t[x].num - t[t[x].lft].siz);
else return t[x].d;
}
inline int pre(int x, int dt)
{
if(!x) return -inf;
if(t[x].d >= dt) return pre(t[x].lft, dt);
return max(t[x].d, pre(t[x].rgh, dt));
}
inline int suc(int x, int dt)
{
if(!x) return inf;
if(t[x].d <= dt) return suc(t[x].rgh, dt);
return min(t[x].d, suc(t[x].lft, dt));
}
int main()
{
scanf("%d%d", &n, &m);
rep(i, 1, n)
scanf("%d", &xi),
insrt(rt, xi);
rep(i, 1, m)
{
scanf("%d%d", &opt, &xi);
xi ^= lst;
bool flg = 1;
if(opt == 1) insrt(rt, xi), flg = 0;
if(opt == 2) erase(rt, xi), flg = 0;
if(opt == 3)
lst = fnd_rank(rt, xi);
if(opt == 4)
lst = get_rank(rt, xi);
if(opt == 5)
lst = pre(rt, xi);
if(opt == 6)
lst = suc(rt, xi);
if(flg) ans ^= lst;
}
printf("%d\n", ans);
return 0;
}
\(\mathtt{Splay}\)
平摊复杂度都是 \(O(log2n)\)的。
与 \(\mathtt{Treap}\) 不同的是,它通过双旋来维持平衡树的性质,而不是给每个节点随机赋优先值。
放两张图比较单旋与双旋。


与 \(\mathtt{Treap}\) 相比,它代码简单,空间需求较小,常用。
具体的、详细的 \(\mathtt{Splay}\) 博客可以看 yyb 写的这篇。
模板题(无数据加强)代码:\(\mathtt{code}\)
#include<bits/stdc++.h>
using namespace std;
#define rep(i, a, b) for(register int i = a; i <= b; ++i)
const int inf = 2147483647;
const int maxn = 500100;
int n;
struct node{
int sn[2];
int siz, fa;
int val, cnt;
}t[maxn];
int tot;
int rt;
inline void up(int x)
{
t[x].siz = t[t[x].sn[0]].siz + t[t[x].sn[1]].siz + t[x].cnt;
}
inline void rotate(int x)
{
int y = t[x].fa;
int z = t[y].fa;
int kx = (x == t[y].sn[1]), ky = (y == t[z].sn[1]);
t[z].sn[ky] = x, t[x].fa = z;
t[y].sn[kx] = t[x].sn[kx ^ 1], t[t[x].sn[kx ^ 1]].fa = y;
t[x].sn[kx ^ 1] = y, t[y].fa = x;
up(y), up(x);
}
inline void splay(int x/*移动的节点编号*/, int gl/*目标位置的父亲编号(若为 0则移至根节点)*/)
{
while(t[x].fa != gl)
{
int y = t[x].fa;
int z = t[y].fa;
if(z != gl)
(t[z].sn[0] == y) ^ (t[y].sn[0] == x) ? rotate(x) : rotate(y);
rotate(x);
}
if(!gl) rt = x;
}
inline void insrt(int x)
{
int u = rt, ft = 0;
while(u and t[u].val != x)
ft = u,
u = t[u].sn[x > t[u].val];
if(u) t[u].cnt += 1;
else
{
u = ++tot;
if(ft)
t[ft].sn[x > t[ft].val] = u;
t[tot].cnt = t[tot].siz = 1,
t[tot].fa = ft,
t[tot].val = x;
t[tot].sn[0] = t[tot].sn[1] = 0;
}
splay(u, 0);
}
inline void find(int x)
{
int u = rt;
if(!u) return;
while(t[u].sn[x > t[u].val] and t[u].val != x)
u = t[u].sn[x > t[u].val];
splay(u, 0);
}
inline int affix(int x, int d)
{
find(x);
int u = rt;
if((t[u].val < x and !d) or (t[u].val > x and d))
return u;
u = t[u].sn[d];
while(t[u].sn[d ^ 1])
u = t[u].sn[d ^ 1];
return u;
}
inline void erase(int x)
{
int pre = affix(x, 0), nxt = affix(x, 1);
splay(pre, 0), splay(nxt, pre);
int dl = t[nxt].sn[0];
if(t[dl].cnt > 1)
t[dl].cnt -= 1, splay(dl, 0);
else t[nxt].sn[0] = 0;
}
inline int k_th(int k)
{
int u = rt;
if(t[u].siz < k) return 0;
while(1)
{
int ls = t[u].sn[0];
if(k > t[ls].siz + t[u].cnt)
k -= t[ls].siz + t[u].cnt,
u = t[u].sn[1];
else
if(k <= t[ls].siz)
u = ls;
else return t[u].val;
}
}
int main()
{
insrt(-2147483647), insrt(+2147483647);
scanf("%d", &n);
rep(i, 1, n)
{
int opt, x;
scanf("%d%d", &opt, &x);
if(opt == 1) insrt(x);
if(opt == 2) erase(x);
if(opt == 3)
find(x), printf("%d\n", t[t[rt].sn[0]].siz);
if(opt == 4)
printf("%d\n", k_th(x + 1));
if(opt == 5)
printf("%d\n", t[affix(x, 0)].val);
if(opt == 6)
printf("%d\n", t[affix(x, 1)].val);
}
return 0;
}
\(\mathtt{fhq\ Treap}\)
即无旋 \(\mathtt{Treap}\),通过两个操作—— \(\mathtt{split}\)(分裂)和 \(\mathtt{merge}\)(合并)来维护 \(\mathtt{BST}\) 以及优先值的小根堆。
此处放上两个白嫖来的动图供深刻理解一下。(俩动图的原博客)
不过值得注意的是,分裂有两种:
- 按照值的大小来分裂:假如分裂标准是值 \(k\),那么权值小于等于 \(k\) 的点会被分到左子树,其余的点被分到右子树。
- 把前 \(k\) 个节点分到左边,其余的分到右边。
关于第二种的分裂方式,详见上面的博客链接,其代码编写方式与查找排名相似。
模板题(无数据加强)代码:
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 5;
struct node{
int ch[2];
int val, siz;
int d;
}t[maxn];
int rt;
int n;
int opt, tmp;
int tot;
int x, y, z;
inline void up(int x)
{
t[x].siz = t[t[x].ch[0]].siz + t[t[x].ch[1]].siz + 1;
}
inline int build(int x)
{
t[++tot].val = x;
t[tot].d = rand(), t[tot].siz = 1;
return tot;
}
inline void split(int nw, int k, int &x, int &y)
{
if(!nw) x = y = 0;
else if(k >= t[nw].val)
x = nw, split(t[nw].ch[1], k, t[nw].ch[1], y);
else y = nw, split(t[nw].ch[0], k, x, t[nw].ch[0]);
if(nw) up(nw);
}
inline int merge(int x, int y)
{
if(!x or !y) return x + y;
if(t[x].d < t[y].d)
{
t[x].ch[1] = merge(t[x].ch[1], y);
up(x);
return x;
}
else
{
t[y].ch[0] = merge(x, t[y].ch[0]);
up(y);
return y;
}
}
inline int kth(int nw, int x)
{
while(1)
{
if(x <= t[t[nw].ch[0]].siz)
nw = t[nw].ch[0];
else if(x == t[t[nw].ch[0]].siz + 1)
return nw;
else
x -= t[t[nw].ch[0]].siz + 1, nw = t[nw].ch[1];
}
}
int main()
{
// srand((unsigned)time(NULL));有没有这句都行
scanf("%d", &n);
while(n--)
{
scanf("%d%d", &opt, &tmp);
if(opt == 1)
{
split(rt, tmp, x, y);
rt = merge(merge(x, build(tmp)), y);
}
if(opt == 2)
{
split(rt, tmp, x, z), split(x, tmp - 1, x, y);
y = merge(t[y].ch[0], t[y].ch[1]);
rt = merge(merge(x, y), z);
}
if(opt == 3)
{
split(rt, tmp - 1, x, y);
printf("%d\n", t[x].siz + 1);
rt = merge(x, y);
}
if(opt == 4) printf("%d\n", t[kth(rt, tmp)].val);
if(opt == 5)
{
split(rt, tmp - 1, x, y);
printf("%d\n", t[kth(x, t[x].siz)].val);
merge(x, y);
}
if(opt == 6)
{
split(rt, tmp, x, y);
printf("%d\n", t[kth(y, 1)].val);
merge(x, y);
}
}
return 0;
}
文艺平衡树
用平衡树实现区间内的操作——翻转区间。用 \(\mathtt{Splay}\) 实现。
因为它给定了序列,所以无需按照权值大小建树,按照点编号仿照线段树的方式建树即可。
至于翻转区间,假设我们要翻转的区间是 \([l,r]\),那么:
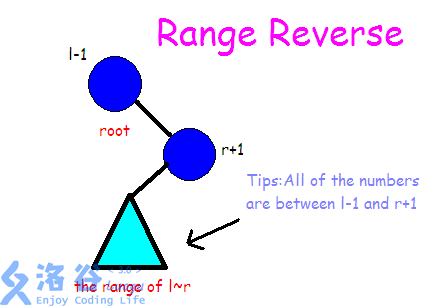
(注:小花的图)
然后像线段树一样,给它打上一个 \(lazytag\),表示要旋转。这就意味着之后在操作前都要 \(push\ down\)。
对于当前节点的翻转,只需要交换其左右子节点的编号即可。
#include<bits/stdc++.h>
using namespace std;
#define rep(i, a, b) for(int i = a; i <= b; ++i)
const int maxn = 1e5 + 5;
const int inf = 2147483647;
int n, m;
int a[maxn];
struct node{
int ch[2];
int fa;
int siz, tag;
int val;
}t[maxn];
int rt, tot;
inline void up(int x)
{
t[x].siz = t[t[x].ch[0]].siz + t[t[x].ch[1]].siz + 1;
}
inline void push_down(int x)
{
if(!t[x].tag) return;
t[t[x].ch[0]].tag ^= 1;
t[t[x].ch[1]].tag ^= 1;
swap(t[x].ch[0], t[x].ch[1]);
t[x].tag = 0;
}
inline void rotate(int x)
{
int y = t[x].fa, z = t[y].fa;
push_down(y), push_down(x);
int kx = (x == t[y].ch[1]), ky = (y == t[z].ch[1]);
t[z].ch[ky] = x, t[x].fa = z;
t[y].ch[kx] = t[x].ch[kx ^ 1], t[t[x].ch[kx ^ 1]].fa = y;
t[x].ch[kx ^ 1] = y, t[y].fa = x;
up(y), up(x);
}
inline void splay(int x, int gl)
{
while(t[x].fa != gl)
{
int y = t[x].fa, z = t[y].fa;
if(z != gl)
(y == t[z].ch[1]) ^ (x == t[y].ch[1]) ? rotate(x) : rotate(y);
rotate(x);
}
if(!gl) rt = x;
}
inline int build(int l, int r, int ff)
{
if(l > r) return 0;
int nw = ++tot, mid = (l + r) >> 1;
t[nw].fa = ff, t[nw].val = a[mid];
t[nw].ch[0] = t[nw].ch[1] = 0;
t[nw].ch[0] = build(l, mid - 1, nw);
t[nw].ch[1] = build(mid + 1, r, nw);
up(nw);
return nw;
}
inline int find (int x)
{
int u = rt;
while(531)
{
push_down(u);
if(x <= t[t[u].ch[0]].siz) u = t[u].ch[0];
else
{
x -= t[t[u].ch[0]].siz + 1;
if(!x) return u;
u = t[u].ch[1];
}
}
}
inline void reverse(int l, int r)
{
l -= 1, r += 1;
l = find(l), r = find(r);
splay(l, 0), splay(r, l);
t[t[t[rt].ch[1]].ch[0]].tag ^= 1;
}
inline void output(int nw)
{
if(!nw) return;
push_down(nw);
output(t[nw].ch[0]);
if(t[nw].val != inf and t[nw].val != -inf)
printf("%d ", t[nw].val);
output(t[nw].ch[1]);
}
int main()
{
scanf("%d%d", &n, &m);
rep(i, 1, n) a[i + 1] = i;
a[1] = -inf, a[n + 2] = inf;
rt = build(1, n + 2, 0);
rep(i, 1, m)
{
int x, y;
scanf("%d%d", &x, &y);
reverse(x + 1, y + 1);
}
output(rt);
return 0;
}
替罪羊树
抛开这奇怪的名字不看, 替罪羊树不依赖旋转来维护树的平衡,而是暴力重构。所以码量相比之下大多了。
定义一个平衡因子 \(alpha\),且当以 \(u\) 为根的树的一以 \(v\) 为根节点的子树满足:\(t[v].size > t[u].size* alpha\) 时,将子树 \(u\) 拍扁——中序遍历存入一个数组(该数组有序),然后仿照线段树的建树方式(每次取序列中点作为当前节点),使子树 \(u\) 的深度不超过 \(logn\)。
还有如果要删除的节点过多也要重构。
还有比较特别的一点,在删除某一节点时,因为替罪羊树没有旋转操作,所以我们只能暂且给它打上一个删除标记,若后边有包含它的重构操作,则在重构时忽略它即可。
剩下的看代码注释。
#include<bits/stdc++.h>
using namespace std;
#define rep(i, a, b) for(int i = a; i <= b; ++i)
const double alpha = 0.75;
const int maxn = 1000010;
int n;
int tot, rt;
int cnt, ck[maxn];
struct node{
int l, r;
int fa, res, val;
int tf;//删除标记
int siz/*子树节点数总和*/, tsiz/*子树中没有被删除的节点数*/, nsiz/*一共含有多少个数*/;
}t[maxn];
struct node2{
int tot, val;
}sl[maxn];//拍扁时的存储数组
int ans;
int num;
inline int kk()//获取新节点的编号
{
if(cnt > 0) return ck[cnt--];//回收节点再利用
return ++tot;
}
inline void build(int x, int y, int fa)//建立一个编号为 y,值为 x的节点
{
t[y].val = x, t[y].fa = fa;
t[y].siz = t[y].tsiz = t[y].nsiz = t[y].res = 1;
t[y].l = t[y].r = t[y].tf = 0;
}
inline void updata(int v, int x, int y, int z)//一路更新到根节点
{
if(!v) return;
t[v].siz += x, t[v].tsiz += y, t[v].nsiz += z;
updata(t[v].fa, x, y, z);
}
inline int find(int nw, int x)
{
if(t[nw].val > x and t[nw].l) return find(t[nw].l, x);
if(t[nw].val < x and t[nw].r) return find(t[nw].r, x);
return nw;
}
inline void dfs_rebuild(int x)//拍扁该树,存入数组
{
if(!x) return;
dfs_rebuild(t[x].l);
if(!t[x].tf)
{
sl[++num].tot = t[x].res;
sl[num].val = t[x].val;
}
ck[++cnt] = x;
dfs_rebuild(t[x].r);
}
inline int readd(int l, int r, int fa)//重构子树
{
if(l > r) return 0;
int mid = (l + r) >> 1, nw = kk();
t[nw].res = sl[mid].tot, t[nw].val = sl[mid].val;
t[nw].fa = fa, t[nw].tf = 0;
t[nw].l = readd(l, mid - 1, nw), t[nw].r = readd(mid + 1, r, nw);
t[nw].siz = t[nw].tsiz = r - l + 1;
t[nw].nsiz = t[t[nw].l].nsiz + t[t[nw].r].nsiz + t[nw].res;
return nw;
}
inline void rebuild(int x)//重构子树 x
{
num = 0;
dfs_rebuild(x);
if(rt == x) rt = readd(1, num, 0);
else
{
updata(t[x].fa, -t[x].siz + t[x].tsiz, 0, 0);
if(t[t[x].fa].l == x) t[t[x].fa].l = readd(1, num, t[x].fa);
else t[t[x].fa].r = readd(1, num, t[x].fa);
}
}
inline void find_rebuild(int nw, int x)//寻找需要重构的子树
{
if((double)t[t[nw].l].siz > (double)t[nw].siz * alpha or (double)t[t[nw].r].siz > (double)t[nw].siz * alpha or ((double)t[nw].siz - (double)t[nw].tsiz) > (double)t[nw].siz * 0.4)
{
rebuild(nw);
return;
}
if(t[nw].val != x) find_rebuild(x < t[nw].val ? t[nw].l : t[nw].r, x);
}
inline void add(int x)//添加节点
{
if(!rt)
{
build(x, rt = kk(), 0);
return;
}
int p = find(rt, x);
if(x == t[p].val)
{
t[p].res += 1;
if(t[p].tf) t[p].tf = 0, updata(p, 0, 1, 1);
else updata(p, 0, 0, 1);
}
else if(x < t[p].val) build(x, t[p].l = kk(), p), updata(p, 1, 1, 1);
else build(x, t[p].r = kk(), p), updata(p, 1, 1, 1);
find_rebuild(rt, x);
}
inline void delet(int x)//删除节点
{
int p = find(rt, x);
t[p].res -= 1;
if(!t[p].res) t[p].tf = 1, updata(p, 0, -1, -1);
else updata(p, 0, 0, -1);
find_rebuild(rt, x);
}
inline void rnk(int x)
{
int p = rt, rk = 0;
while(t[p].val != x)
{
if(x < t[p].val) p = t[p].l;
else rk += t[t[p].l].nsiz + t[p].res, p = t[p].r;
}
rk += t[t[p].l].nsiz;
printf("%d\n", rk + 1);
}
inline void k_th(int x)
{
int p = rt;
while(531)
{
if(x <= t[t[p].l].nsiz) p = t[p].l;
else
{
x -= t[t[p].l].nsiz;
if(x <= t[p].res)
{
printf("%d\n", t[p].val);
return;
}
x -= t[p].res, p = t[p].r;
}
}
}
inline void dfsl(int x)
{
if(t[x].r) dfsl(t[x].r);
if(ans) return;
if(!t[x].tf)
{
printf("%d\n", t[x].val), ans = 1;
return;
}
if(t[x].l) dfsl(t[x].l);
}
inline void dfsr(int x)
{
if(t[x].l) dfsr(t[x].l);
if(ans) return;
if(!t[x].tf)
{
printf("%d\n", t[x].val), ans = 1;
return;
}
if(t[x].r) dfsr(t[x].r);
}
/*
先找到值为x的节点,然后看看有没有左儿子,如果有,就将左子树遍历一遍,
顺序是:右儿子->根->左儿子,找到的第一个没有被删除的节点就是答案。
*/
inline void pre(int nw, int x, int fl)
{
if(!fl)
{
pre(t[nw].fa, x, (t[t[nw].fa].r == nw));
return;
}
if(!t[nw].tf and t[nw].val < x)
{
printf("%d\n", t[nw].val);
return;
}
if(t[nw].l)
{
ans = 0, dfsl(t[nw].l);
return;
}
pre(t[nw].fa, x, t[t[nw].fa].r == nw);
}
inline void nxt(int nw, int x, int fl)
{
if(!fl)
{
nxt(t[nw].fa, x, (t[t[nw].fa].r != nw));
return;
}
if(!t[nw].tf and t[nw].val > x)
{
printf("%d\n", t[nw].val);
return;
}
if(t[nw].r)
{
ans = 0, dfsr(t[nw].r);
return;
}
nxt(t[nw].fa, x, t[t[nw].fa].r != nw);
}
int main()
{
scanf("%d", &n);
rep(i, 1, n)
{
int opt, x;
scanf("%d%d", &opt, &x);
if(opt == 1) add(x);
if(opt == 2) delet(x);
if(opt == 3) rnk(x);
if(opt == 4) k_th(x);
if(opt == 5) pre(find(rt, x), x, 1);
if(opt == 6) nxt(find(rt, x), x, 1);
}
return 0;
}
标签:return,val,int,siz,笔记,学习,inline,平衡,nw 来源: https://www.cnblogs.com/gsn531/p/16497419.html