【数据结构】线段树分治

目录

线段树分治

本题做法

实现

线段树分治

事实上线段树分治的做法很简单，就是在时间轴上开线段树，以方便处理在一段时间内其效果的操作。

比如说，现在整棵线段树维护的时间范围是 \([1, 3]\)，开出的线段树自然是：

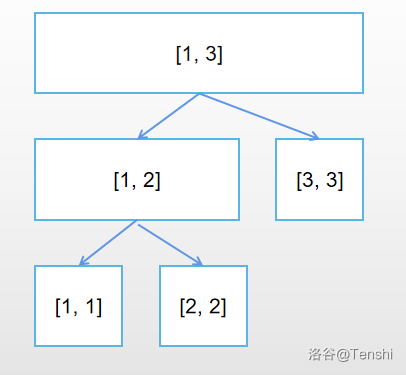
现在有一个操作在时间 \([1, 2]\) 上作用，那么对应于线段树的节点就是：

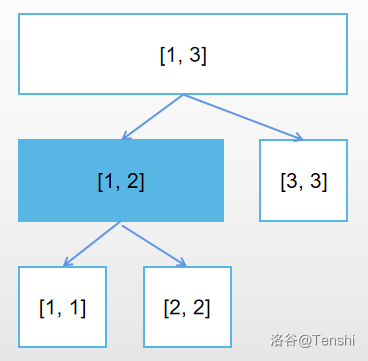
又有一个操作在时间 \([2, 3]\) 上作用，对应于线段树的节点就是：

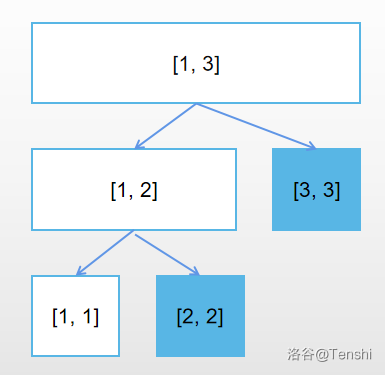
根据线段树的性质，每个操作至多被划分成 \(\rm{log}\) 个线段树节点上的操作，我们就将划分后的操作依次存入发生影响的线段树节点即可。

最后，我们先序遍历一遍这棵树，对于当前节点，使其存储的操作生效，然后在递归地访问左右子树后撤销即可。（这一步使用一个栈进行维护，操作生效时压栈，最后在弹栈的时候执行撤销）

本题做法

本题的操作是在一段时间内合并图上的两点（也就是连边），然后判断某时间是否为二分图，结合上面的线段树分治过程，直接在图上维护（例如考虑染色）当然很不方便。因此考虑使用扩展域并查集维护：而为了方便撤销操作，我们不可以进行路径压缩，只能采取按秩合并。

实现

实现的思路是：

• 先在时间轴 \([1, K]\) 建立线段树。

• 首先将操作分配（assign）进线段树节点的 vector<pii> o 中。

• 然后对整棵树进行询问，并相应地进行操作生效（这题是合并，也就是代码中的 merge）、撤销（resume）操作，

  • 如果当前区间会导出矛盾，那么我们可以直接在这个区间都输出 No。
  • 否则，继续向左右子树递归直到叶节点，如果直到叶节点都没有矛盾，直接输出 Yes。
  • 可以发现，因为是先序遍历，所以直接输出就能满足题目的输出要求。

// Problem: P5787 二分图 /【模板】线段树分治
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5787
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
 
#define debug(x) cerr << #x << ": " << (x) << endl
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define dwn(i,a,b) for(int i=(a);i>=(b);i--)
#define pb push_back
#define all(x) (x).begin(), (x).end()
 
#define x first
#define y second
using pii = pair<int, int>;
using ll = long long;
 
inline void read(int &x){
    int s=0; x=1;
    char ch=getchar();
    while(ch<'0' || ch>'9') {if(ch=='-')x=-1;ch=getchar();}
    while(ch>='0' && ch<='9') s=(s<<3)+(s<<1)+ch-'0',ch=getchar();
    x*=s;
}

const int N=2e5+50;

int n, m, K;

struct Msg{
	int x, y, z;
}stk[N];
int top;

struct Dsu{
	int fa[N], rk[N];
	
	void init(){
		rep(i,1,n<<1) fa[i]=i, rk[i]=1;
	}
	
	int find(int x){
		return x==fa[x]? x: find(fa[x]);
	}
	
	bool same(int x, int y){
		return find(x)==find(y);
	}
	
	void merge(int x, int y){
		x=find(x), y=find(y);
		if(x==y) return;
		if(rk[x]>rk[y]) swap(x, y);
		fa[x]=y;
		stk[++top]={x, y, rk[x]==rk[y]};
		if(rk[x]==rk[y]) rk[y]++;
	}
	
	void resume(Msg t){
		rk[t.y]-=t.z;
		fa[t.x]=t.x;
	}
}dsu;

struct Node{
	int l, r;
	vector<pii> o;
	
	#define ls u<<1
	#define rs u<<1|1
}tr[N<<2];

void build(int u, int l, int r){
	tr[u]={l, r};
	if(l==r) return;
	int mid=l+r>>1;
	build(ls, l, mid), build(rs, mid+1, r);
}

void assign(int u, int l, int r, int x, int y){
	if(l<=tr[u].l && tr[u].r<=r){
		tr[u].o.pb({x, y});
		return;
	}
	int mid=tr[u].l+tr[u].r>>1;
	if(l<=mid) assign(ls, l, r, x, y);
	if(mid<r) assign(rs, l, r, x, y);
}

void divi(int u){
	bool ng=false;
	int pre=top;
	for(auto &[x, y]: tr[u].o){
		dsu.merge(x, y+n);
		dsu.merge(y, x+n);
		if(dsu.same(x, x+n) || dsu.same(y, y+n)){
			ng=true;
			break;
		}
	}
	if(ng) rep(i,tr[u].l,tr[u].r) puts("No");
	else{
		if(tr[u].l==tr[u].r) puts("Yes");
		else{
			divi(ls);
			divi(rs);
		}
	}
	while(top!=pre){
		dsu.resume(stk[top--]);
	}
}

signed main(){
	cin>>n>>m>>K;
	build(1, 1, K);
	dsu.init();
	
	rep(i,1,m){
		int x, y, l, r; read(x), read(y), read(l), read(r);
		if(++l>r) continue;
		assign(1, l, r, x, y);
	}
	divi(1);
	
	return 0;
}

标签：int,线段,分治,define,操作,数据结构,节点,rk
来源： https://www.cnblogs.com/Tenshi/p/16471851.html