P4260 [Code+#3]博弈论与概率统计 题解

楼上的 dalao 的题解中的式子几乎推得完美，这篇题解主要进行细节补充与概述方便大家理解。

题目概述：

求 \(A\) 在比 \(N+M\) 场赛中胜利 \(N\) 场的得分期望（胜利得 \(1\) 分，失败扣 \(1\) 分，存在保护机制，即到 \(0\) 分再失败不会扣分）。

预备知识：

期望，卡特兰数，费马小定理求逆元，杨辉三角与组合数，莫队。

不过相信点进这道题的你这些对你都不成问题。

题目分析：

\(A\) 的得分期望就是所有情况下 \(A\) 的得分除以 \(C_{n+m}^{n}\) ，问题转化为求所有情况下 \(A\) 的得分和。

我们从 \(A\) 的最大得分情况开始分析，可知 \(A\) 的最大得分时的方案为开局 \(m\) 场全输，后面 \(n\) 场全赢，因为开局分为 \(0\) ，一直触发保护机制不扣分，所以最大得分为 \(n\) 。

所以从 \(n-m\) 分开始，每多得一分都是吃了一次保护机制。

我们可以构造一个类似于卡特兰数的图像，设定向上走为 \(A\) 胜利，向右走为 \(B\) 胜利，最终到达点 \((n,m)\) 本局结束。

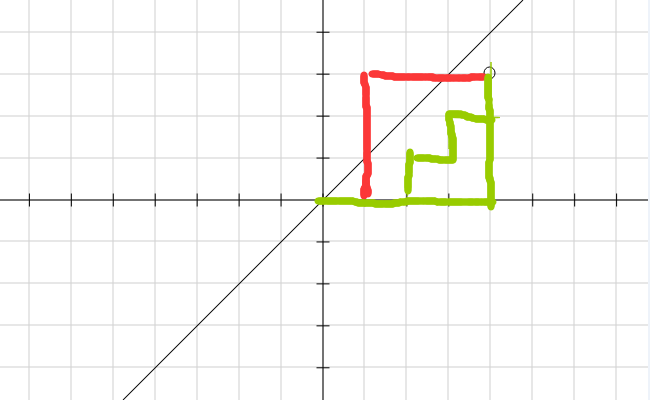
图中两条绿线在构造直线下到达终点 \((n,m)\) ，为合法方案，图中红线越过了直线，为非法方案。

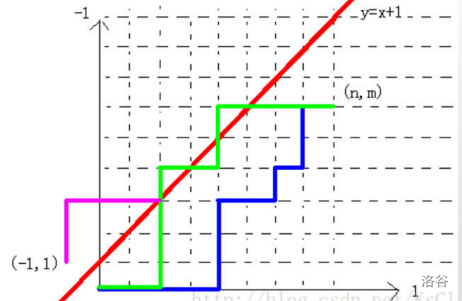
同理，我们推广到 \(A\) 得分为 \(n-m+1\) 时就是将直线向上平移 \(1\)，简单容斥我们可得到此时的合法方案就是通过了它平移前的直线且没有通过平移后的直线所构成的合法方案。

我们可以通过对称起点，构造所有不合法的方案（下图中粉线），针对平移后的直线合法方案就是所有方案减去非法方案，即： \(ans = \sum_{i=0}^{m} (C_{n+m}^{n+i} - C_{n+m}^{n+i+1})(n-m+i)\) ，通过错位相减，我们可以将原式化为： \(ans = (n-m) C_{n+m}^{n} + \sum_{i=0}^{m-1} C_{n+m}^{i}\)。

发现 \((n-m) C_{n+m}^{n}\) 可以处理出来，问题就转化为如何快速处理 \(\sum_{i=0}^{m-1} C_{n+m}^{i}\) ，设\(f(n,k) = \sum_{i=0}^{k} C_{n}^{i}\) ，我们将 \(n,k\) 看做一个二维平面，发现点 \((n,k)\) 到 \((n,k-1)\) 与 \((n,k+1)\) 可以加减 \(C_{n}^{k+1}\) 与 \(C_{n}^{k}\) 直接得来，又根据杨辉三角 \(f(n,k) = \sum_{i=0}^{k} (C_{n-1}^{i-1} + C_{n-1}^{i}) = 2 \times f(n-1,k) - C_{n-1}^{k}\) 来快速维护点 \((n,k)\) 到 \((n-1,k)\) 与 \((n+1,k)\) ，我们可以使用莫队维护。

本题可以看做卡特兰数的拓展运用，同时也告诉我们莫队不只是单纯的离线区间维护算法。简单说一下第二类斯特林数做法的不可行性，我们可以认为它所包含的方案是所有与构造直线有交点的合法方案，而少统计了如图一两条绿线一样的不与直线相交的情况。

代码有压行，但逻辑相同的部分多在同一行，自认为存在部分可读性。

Code.

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=3e5+10,mod=1e9+7;
int T,p,x[N],y[N],ans[N],len,fin[N],l,ifin[N],res=2;
int get(int x) {return x/len;} struct node {int x,k,id;} q[N];
inline int ksm(int a,int b) {int res=1; while(b) {if(b&1) res=(res*a)%mod; a=(a*a)%mod; b>>=1;} return res;}
bool cmp(node a,node b) {if(get(a.x) == get(b.x)) return a.k < b.k; return a.x < b.x;}
inline int C(int n,int k) {if(n < k) return 0; return ((fin[n]*ifin[n-k])%mod*ifin[k])%mod;}
signed main()
{
	scanf("%lld%lld",&T,&p);
	for(int i=1;i<=T;i++)
	{
		scanf("%lld%lld",&x[i],&y[i]);
		q[i].x=x[i]+y[i]; q[i].id=i; l=max(l,q[i].x); q[i].k=min(x[i],y[i])-1;
	}
	len=max(1LL,(int)sqrt(l)); sort(q+1,q+T+1,cmp);
	fin[0]=1; for(int i=1;i<=l;i++) fin[i]=fin[i-1]*i%mod;
    ifin[l]=ksm(fin[l],mod-2); for(int i=l;i>=1;i--) ifin[i-1]=ifin[i]*i%mod;
	for(int i=1;i<=T;i++) if(x[i]>=y[i]) ans[i]=(x[i]-y[i])*C(x[i]+y[i],x[i])%mod;
	int n=1,k=1,i2=ksm(2,mod-2);
	for(int i=1;i<=T;i++)
	{
		int n1=q[i].x,k1=q[i].k;
        while(n > n1) res=(res+C(n-1,k))*i2%mod,n--;
        while(n < n1) res=(res*2-C(n,k)+mod)%mod,n++;
        while(k > k1) res=(res-C(n,k)+mod)%mod,k--;
        while(k < k1) res=(res+C(n,k+1))%mod,k++;
        ans[q[i].id]=(ans[q[i].id]+res)%mod;
    }
	for(int i=1;i<=T;i++) printf("%lld\n",(ans[i]*ksm(C(x[i]+y[i],x[i]),mod-2)%mod)%mod);
	return 0;
}

标签：+#,方案,Code,return,int,题解,ans,res,mod
来源： https://www.cnblogs.com/EastPorridge/p/16468633.html