mathematica 一些方法归纳
作者:互联网
声明:本笔记来自很多网上的文章或书,由于当时记笔记的时候忘记写来源,所以此笔记中有些内容可能没注明来源,抱歉,若有侵权,请联系本人。另外,以下写得比较乱,抱歉
0.帮助文档有时候省略一些重要东西,所以mathematica遇到问题除了帮助文档,就去网上找更好!!!
比如清除的命令clearall、clear等不能清除带下标的量,这个重要的注意事项帮助文档中就确实没有。
所以mathematica遇到问题就去网上找更好!!!
1.mathematica书
我也不是用mathematica来编程,编程是用python,我只是用mathematica来推导公式,不会有更多需要用到的时候。所以临时学就可以,重要的是物理!!!不浪费时间,
最简单的入门:
高级:
mathematica很多功能可以在帮助文档中学,比如定义函数、清除变量赋值等等,但有时候帮助文档太简单,比如怎么设置样式表,怎么分页,等等内容,见:科学文库中:WOLFRAM MATHEMATICA 实用编程指南(官方的书,积累了几十年经验)这本就够了
其英文版:Hands-On Start to Wolfram Mathematica And Programming with the Wolfram Language by Cliff Hastings, Kelvin Mischo, Michael Morrison 我也下载了
与物理有关:
Mathematica 10.3与数字化大学物理 by 江俊勤:不知道这本怎么样
在对以上物理问题进行研究的同时,作者也力求通过各个实例向读者介绍数字化物理的基本方法、程序设计的基本思想及 Ma也ematica 中一些重要命令和函数的使用技巧(有些技巧在现有文献资料中尚未见有相关介绍,属于首例)
理论物理有关:
没有相关的书,这本不是软件:Mathematica for Theoretical Physics Electrodynamics, Quantum Mechanics, General Relativity, and Fractals Volume 2 by Baumann, Gerd (z-lib.org)
群论、固体物理有关:
\Group Theory in Solid State Physics and Photonics Problem Solving with Mathematica by Wolfram Hergert, R. Matthias Geilhufe (z-lib.org).pdf
前言:几乎所有的物理学分支都存在对称原理。在固态p h y s i c s,f o re x a m p l e,w e h a v e t o t a k e t o a c o n t h e s y m e t r o f r r y s t a l s,c l s s,或最近发现的结构,如富勒烯,碳纳米管或准晶。如果没有对称性的论证,高能物理和基本粒子标准模型的发展将是不可想象的。群论是用来描述对称性的数学方法。因此,在过去的一个世纪里,它已经成为物理学家的重要工具。在某些情况下,理解群论的基本概念可能会变得有点累。一个原因是,与组的定义和特殊结构以及应用相关的练习要么微不足道,要么很快变得乏味,即使具体的计算大多是初级的。尤其是当教科书没有提供额外的帮助和特殊工具来帮助读者熟悉内容时,就会出现这种情况。因此,我们为本书选择了不同的方法。我们的意图不是写另一篇关于固态物理中群论的综合文本,而是一篇基于Mathematica包GTPack的更实用的文本。因此,这本书更像是一本关于群论计算方法的手册,通过GTPack命令解释了固态物理中所有基本概念和对称性相关问题的解决方案。考虑到手稿的长度,我们在某些地方省略了更长的技术证明。然而,感兴趣的读者在这些情况下会参考更严格的教科书,我们会提供具体的参考。本书中的例子和任务旨在鼓励读者积极使用GTPack。GTPackitself为标准的Mathematica语言提供了200多个附加模块。内容从基本群论和表象理论到更实用的方法,如晶体场理论、紧束缚和平面波方法,再到固体物理和光子学领域基于对称性的研究。GTPack可通过GTPack.org在线免费获得。t h e p a c k a g e I s d e s I g n e d t o b e a s I l y c e s s I b l e b y p r o v I d I g n a c o m p l e t e Mathematica风格的文档、可选的输入验证和错误策略。因此,我们相信群论概念的高级用户也将从该书和Mathematica软件包中受益。我们提供了一个紧凑的参考资料和编程环境,这将有助于以有效的方式解决实际的研究问题。
2.多级标题
在格式、样式中可以看到各种section的快捷键,alt 1 :一级标题
alt 2:二级标题

alt 7:文本
其实我不会用这个记笔记,故以上不用记
3.常用命令与快捷键
记住:
** ab (可用空格键代替)乘法 特别注意必须有空格,否则计算结果差别很多:**


在a和x之间少了一个空格,则:
 若数值算积分,乘法的这个空格更加重要!!!
若数值算积分,乘法的这个空格更加重要!!!
加;可以运算但不输出,例如: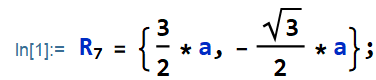 这样笔记本更好
这样笔记本更好
运行:shift+enter
内建函数首字母大写
alt 9:输入计算格式
CTRL+/ 可用于分数的输入
TAB 在各方框间移动
输入指数 (CTRL+6)、
下标 (CTRL+-) 上标:CTRL+^****
数学常数如I、E都是大写
数学输入面板会显示快捷键,但平时用数学输入面板就可以
在光标后,TranditionalForm:shift+ctrl+T
标准格式:shift+ctrl+N
注意平时不转为传统形式,因为容易看错括号(科研,很重要),还是用标准形式!!!
撤回键:

恢复:

快速选中一行或某几个:
光标在行首时按Shift+End
光标在行尾时按Shift+Home
使用shift+左右方向键可以选中其中几个。
此方法不仅适用于mma,还有思源等都能。
注释:

截图:不方便
%:前一个值
%2:前面output2 %42:前面的output42
使用假设条件:在帮助文档中输入: tutorial/AlgebraicManipulation#31833
科研中输入复杂数学公式:还是直接打公式效率最高!
可以手写,再mathpix识别,再:两种方法:但无法进行计算
1)直接粘贴就可以,不过必须加$$ $$!注意是行间公式的符号
2)ToExpression["",TeXForm]
,不过在mathpix复制后粘贴到'' ''中时间,自动会将\变成\,所以很方便!没有用,还不如第一个方法,也是无法计算。
以上两个方法都无法计算矩阵乘法。可能不是矩阵的时候也无法进行计算。
所以2.使用Windows 7 中手写的数学识别—Wolfram Mathematica 9 Documentation进行直接手写输入,输入的公式可以计算(包括矩阵乘法),但还是很慢,因为识别很不准确,特别是上下角标,所以效率很低,还不如直接打公式。
但或者直接手写,加入mathmatica后再改!而不是在数学面板中改。但识别起来还是各种错误,还不如直接打公式****
综上,mathematica中输入公式效率最高的还是直接打公式。
折叠单元:
鼠标左键双击:

删除单元:
使用delete键。 多选单元:使用shift
重要:获得向量元素就是:
C[[1, 1]]:获得C向量的第一个元素。特别注意,不能用C[1],结果不对。只有按照获得矩阵元素的方法来获得向量!故是C((20210728153817-s12x5ww '解析引用锚文本失败,请尝试更新该引用指向的定义块后再重新打开该文档'))
见“"获得矩阵元素:"[1]”(点击跳转)
矩阵与线性代数:
还是见帮助文档。
用大括号括起来的就是向量!因为在帮助文档中:

获得矩阵元素:


Wolfram 语言用列表的列表表示矩阵:
| In[1]:= | 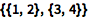
{{1, 2}, {3, 4}}
输入一个表格,用 CTRL+ ENTER 输入行,用 CTRL+ , 输入列:
| In[2]:= | 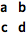
{ {a, b}, {c, d} }
| Out[2]= |  |
|---|
MatrixForm 将输出显示为一个矩阵:
| In[3]:= | 
MatrixForm[{{a, b}, {c, d}}]
| Out[3]= |  |
|---|
可以用迭代函数构建矩阵:
| In[1]:= | 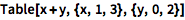
Table[x + y, {x, 1, 3}, {y, 0, 2}]
| Out[1]= |  |
|---|
或导入表示矩阵的数据:
| In[2]:= | 
Import["data.csv"]
| Out[2]= |  |
|---|
IdentityMatrix、DiagonalMatrix 和其他类似命令为内置符号.
标准的矩阵运算对元素进行操作:
| In[1]:= | 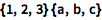
{1, 2, 3} {a, b, c}
| Out[1]= |
|---|
计算两个矩阵的点积:
| In[2]:= | 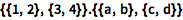
{{1, 2}, {3, 4}}.{{a, b}, {c, d}}
| Out[2]= |  |
|---|
求行列式:
| In[3]:= | 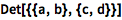
Det[{{a, b}, {c, d}}]
| Out[3]= |  |
|---|
获取矩阵的逆:
| In[4]:= | 
Inverse[{{1, 1}, {0, 1}}]
| Out[4]= |  |
|---|
用 LinearSolve 求解线性系统:
| In[1]:= | 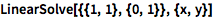
LinearSolve[{{1, 1}, {0, 1}}, {x, y}]
| Out[1]= |  |
|---|
如何用mathematica表示向量
{a1,a2,...,an}表示由a1,a2,...,an 组成的向量(注意:必须用大括号)
下列命令可以生成特殊的向量:
Table[f,{n}]生成由n个f组成的向量{f,f,f,...,f}
Table[f[n],{n,nmax}]n从1到nmax,间隔为1,生成向量{f[1], f[2], f[3],…, f[nmax]}
Table[f[n],{n,nmin, nmax}]n从nmin到nmax,间隔为1,生成向量{f[nmin], f[nmin+1],
f[nmin+2],…, f[nmax]}
Table[f[n],{n,nmin, nmax, dn}]n从nmin到nmax,间隔为dn,生成向量{f[nmin],
f[nmin+dn], f[nmin+2dn],…, f[nmax]}
如何用mathematica进行向量的加减运算及数乘运算
A+B向量A与B的和
A-B向量A与B的差
kA 或 A*k数k与向量A的数乘
如何用mathematica求向量的点积
Dot[a,b] 或a.b求向量a与b的点积(在直角坐标系中)
DotProduct[a,b]
在当前坐标系中求向量a与b的点积。在使用前,首先要加载CalculusVectorAnalysis函数库。加载方法为:
<<CalculusVectorAnalysis
加载后默认的坐标系是直角坐标系,可以根据需要设置坐标系,设置方法为:
SetCoordinates[Cartesian] (直角坐标系)
SetCoordinates[Cylindrical] (圆柱坐标系)
SetCoordinates[Spherical] (球面坐标系)
DotProduct[a,b,Cartesian]
在直角坐标系中求向量a与b的点积。在使用前,首先要加载CalculusVectorAnalysis函数库。加载方法为:
<<CalculusVectorAnalysis
若把Cartesian换为Cylindrical 或Spherical,则表示在圆柱坐标系或球面坐标系中求向量a与b的点积
如何用mathematica求向量的叉积
Cross[a, b]计算向量a与b的叉积(在直角坐标系中)
CrossProduct[a,b]
在当前坐标系中求向量a与b的叉积。在使用前,首先要加载CalculusVectorAnalysis函数库。加载方法为:
<<CalculusVectorAnalysis
加载后默认的坐标系是直角坐标系,可以根据需要设置坐标系,设置方法为:
SetCoordinates[Cartesian] (直角坐标系)
SetCoordinates[Cylindrical] (圆柱坐标系)
SetCoordinates[Spherical] (球面坐标系)
CrossProduct[a,b,Cartesian]
在直角坐标系中求向量a与b的叉积。在使用前,首先要加载CalculusVectorAnalysis函数库。加载方法为:
<<CalculusVectorAnalysis
若把Cartesian换为Cylindrical 或Spherical,则表示在圆柱坐标系或球面坐标系中求向量a与b的叉积
如何用mathematica求向量的模与夹角
Mathematica 4没有提供专门的命令求向量的模,但Mathematica 5 却提供了专门的命令求向量的模。其格式如下:
Norm[v]计算向量v的模
mathematica没有提供求两个向量夹角的命令。不过根据向量的夹角公式我们可以自己编写一个函数进行计算。
如何用mathematica建立矩阵
{{a11,a12,…,a1n},{a21,a22,…,a2n},…,{am1,am2,…amn}}建立m×n矩阵,其中aij为矩阵第i行的第j个元素(这种方法建立的矩阵不是手写的形式)
DiagonalMatrix[{a1,a2,...,an}]建立以a1,a2,...,an为对角线元素的对角矩阵(这种方法建立的矩阵不是手写的形式)
IdentityMatrix[n]生成一个n×n单位矩阵(这种方法建立的矩阵不是手写的形式)
Table[f,{i,m},{j,n}]生成m×n矩阵(这种方法建立的矩阵不是手写的形式)
Array[a,{m,n}]生成以am×n为元素的矩阵(这种方法建立的矩阵不是手写的形式)
MatrixForm[A]矩阵A的手写形式
如何用mathematica求行列式的值
Det[A]求矩阵A的行列式
如何用mathematica求逆矩阵
Inverse[A]求矩阵A的逆矩阵
如何用mathematica求转置矩阵
Transpose[A]求矩阵A的转置矩阵
如何用mathematica求矩阵的秩
mathematica 4没有提供这一命令,但mathematica 5 提供了这一命令,格式如下:
MatrixRank[A]求矩阵A的秩
如何用Mathematica求矩阵的迹
Tr[A]求方阵A的迹
如何用mathematica求特征值和特征向量
Eigenvalues[A]求矩阵A的所有特征值
Eigenvectors[A]求矩阵A的所有特征向量
Eigensystem[A]求矩阵A的所有特征值和特征向量,输出格式为{特征值,特征向量}
如何用mathematica解线性方程组
Solve[{eqn1,eqn2,…},{x,y,z,…}]解由方程eqn1,eqn2,…组成的方程组。
LinearSolve[M,B]解满足矩阵方程MX=B的向量X
复共轭:

解久期行列式可以转化为求矩阵特征值和特征向量:

但这只对都是数值的矩阵有效。对于含参数变量的矩阵,Eigenvalues这个命令无效
变量替换:
表达式/.x->a 表达式/.{x->a, y->b,…}
必须用完全化简!!!:我遇到过这个问题,花了很长时间,以为自己算错了,其实没算错,只要用fullsimplify就能完全化简,得到的结果就和论文一致
对于科研中out1这样的复杂公式:
使用化简或因式分解都是不能得到和论文中的一样的结果,只有用fullsimplify完全化简的结果才和论文中的结果一样,所以以后必须只用fullsimplify完全化简!!!

(最后这个out9的结果才和论文中的一致)
在假设条件下化简表达式:

不过注意,在假设条件中使用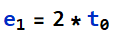 这样的公式后,
这样的公式后,

之后即使我删去97这个单元块以后,因为已经使用过赋值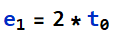 ,故即使删去97这个单元块以后,在后面的计算中,也会自动将\(e_1\)替换为\(2t_0\),这样会造成问题!(因为前面97这个单元块只是我想试一下若
,故即使删去97这个单元块以后,在后面的计算中,也会自动将\(e_1\)替换为\(2t_0\),这样会造成问题!(因为前面97这个单元块只是我想试一下若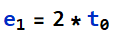 结果会等于什么,并不是后面一直都用
结果会等于什么,并不是后面一直都用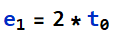 )
)
清除赋值:
对于上面出现的赋值的问题: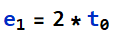 。唯一的清除这种符号的赋值的方法是:
。唯一的清除这种符号的赋值的方法是:
而不能用 (此语法是清除数值的赋值)。
(此语法是清除数值的赋值)。

则: ,故确实清除了赋值!
,故确实清除了赋值!
mathematica 中为变量的赋值时永久性的。
为避免程序的程序错误和节省资源,mathematica 中用完一个变量后就应该马上清除他。
有两种个别地清除变量值的方法:
var=.Clear[var]
PS: 如果要清除函数,只有第二种方法会有效果。而清除带下标的变量,只有第一种方法有效果。
清除全部变量:以后在所有文档的开头都写:Remove["`*"]; (特别是在“备份、其他”这个文档中经常用)
但是很奇怪的是,这个命令只能清除这种变量:
对于带下标的量,无法清除:
,将t0写成输入格式也不行。确实,这就是mathematica的bug.
帮助文档中没有提示会有这个bug,所以帮助文档不好,浪费我时间。
以后在所有文档的开头都写:Remove["`*"]; 来源:Mathematica消除所有变量_SCI守望者的博客-CSDN博客
0.解释:Remove[]函数的作用就是消除变量,使用此函数后变量的定义将被删除。与之类似的是mathematica中的Clear[]函数,但是Clear["`*"]函数只能消除变量的赋值,变量(的定义)还是存在的。
1.Mathematica软件刚启动的时候,是没有变量驻扎内存的,那清除所有变量有何意义?
答:建议在程序开头写Remove["`*"]的原因:要养成清除变量的好习惯,
当你的代码有清除变量的时候,
别人拿到你的代码的时候,可能之前有变量,有可能存在冲突,
所以清除掉。2.不用帮助文档说的Clear["Global`*"]的原因:(帮助文档这里确实乱说,还说它能清除所有,其实并不能)
见https://zhidao.baidu.com/question/514950375.html,其中说了:Clear["Clobal`*"]清除不了带下标的变量及其值,因为:
(其中说的Clear[Subscript]就是清除所有与Subscript相关的定义。这样一来,就导致任何带下标的定义都能被清除了。但这个方法只针对代下标的变量,所以还是用Remove["`*"])
3.注意,若已经去除了,什么都没有的情况下,若使用Remove["`*"],则会出现错误:
(18这个remove成功了,而119这个remove出现错误,这是因为118这个remove已经去除了东西,而119这个remove就没有用,会出现错误。)
复数、三角函数表达式的相关化简:
将表达式展开为 a+Ib 形式
ComplexExpand[表达式] **将表达式展开为 a+Ib 形式**,默认所有的变量都是实数<br /> ComplexExpand[表达式,{x,y,…}] **将表达式展开为 a+Ib 的形式**,假设x,y,…等变量都是复数
TrigExpand[表达式] 将三角函数展开
TrigFactor[表达式] 将三角函数组成的表达式因式分解
TrigReduce[表达式] 将相乘或乘方的三角函数化成一次方的基本组合
ExpToTrig[表达式] 将指数函数化成三角函数或双曲函数
TrigToExp[表达式] 将三角函数或双曲函数化成指数函数
^a+b*I表示复数a+bI
Conjugate[z]求复数z的共轭复数
Exp[z]复数的指数函数,表示e^z
Re[z]求复数z的实部
Im[z]求复数z的虚部
合并同类项
Collect[表达式,指定的变量]
因式分解
Factor[表达式]
do、while、for循环:

定义函数:
从帮助文档中学,或https://www.wolfram.com/language/fast-introduction-for-programmers/zh/notebook-documents/
4.重要:Mathematica 记笔记、制作笔记本:
一个笔记本中不可以分单元独立运行,只能全局运行,我查了。所以只能新开一个笔记本。
帮助文档可以分单元独立运行,是因为帮助文档有额外的底层复杂程序,复杂,算了
样式(使用快捷键)和样式表,就能实现普通笔记本:

记笔记:
当输入普通文字笔记时,用alt+7写text,当输入计算单元时,用alt+9。当输入标题时,用:

当输入公式时,用:

当输入无序列表时,用:
5.函数式编程,科研
函数式编程,定义函数,重复操作用Do循环等内容见帮助文档:tutorial/FunctionsAndPrograms#13037
写得好!!!



6.重要:特殊值法:给未知量取试探值的方法!
比如t1不知道,但我们可以取t1的试探值,从而可以知道三个表达式的大小关系,在科研中确实有用,而且可以写数值程序(本来我的思路是符号计算的程序,但可以利用此方法,写数值计算程序,更好,因为mma不一定符号计算能算出来)
7.较少用到的命令:
一些标记:


复原:
 (mathematica好像不能回退笔记本历史,只有复原这个功能,但容易现在的数据就没了,所以使用mathematica中必须注意保存和备份!!!)
(mathematica好像不能回退笔记本历史,只有复原这个功能,但容易现在的数据就没了,所以使用mathematica中必须注意保存和备份!!!)
如何用Mathematica展开
Expand[表达式]
如何用Mathematica进行化简
Simplify[表达式]
Simplify[表达式,假设条件]
FullSimplify[表达式]
FullSimplify[表达式,假设条件]
8.科研中mathematica的注意事项
1)使用simplify时的问题:影响整个笔记本
见:"必须用完全化简!!!:我遇到过这个问题,花了很长时间,以为自己算错了,其实没算错,只要用fullsimplify就能完全化简,得..."[2]
解决方法:“"清除赋值:"[3]”
2)使用mathematica过程中,经常记得备份文档,因为不能从笔记历史记录还原
在"mathematica 所有文档”这个文件夹中有一个“备份、其他”文档,就是临时记一些东西
3)科研,非常重要:当有不精确小数时,加号和乘号一起运算时,加号必须加空格,否则算错
科研中发现的问题:

以上第55个式子才是正确的。第54个式子算出来的结果是错误的。它们的差别仅仅是+号右边是否有空格!!!
!!!所以记住,为了保险,平时科研时,加号和乘号一起运算时,加号必须加空格,否则算错
后来mathematica团队说,这个问题是因为and +会相互作用,导致这个问题,所以当有and +时必须有空格。他们说以后会修正这个问题。
4)科研中解方程组时Solve遇到的问题:当方程中的系数等都是很复杂的小数时,此方程组无法用solve得到自洽的精确的解!此时只有自己在纸上解方程组!!!

a.output解集为空的原因是:这些方程中的系数等都是很复杂的小数,所以这个方程组无法用solve得到自洽的精确的解!此时只有自己在纸上解方程组!!!
b.提示信息:“Solve::ratnz: Solve 无法求解具有不精确系数的系统. 答案是通过求解相应的精确系统并且将结果数值化处理得到的.”的含义为:从其他地方复制来的1.59845等量都是不精确的小数,但其实它依然进行了求解并得到了答案为空集。故此提示信息不用管。
5)重要:下标问题。解决方法:使用notation包和symbolize构成复合结构
这样的两个下标(一个为数字一个为字母)居然无法给变量命名:
 ,在运行后,若输入:
,在运行后,若输入: (以前一直都没出现过kx这个量),即k1x无法给变量命名,没出现过的kx居然有的是k1x的值!所以mathematica的下标问题很严重。
(以前一直都没出现过kx这个量),即k1x无法给变量命名,没出现过的kx居然有的是k1x的值!所以mathematica的下标问题很严重。
但是当下标为1个变量或下标为两个数字或下标为两个字母时,可以给下标命名,不会出现问题:

以后在所有文档开头加上这两行命令,就不会再有下标问题:

 (此时就没有下标问题了)
(此时就没有下标问题了)
若需要用到上标来给变量命名,则只好自己使用symbolize,例如:
 (从而此符号不会再有问题)
(从而此符号不会再有问题)
notation包中还有一些功能,可以实现自定义符号复合结构及替换等功能,帮助文档写得很好。
6)公式复杂到了一定程度时(比如有根号又20多行),mma就很多bug,不能用,故对太复杂符号计算,不能用mma!
2013 三能带紧束缚模型的最近邻情况的参数求解中:


9.常用命令 版本2 2014物理和工程中的数学
注意可以球坐标和直角坐标及其表达式之间转换。
可以取转置共轭
还有张量分析


MATHEMATICA LANGUAGE SUMMARY
Commands that are underlined are not part of the basic language: code for them is given in this book. Some Basics:
Arithmetic operations: a+b, a-b, a*b, a/b,a~b (a>),
Logical/relational: allb,a&&b,!a,(or,and,not); a>b,a>=b,a<b,a<=b,a==b,a!=b(a≠b), String: "string",Assignment: a = expr,Comment:(* comment *),
Command ending (print)(none)(do not print); FindRoot[eqn,{x,xO}(get root near x0), Force evaluation: Evaluate[expr], Floating-point evaluation: N[expr], Undefine x: Clear[x]. Simplify or Transform:
Simplify[exprl, Together[exprl, Factor[expr], FactorTerms[expr], Expand[exprl, Collect[expr,x],Apart [expr] (converts to partial fractions),
TrigToExp[expr](https://assets.b3logfile.com/siyuan/1619246215189/converts circular/hyperbolic trig functions to exponential form), ExpToTrig[expr](https://assets.b3logfile.com/siyuan/1619246215189/converts exponentials to circular/hyperbolic trig form),
Round[x](https://assets.b3logfile.com/siyuan/1619246215189/round x to nearest integer), Coefficient[polynomial,x^n](https://assets.b3logfile.com/siyuan/1619246215189/coefficient of x), FunctionExpand [expr](https://assets.b3logfile.com/siyuan/1619246215189/tries to evaluate special functions).
Substitution: expr /.x=value(returns expr with x set to value, stored exrpr unchanged).
Programming:
Do [statement;·.; statement,{n,n1,n2}],
If [condition, then-statement;.·;then-statement,else-statement;·;else-statement], While [condition, statement;.··; statement],
procname[args_] := Module[{local variables,bodgl,
Break,Continue.
Const ants:
I,Pi,E,True,False,Infinity,EulerGamma(Euler-Mascheroni constant), Catalan.
Elementary Functions and Coefficients:
Sign[x],
BernoulliB[n],
n!,dfac [n] =n!,Binomial[n,m] =(m), Sqrt [x], Abs [x], Exp[x]=e*x, Log[x], Sin[x], Sinh [x],
ArcSin [x],ArcSinh [x].
In all four of the above Sin can be replaced by Cos, Tan, Cot,Sec,or Csc.
Special Functions:
Gamma[s], Gamma[s,x](https://assets.b3logfile.com/siyuan/1619246215189/integral x to o), Beta[p,q],
Erf[x], Erfc[x],
PolyGamma[n,s]= y(n)(s),ExpIntegralE[n,x]=E, (c),
PolyGamma[s]= vp(s),
ExpIntegralEi[x],Zeta[s], BesselJ[n,x], BesselY[n,x]), BesselI[n,x],BesselK[n,x], BesselJZero[n,j], BesselYZero[n,j], HankelH1[n,x],HankelH2[n,x], SphericalBesselJ[n,x], SphericalBesselY[n,x],SphericalBesselI[n,x], SphericalBesselK[n,x], SphericalHankelH1[n,x], SphericalHankelH2[n,x], SphericalHarmonicY[L,M,theta,phi].
Orthogonal Polynomials:HermiteH[n,x],
LegendreP[n,x],LegendreQ[n,x],LegendreP [n,m,x], LaguerreL[n,x],LaguerreL[n,k,x],ChebyshevT[n,x].
Complex Variables:
I, Re[z],Im[z], Conjugate[z],Abs[z],Arg[z], Residue[expr,{z,z0}], ComplexExpand[z](https://assets.b3logfile.com/siyuan/1619246215189/attempts to find real and imaginary parts)
Sums, Integrals, Limits, Derivatives:
Sum[eapr(m),{m,n1,n2}], Integrate[expr(c),{x,x1,x2}],Limit[eapr,x -> x0], Series[expr, fx, a,n}](https://assets.b3logfile.com/siyuan/1619246215189/expansion about a, which can be Infinity; approximately n terms), Normal[series](https://assets.b3logfile.com/siyuan/1619246215189/converts from series form to ordinary expression), D[eapr(a),x],D[expr(&,y), x,y], D[expr(a),x,x]Linear Algebra:
V = {v1,v2,}(vector,row or column),V[[i]](https://assets.b3logfile.com/siyuan/1619246215189/ith element of V),V1.V2 (dot product), M = ffrou},{rou},…}(matrix),M[[i]](https://assets.b3logfile.com/siyuan/1619246215189/ith row of M), Part[M,All,j](https://assets.b3logfile.com/siyuan/1619246215189/jth column of M), M[[i,j]] (element(i,/) of M),M.M,M.V,V.M valid, Transpose[M],ConjugateTranspose[M], If Eq1 = a11x1+a12x2 == b1 etc,Solve[{Eq1,Eq2,},{x1,x2,}](https://assets.b3logfile.com/siyuan/1619246215189/solves equation system), Inverse【M】, SProd【F(θ,g),G(0,o)】(angular scalar product in spherical coordinates),Det[M],TrM,Orthogonalize[M](https://assets.b3logfile.com/siyuan/1619246215189/vectors are rows of M),Val := Eigenvalues [M],
Vec:= Eigenvectors [M],{Val,Vec}= Eigensystem[M] (eigenvalues in Val, vectors as rows in Vec).
Vector Analysis:
A. B, CroSs [A,B], After <<VectorAnalysis':
SetCoordinates[Cartesian[x,y,z]]or Spherical or Cylindrical to establish coordinates,then Grad[expr(a,y,z)], Div([vector], Curl[vector],Laplacian[expr(a,y,z)],Laplacian[vector], CoordinatesFromCartesian[V,coords] (converts from Cartesian to coords), CoordinatesToCartesian[V,coords](https://assets.b3logfile.com/siyuan/1619246215189/converts to Cartesian from coords).
Tensor Analysis:
T := Array(1..3,1..3,1..3,nested list)(build tensor),MatrixForm(T)(view elements), Transpose[tensor,{new index: order}]
T1.T2 (contract last index of T1 with first of T2), Tr[T,plus,2](https://assets.b3logfile.com/siyuan/1619246215189/contract first two indices of T), KroneckerDelta[i,j], Signature[i,j,k](https://assets.b3logfile.com/siyuan/1619246215189/Levi-Civita symbol).
Solving Differential Equations:
ODE = F(diff(y(x),x,x),diff(y(x),x),y(x))== g(x), dsolve({ODE,conditions)(conditions are equations,e.g., y(0)==0).
Integral Transforms:
FourierTransform[expr,t,w],FourierSinTransform[expr,t,v],FourierCosTransform[expr,t,w], InverseFourierTransform[expr,w,t],HeavisideTheta[t],DiracDelta[t], LaplaceTransform[expr,t,s],InverseLaplaceTransform[evpr,s,t].
Probability: BinomialB[n,s,pl,PoissonP[n,nu],GaussG[mu,sigma,x],GaussPhi[mu,sigma,x]. Curve Fitting, Least Squares:
data ={ fx1,y1},{x2,y2},…} or data = Table[{n,F[n]},{n,n1,n2}], Fit[data,{1, V,·..},v].
Making Tables and Plots: See Appendices A and B.
Mathematica 10.3与数字化大学物理
江俊勤
Year:
2019
Edition:
1
Publisher:
科学出版社
Mathematica的内部常数
Pi , 或 π(从基本输入工具栏输入, 或“Esc”+“p”+“Esc”)圆周率 π<br /> E (从基本输入工具栏输入, 或“Esc”+“ee”+“Esc”)自然对数的底数e<br /> I (从基本输入工具栏输入, 或“Esc”+“ii”+“Esc”)虚数单位i<br /> Infinity, 或 ∞(从基本输入工具栏输入 , 或“Esc”+“inf”+“Esc”)无穷大 ∞<br /> Degree 或°(从基本输入工具栏输入,或“Esc”+“deg”+“Esc”)度<br />Mathematica的常用内部数学函数 <br /> 指数函数Exp[x]以e为底数<br /> 对数函数Log[x]自然对数,即以e为底数的对数<br /> Log[a,x]以a为底数的x的对数<br /> 开方函数Sqrt[x]表示x的算术平方根<br /> 绝对值函数Abs[x]表示x的绝对值<br /> 三角函数<br /> (自变量的单位为弧度)Sin[x]正弦函数<br /> Cos[x]余弦函数<br /> Tan[x]正切函数<br /> Cot[x]余切函数<br /> Sec[x]正割函数<br /> Csc[x]余割函数<br /> 反三角函数ArcSin[x]反正弦函数<br /> ArcCos[x]反余弦函数<br /> ArcTan[x]反正切函数<br /> ArcCot[x]反余切函数<br /> ArcSec[x]反正割函数<br /> ArcCsc[x]反余割函数<br /> 双曲函数Sinh[x]双曲正弦函数<br /> Cosh[x]双曲余弦函数<br /> Tanh[x]双曲正切函数<br /> Coth[x]双曲余切函数<br /> Sech[x]双曲正割函数<br /> Csch[x]双曲余割函数<br /> 反双曲函数ArcSinh[x]反双曲正弦函数<br /> ArcCosh[x]反双曲余弦函数<br /> ArcTanh[x]反双曲正切函数<br /> ArcCoth[x]反双曲余切函数<br /> ArcSech[x]反双曲正割函数<br /> ArcCsch[x]反双曲余割函数<br /> 求角度函数ArcTan[x,y]以坐标原点为顶点,x轴正半轴为始边,从原点到点(x,y)的射线为终边的角,其单位为弧度<br /># 数学排版显示<br />
数论函数
GCD[a,b,c,...]最大公约数函数
LCM[a,b,c,...]最小公倍数函数
Mod[m,n]求余函数(表示m除以n的余数)
Quotient[m,n]求商函数(表示m除以n的商)
Divisors[n]求所有可以整除n的整数
FactorInteger[n]因数分解,即把整数分解成质数的乘积
Prime[n]求第n个质数
PrimeQ[n]判断整数n是否为质数,若是,则结果为True,否则结果为False
Random[Integer,{m,n}]随机产生m到n之间的整数
排列组合函数Factorial[n]或n!阶乘函数,表示n的阶乘
复数函数Re[z]实部函数
Im[z]虚部函数
Arg(z)辐角函数
Abs[z]求复数的模
Conjugate[z]求复数的共轭复数
Exp[z]复数指数函数
求整函数与截尾函数Ceiling[x]表示大于或等于实数x的最小整数
Floor[x]表示小于或等于实数x的最大整数
Round[x]表示最接近x的整数
IntegerPart[x]表示实数x的整数部分
FractionalPart[x]表示实数x的小数部分
分数与浮点数运算函数N[num]或num//N把精确数num化成浮点数(默认16位有效数字)
N[num,n]把精确数num化成具有n个有效数字的浮点数
NumberForm[num,n]以n个有效数字表示num
Rationalize[float]将浮点数float转换成与其相等的分数
Rationalize[float,dx]将浮点数float转换成与其近似相等的分数,误差小于dx
最大、最小函数Max[a,b,c,...]求最大数
Min[a,b,c,...]求最小数
符号函数Sign[x]
Mathematica中的数学运算符
a+b 加法
a-b减法
ab (可用空格键代替)乘法
a/b (输入方法为:“ Ctrl ” + “ / ” ) 除法
a^b (输入方法为:“ Ctrl ” + “ ^ ” )乘方
-a 负号
Mathematica的关系运算符
==等于
<小于
>大于
<=小于或等于
>=大于或等于
!=不等于
注:上面的关系运算符也可从基本输入工具栏输入。
如何用mathematica求多项式的最大公因式和最小公倍式
PolynomialGCD[p1,p2,...]求多项式p1,p2,...的最大公因式
PolynomialLCM[p1,p2,...]求多项式p1,p2,...的最小公倍式
如何用mathematica求整数的最大公约数和最小公倍数
GCD[p1,p2,...]求整数p1,p2,...的最大公约数
LCM[p1,p2,...]求整数p1,p2,...的最小公倍数
如何用mathematica进行整数的质因数分解
FactorInteger[n]把整数n分解成质数的乘积
如何用mathematica求整数的正约数
Divisors[n]求整数n的所有正约数
如何用mathematica判断一个整数是否为质数
PrimeQ[n]判断整数n是否为质数,若是,则运算结果为True,否则结果为False
如何用mathematica求第n个质数
Prime[n]求第n个质数
如何用mathematica求阶乘
Factorial[n]或n!求n的阶乘
如何用mathematica配方
Mathematica没有提供专门的配方命令,但是我们可以非常轻松地自定义一个函数进行配方。
如何用mathematica进行多项式运算
Collect[expr,x]将expr表示成x的多项式
Collect[expr,x,func]将expr表示成x的多项式之后,再根据func处理各项系数
Collect[expr,{x,y}]将expr表示成x的多项式,再把多项式的每一项系数表示成y的多项式
FactorTerms[expr]提出expr中的数值因子
FactorTerms[expr,x]提出expr中所有不包含x的因子
FactorTerms[expr,{x,y,...}]提出expr中所有不包含x,y,...的因子
PolynomialGCD[p1,p2,...]求多项式p1,p2,...的最大公因式
PolynomialLCM[p1,p2,...]求多项式p1,p2,...的最小公倍式
PolynomialQuotient[p1,p2,x]变量为x,求p1/p2 的商
PolynomialRemainder[p1,p2,x]变量为x,求p1/p2 的余式
PowerExpand[expr]将(xy)n分解成 xnyn 的形式
如何用mathematica进行分式运算
Denominator[f]提取分式f的分母
Numerator[f]提取分式f的分子
ExpandDenominator[f]展开分式f的分母
ExpandNumerator[f]展开分式f的分子
Expand[f]把分式f的分子展开,分母不变且被看成单项。
ExpandAll[f]把分式f的分母和分子全部展开
ExpandAll[f, x]只展开分式f中与x匹配的项
Together[f]把分式f的各项通分后再合并成一项
Apart[f]把分式f拆分成多个分式的和的形式
Apart[f, x]对指定的变量x(x以外的变量作为常数),把分式f拆分成多个分式的和的形式
Cancel[f]把分式f的分子和分母约分
Factor[f]把分式f的分母和分子因式分解
** **
如何用mathematica进行复数运算
a+bI表示复数a+bI
Conjugate[z]求复数z的共轭复数
Exp[z]复数的指数函数,表示e^z
Re[z]求复数z的实部
Im[z]求复数z的虚部
Abs[z]求复数z的模
Arg[z]求复数z的辐角,
如何在mathematica中表示集合
与数学中表示集合的方法相同,格式如下:
{a, b, c,…}表示由a, b, c,…组成的集合 (注意:必须用大括号)
下列命令可以生成特殊的集合:
Table[f,{n}]生成包含n个元素f的集合
Table[f[n],{n,nmax}]n从1到nmax,间隔为1,生成集合{f[1], f[2], f[3],…, f[nmax]}
Table[f[n],{n,nmin, nmax}]n从nmin到nmax,间隔为1,生成集合{f[nmin], f[nmin+1],
f[nmin+2],…, f[nmax]}
Table[f[n],{n,nmin, nmax, dn}]n从nmin到nmax,间隔为dn,生成集合{f[nmin],
f[nmin+dn], f[nmin+2dn],…, f[nmax]}
Range[n]生成集合{1, 2, 3 ,…, n}
Range[imin, imax]生成集合{imin,imin+1,imin+2,…,imax}
Range[imin, imax, di]生成集合{imin,imin+di,imin+2*di,… } (最大不超过imax)
如何用Mathematica求集合的交集、并集、差集和补集
Union[A,B,C,…] 求集合A,B,C,…的并集
AUnionBUnionCUnion… 求集合A,B,C,…的并集
A∪B∪C∪… 求集合A,B,C,…的并集
Intersection[A,B,C,…] 求集合A,B,C,…的交集
A~ Intersection B Intersection C Intersection ~… 求集合A,B,C,…的交集
A∩B∩C∩… 求集合A,B,C,…的交集
Complement [A,B,C,…] 求差集
A~ Complement B Complement C Complement ~… 求差集
Complement [全集I,A] 求集合A关于全集I的补集
全集I ~ Complement ~A 求集合A关于全集I的补集
如何mathematica用排序
Sort[v]将数组或向量v的元素从小到大排列(升序排列)
Reverse[v]将数组或向量v的元素按照与原来相反的顺序重新排列(续排列)
RotateLeft[v]将数组或向量v中的每一个元素向左移一个位置
RotateRight[v]将数组或向量v中的每一个元素向右移一个位置
RotateLeft[v,n]将数组或向量v中的每一个元素向左移n个位置
RotateRight[v,n]将数组或向量v中的每一个元素向右移n个位置
如何在Mathematica中解方程
Solve[方程,变元]
注:方程的等号必须用: = =
如何在Mathematica中解方程组
Solve[{方程组},{变元组}]
注:方程的等号必须用: = =
如何在Mathematica中解不等式
先加载:AlgebraInequalitySolve ,加载方法为:<<AlgebraInequalitySolve
然后执行解不等式的命令InequalitySolve,此命令的使用格式如下:
<--mstheme-->
<--mstheme-->
InequalitySolve[不等式,变元]
<--mstheme-->
如何在Mathematica中解不等式组
先加载:AlgebraInequalitySolve ,加载方法为:<<AlgebraInequalitySolve
然后执行解不等式组的命令InequalitySolve,此命令的使用格式如下:
<--mstheme-->
<--mstheme-->
InequalitySolve[{不等式组},{变元组}] (我的研究成果)
InequalitySolve[And[不等式组],{变元组}]
InequalitySolve[不等式1&&不等式2&&…&&不等式n,{变元组}]
<--mstheme-->
如何在Mathematica中解不等式组
先加载:AlgebraInequalitySolve ,加载方法为:<<AlgebraInequalitySolve
然后执行解不等式组的命令InequalitySolve,此命令的使用格式如下:
<--mstheme-->
<--mstheme-->
InequalitySolve[{不等式组},{变元组}] (我的研究成果)
InequalitySolve[And[不等式组],{变元组}]
InequalitySolve[不等式1&&不等式2&&…&&不等式n,{变元组}]
如何用mathematica表示分段函数
lhs:=rhs/;condition当condition成立时,lhs才会被定义成rhs
If[test,then,else]如果test为True,则执行then,否则执行 else
If[test,then,else,unknown]如果test为True,则执行then,为False时,则执行
else,无法判断test是True或False时则执行unknown
Which[test1,value1,test2,value2,...]如果test1为True,则执行value1,test2为True,则执行value2,依次类推。
如何用mathematica求反函数
InverseFunction[f]求f的反函数
对系统内部的函数生效,但对自定义的函数不起任何作用,也许是方法不对。
如何用Mathematica画图
<--mstheme-->
Plot[表达式,{变量,下限,上限},可选项]
如何用mathematica绘制2D隐函数图象
首先要加载GraphicsImplicitPlot函数库,加载方法为:<<GraphicsImplicitPlot
ImplicitPlot[eqn,{x,xmin,xmax}]先用Solve命令求解,再在指定的范围内绘制隐函数图形。
ImplicitPlot[eqn,{x, xmin, m1, m2, …, xmax}]避开m1, m2, …点绘图
ImplicitPlot[eqn,{x,xmin,xmax},{y, ymin , ymax}]用ContourPlot的方法绘图
ImplicitPlot[{eqn1,eqn2,…}, ranges, options]同时绘制多个隐函数图
如何用mathematica进行2D参数绘图
ParametricPlot [{x(t), y(t)},{t, tmin, tmax}]绘制二维曲线的参数图
ParametricPlot [{x(t), y(t)},{t, tmin,
tmax},AspectRatio->Automatic]绘制二维曲线的参数图,并保持曲线的“真正形状”,即x,y坐标的比为1:1
ParametricPlot [{{x1(t), y1(t)}, {x2(t), y2(t)},…}, {t, tmin,
tmax}]同时绘制多个参数图
如何用mathematica进行极坐标绘图
首先要加载GraphicsGraphics函数库,加载方法为:<< GraphicsGraphics
PolarPlot[r(θ),{θ,θ1,θ2}]在极坐标系中绘制r=r(θ)的图形,角度θ从θ1到θ2
PolarPlot[{r1(θ), r2(θ),…},{θ,θ1,θ2}]在同一个极坐标系中同时绘制多个图形
如何用mathematica绘制二维散点图
ListPlot[{y1,y2,y3,…}]在二维平面上绘点{1,y1},{2,y2},…
ListPlot[{{x1, y1},{x2, y2},{x3, y3},…}]在二维平面上绘点{x1,y1},{x2,y2},…
ListPlot[list,PlotJoined->True]用线段连接绘制的点,其中list为数据点
Mathematica的2D绘图选项
选项必须放在最后面,其格式为:option->value
选 项默 认 值说 明
AspectRatio1/GoldenRatio图形高与宽的比例。默认值为1/GoldenRatio,约为0.618
AxesTrue是否绘制出坐标轴,设False,则不绘制任何坐标轴。设Axes->{False,True},则只绘制出y轴
AxesLabelAutomatic为坐标轴做标记,设AxesLabel->{“ylabel”},则为y轴做标记。设AxesLabel->{“xlabel”
,“ylabel”},则为{x, y}轴做标记。
AxesOriginAutomaticAxesOrigin->{x,y},设坐标轴相交点为{x,y}
DisplayFunction\(DisplayFunction定义图形的显示。设Identity将不显示任何图形<br /> FrameFalse是否给图形加上外框<br /> FrameLabelFalse从x轴下方顺时针方向给图形加上外框标记<br /> FrameLabel->None定义无外框标记<br /> FrameLabel->{x,y}定义图形下方与左边的标记<br /> FrameLabel->{x1, y1 , x2, y2}从x轴下方顺时针方向,定义图形四边的标记。<br /> FrameTicksAutomatic给外框加上刻度(如果Frame设为True); None<br /> 则不加刻度。定义{xticks,yticks,…}则分别设置每一边的刻度。<br /> GridLinesNone设Automatic则在主要刻度上加上网格线。<br /> GridLines->{xgrid,ygrid}定义x与y方向的网格数。<br /> PlotLabelNonePlotLabel->label定义整个图形的名称。<br /> PlotRangeAutomatic设PlotRange->All, 绘制所有图形<br /> 设PlotRange->{min, max}, 指定y方向的绘图范围<br /> 设PlotRange->{{xmin, xmax}, {ymin,ymax}},分别指定x与y方向的绘图范围<br /> TicksAutomatic坐标轴的刻度<br /> 设Ticks->None,则不显示刻度记号<br /> 设Ticks->{xticks,yticks},定义x与y方向刻度记号的位置。<br /> 设Ticks->{{x1,label1},<br /> {x2,label2},…},在x1位置标注label1记号,在x2位置标注label2记号,…<br /> 设Ticks->{{x1,label1,len1}, {x2,label2,len2},…},定义每一个刻度的长度<br /> <br /> Automatic, None, All, True, False是Mathematica绘图命令常用的选项,它们所代表的意义如下:<br /> Automatic使用Mathematica的默认值<br /> None不包含此项<br /> All包含每项<br /> True此项有效<br /> False此项无效<br /> 下列选项可以格式化图形里的文字:<br /> TextStyle->value定义整张图形中所有文字的样式<br /> “style” 将图形文字的样式定义为cell的样式<br /> FontSize->n, 定义字体大小为n<br /> FontSlant->”Italic”, 定义字体为斜字体<br /> FontWeight->”Bold”, 定义字体为粗字体<br /> FontFamily->”name”, 定义字体,如”Times”<br /> FormatType->value定义为TraditionalForm则以标准的数学格式输出<br /> 下列选项可以定义绘图的颜色与线条的粗细:<br /> Plot[{f1,f2,…},{x,xmin,xmax},PlotStyle->{RGBColor[r1,g1,b1],<br /> RGBColor[r2,g2,b2],…}]分别用RGBColor[r1,g1,b1],<br /> RGBColor[r2,g2,b2],…给f1,f2,…上色<br /> Plot[{f1,f2,…},{x,xmin,xmax},PlotStyle->{GrayLevel,<br /> GrayLevel[j],…}]分别用GrayLevel,<br /> GrayLevel[j],…给f1,f2,…上色<br /> Plot[{f1,f2,…},{x,xmin,xmax},PlotStyle->{Thickness[r1],<br /> Thickness[r2],…}]分别用Thickness[r1],<br /> Thickness[r2],…定义f1,f2,…的粗细,其中r1,r2 为线条的粗细所占图形宽度的比例。<br /> 如何用mathematica绘制3D显函数的图形 <br /> Plot3D[f(x, y), {x, xmin, xmax}, {y, ymin, ymax}]x 从xmin到 xmax, y从<br /> ymin到 ymax,绘制函数 f(x,y)的图形<br /><br /> 如何用mathematica绘制3D隐函数图象 <br /> 首先要加载Graphics`ContourPlot3D`函数库,加载方法为:<<Graphics` ContourPlot3D `<br /> ContourPlot3D[f(x,y,z),{x, xmin, xmax},{y, ymin , ymax}, {z, zmin ,<br /> zmax}]在指定的范围内画出f(x,y,z)=0的三维立体图<br /><br /> 如何用mathematica进行3D参数绘图(空间曲线、曲面的参数绘图) <br /> ParametricPlot3D[{f(t), g(t), h(t)},{t, tmin, tmax}]绘制三维的空间曲线参数图<br /> ParametricPlot3D[{f(u,v),g(u,v),h(u,v)},{u,umin,umax},{v,vmin,vmax}]绘制三维的空间曲面参数图<br /> ParametricPlot3D[{{fx,fy,fz},{gx,gy,gz},…},…]同时绘制多个参数图<br /> ParametricPlot3D[{fx,fy,fz,s},…]根据函数s上色<br /><br /> 如何用mathematica绘制三维散点图 <br /> ScatterPlot3D[{{x1, y1, z1}, {x2, y2, z2},…}]在三维空间中绘制数据点{x1, y1,<br /> z1}, {x2, y2, z2},…<br /> 。在使用前首先要加载Graphics`Graphics3D`绘图函数库,加载方法为:<<Graphics`Graphics3D`<br /> ScatterPlot3D[{{x1,y1,z1},{x2,y2,z2},…},<br /> PlotJoined->True]在三维空间中绘制数据点{x1, y1, z1}, {x2, y2,<br /> z2},…并用线段将点连接起来。在使用前首先要加载Graphics`Graphics3D`绘图函数库,加载方法为:<<Graphics`Graphics3D`<br /><br /> mathematica的3D绘图选项 <br /> 基本格式:option->value<br /> 选 项默 认 值说 明<br /> AxesTrue是否控制坐标轴<br /> AxesLabelNone坐标轴的名称。{”xlabel”, ”ylabel”, ”zlabel”}分别为x、y、z轴的标注。<br /> BoxedTrue绘制外框。定义为False则不绘制外框<br /> ColorFunctionAutomatic上色的方式。Hue为彩色<br /> DisplayFunction\)DisplayFunction显示图形的模式。定义为Identity则不显示图形
FaceGridsNone表面网格。选All则在外框每面都加上网格
HiddenSurfaceTrue是否去掉隐藏线
LightingTrue是否用仿真光线(simulated lighting)上色
MeshTrue是否在图形表面加上网格线
PlotRangeAutomaticZ方向的绘图范围
ShadingTrue表面不上色或留白
ViewPoint{-1.3, -2.4, 2}观测点(眼睛观测的位置)
PlotPoints15在x和y方向取样点
CompiledTrue是否编译成低级的机器码
ViewPoint 可以定义从不同的角度观看三维的函数图,下表提供了一些典型值:
ViewPoint的值观测点位置
{-1.3, -2.4, 2}默认观测点
{0,-2,0}从前方看
{0,0,2}从上往下看
{0,-2,2}从前方上面往下看
{0,-2,-2}从前方下面往上看
{-2,-2,0}从左前方看
{2,-2,0}从右前方看
如果设Lighting为False,则函数图形的上色是根据函数值的大小进行。另外,Mathematica还提供了另外一种方法,可以根据指定的颜色函数(color
function)上色。
Plot3D[{f(x,y),
GrayLevel[s(x,y)]},{x,xmin,xmax},{y,ymin,ymax}]绘制三维图形,根据函数s(x,y)进行灰度上色
Plot3D[{f(x,y),
Hue[s(x,y)]},{x,xmin,xmax},{y,ymin,ymax}]绘制三维图形,根据函数s(x,y)上彩色
如何用Mathematica求极限
(1) 极限:
<--mstheme-->
<--mstheme-->
Limit[函数的表达式f(x),x->a]
<--mstheme-->
<--mstheme-->
(2) 单侧极限:
左极限:
<--mstheme-->
<--mstheme-->
Limit[函数的表达式f(x),x->a,Direction->1]
<--mstheme-->
<--mstheme-->
右极限:
<--mstheme-->
<--mstheme-->
Limit[函数的表达式f(x),x->a, Direction-> -1]
如何用Mathematica求导数
<--mstheme-->
D[f(x),x]
如何用Mathematica求高阶导数
<--mstheme-->
D[f(x),{x,n}]<--mstheme-->
在Mathematica中没有直接求隐函数导数的命令,但是我们可以根据数学中求隐函数导数的方法,在Mathematica中一步一步地进行推导。也可以自己编一个求隐函数导数的小程序。
在Mathematica中,没有直接求参数方程确定的函数的导数的命令,只能根据参数方程确定的函数的求导公式
一步一步地进行推导;或者,干脆自己编一个小程序,应用起来会更加方便。
如何用Mathematica求不定积分
<--mstheme-->
<--mstheme-->
Integrate[f(x),x] (或从工具栏输入 )
如何用Mathematica求定积分、广义积分
<--mstheme-->
<--mstheme-->
Integrate[f(x),{x,a,b}] (或从工具栏输入 )
<--mstheme-->
如何用Mathematica对数列和级数进行求和
Sum[f(n),{n, a, b}] (或从工具栏输入 )
Sum[f(n),{n, a, b, dn}]
Sum[f(n, m),{n, a, b},{m, c, d}]
Sum[f(n, m),{n, a, b, dn},{m, c, d, dm}]
如何用Mathematica进行连乘
Product[f(n),{n, a, b}] (或从工具栏输入 )
Product[f(n),{n, a, b, dn}]
Product[f(n, m),{n, a, b},{m, c, d}]
Product[f(n, m),{n, a, b, dn},{m, c, d, dm}]
如何用Mathematica展开级数
Series[f(x),{x ,a, n}]
如何在Mathematica中进行积分变换
LaplaceTransform[ f(t), t, s ] 拉普拉斯变换
InverseLaplaceTransform[ F(s), s, t ] 拉普拉斯变换的逆变换
FourierTransform[ f(t), t, ω] 傅立叶变换
InverseFourierTransform[ F(ω), ω, t ] 傅立叶变换的逆变换
ZTransform[ f(n), n, z] Z变换
InverseZTransform[ F(z), z, n ] Z变换的逆变换
FourierSinTransform[ f(t), t, ω] 傅立叶正弦变换
FourierCosTransform[ f(t), t, ω] 傅立叶余弦变换
InverseFourierSinTransform[ F(ω), ω, t ] 傅立叶正弦变换的逆变换
InverseFourierCosTransform[F(ω), ω, t] 傅立叶余弦变换的逆变换
如何用Mathematica解微分方程
DSolve[微分方程,y[x],x]
DSolve[{微分方程,初始条件或边界条件},y[x],x]
如何用Mathematica解微分方程组
DSolve[{微分方程组},{y1 [x],y2[x],…}, x]
DSolve[{微分方程组,初始条件或边界条件},{y1[x],y2[x],…},x]
如何用mathematica求多变量函数的极限
以两个变量为例说明,多于两个变量的函数极限可以依次类推。
Limit[Limit[f(x,y),x->a],y->b]计算极限
如何用mathematica求多元函数的偏导数
D[f,x1,x2,…, xn]求偏导数
如何用mathematica求多变量函数的泰勒展开式
Series[f,{x,x0,m},{y,y0,n},...]在x=x0,y=y0
,...处求函数f的泰勒展开式,其中m,n,...为展开的次数
如何用mathematica求重积分
Integrate[f,{x,a,b},{y,c,d},...,{z,m,n}]求重积分
NIntegrate[f,{x,a,b},{y,c,d},...,{z,m,n}]重积分的数值解
也可利用工具栏上的积分符号的组合来完成
如何用mathematica求梯度、散度、旋度
首先要加载CalculusVectorAnalysis函数库,加载方法为:
<<CalculusVectorAnalysis
以直角坐标系和三元函数为例说明
Grad[f, Cartesian[x,y,z] ]在直角坐标系中求纯量函数f的梯度,其中x,y,z为坐标变量
Div[f, Cartesian[x,y,z] ]在直角坐标系中求向量函数f={fx ,fy, fz}的散度,其中x,y,z为坐标变量
Curl[f, Cartesian[x,y,z] ]在直角坐标系中求向量函数f={fx ,fy, fz}的旋度,其中x,y,z为坐标变量
注:若把上面的Cartesian换为Cylindrical或Spherical,则表示在圆柱坐标系或球面坐标系中进行计算。
如何用Mathematica求函数的最大值和最小值
Maximize[f, {x, y, …}]求函数f关于变量x, y, …的最大值
Maximize[{f, conds}, {x, y, …}]在条件conds下,求函数f关于变量x, y, …的最大值
Minimize[f, {x, y, …}]求函数f关于变量x, y, …的最小值
Minimize [{f, conds}, {x, y, …}]在条件conds下,求函数f关于变量x, y, …的最小值
如何用mathematica求平均值
首先要加载StatisticsDescriptiveStatistics函数库,加载方法为:
<< StatisticsDescriptiveStatistics
或者加载整个统计函数库,加载方法为:
<<Statistics<br /> Mean[data]求数据data的算术平均数。数据data的格式为:{a1,a2,…}<br /> HarmonicMean[data]求数据data的调和平均数。数据data的格式为:{a1,a2,…}<br /> GeometricMean[data]求数据data的几何平均数。数据data的格式为:{a1,a2,…}<br /><br /> 如何用mathematica求中位数 <br /> 首先要加载StatisticsDescriptiveStatistics函数库,加载方法为:<br /> << StatisticsDescriptiveStatistics<br /> 或者加载整个统计函数库,加载方法为:<br /> <<Statistics
Median[data]求数据data的中位数。数据data的格式为:{ a1,a2,…}
如何用mathematica求众数
首先要加载StatisticsDescriptiveStatistics函数库,加载方法为:
<< StatisticsDescriptiveStatistics
或者加载整个统计函数库,加载方法为:
<<Statistics<br /> Mode[data]求数据data的众数。数据data的格式为:{ a1,a2,…}<br /><br /> 如何用mathematica求方差和标准差<br /> 首先要加载StatisticsDescriptiveStatistics函数库,加载方法为:<br /> << StatisticsDescriptiveStatistics<br /> 或者加载整个统计函数库,加载方法为:<br /> <<Statistics
Variance[data]求数据data的样本方差。数据data的格式为:{ a1,a2,…}
VarianceMLE[data]求数据data的母体方差。数据data的格式为:{ a1,a2,…}
StandardDeviation[data]求数据data的样本标准差。数据data的格式为:{a1,a2,…}
StandardDeviationMLE[data]求数据data的母体标准差。数据data的格式为:{ a1,a2,…}
如何用mathematica求协方差和相关系数
首先要加载StatisticsMultiDescriptiveStatistics函数库,加载方法为:
<< StatisticsMultiDescriptiveStatistics
或者加载整个统计函数库,加载方法为:
<<Statistics`
Covariance[data1,data2]求数据data1和data2的样本协方差。数据的格式为:{a1,a2,…}
CovarianceMLE[data1,data2]求数据data1和data2的母体协方差。数据的格式为:{a1,a2,…}
Correlation[data1,data2]求数据data1和data2的线性相关系数。数据的格式为:{a1,a2,…}
如何用mathematica进行曲线拟合
Fit[data,funs,vars]data表示待拟合的数据的集合,funs为变量vars的函数的集合,它们的格式如下:
data={{x1,y1},{x2,y2},…} (也可以是三维或三维以上空间的数据点)
data也可写成{y1,y2,…}的形式,此时,数据点是{{1,y1},{2,y2},…}
funs={f1,f2,f3,…}
该函数返回funs的一个线性组合用键盘快捷键(如 ** CTRL+/ 可用于分数的输入** )插入可填充的排版表达式:
(点击方框突出显示并填充,或按下 TAB 在各方框间移动.)
这是 输入指数 (CTRL+6) 、下标 (CTRL+-**) **和其他常见表达式的简单方法.
在笔记本中按下 ESC 键得到 符号,可用在键盘快捷输入形式 alias (在文档中常记为 ESCaliasESC )中.
键入正确的别名,当右侧的 输入完成后,表达式就会发生改变:
(偏微分 “partial derivative” 的别名是 “pd”.)
产生求和、积分和其他高级表达式的方法为:
(定积分 “definite integral” 的别名是 “dintt”.)

在桌面版的笔记本中,可以选择面板菜单中的“数学助手”查看可用的排版形式.
使用 TraditionalForm 命令以传统数学符号显示任意表达式:
| In[1]:= | 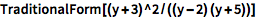
TraditionalForm[(y + 3)^2/((y - 2) (y + 5))]
| Out[1]= |  |
|---|
用 SHIFT+CMD+T 把现有单元转换成 TraditionalForm:
(TraditionalForm 形式的表达式仍然是可计算的.)
| In[2]:= | 
Limit[(x^2 - 1)/(x - 1), x -> 0]
| In[3]:= | 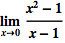
| Out[3]= |  来源:https://www.wolfram.com/language/fast-introduction-for-math-students/zh/mathematical-typesetting/ |
|---|
来源: https://www.wolfram.com/language/fast-introduction-for-math-students/zh/matrices-and-linear-algebra/
获得矩阵元素: ↩︎
必须用完全化简!!!:我遇到过这个问题,花了很长时间,以为自己算错了,其实没算错,只要用fullsimplify就能完全化简,得到的结果就和论文一致
对于科研中out1这样的复杂公式:
使用化简或因式分解都是不能得到和论文中的一样的结果,只有用fullsimplify完全化简的结果才和论文中的结果一样,所以以后必须只用fullsimplify完全化简!!!

(最后这个out9的结果才和论文中的一致) ↩︎
清除赋值:
对于上面出现的赋值的问题:
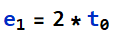 。唯一的清除这种符号的赋值的方法是:
。唯一的清除这种符号的赋值的方法是:
而不能用
 (此语法是清除数值的赋值)。
(此语法是清除数值的赋值)。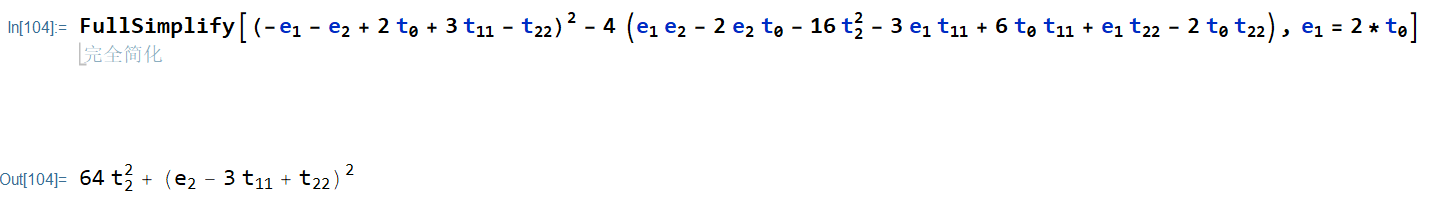

则:
 ,故确实清除了赋值!
,故确实清除了赋值!mathematica 中为变量的赋值时永久性的。
为避免程序的程序错误和节省资源,mathematica 中用完一个变量后就应该马上清除他。有两种个别地清除变量值的方法:
var=.Clear[var]
PS: 如果要清除函数,只有第二种方法会有效果。而清除带下标的变量,只有第一种方法有效果。 ↩︎
标签:mathematica,函数,归纳,expr,Mathematica,data,方法,加载 来源: https://www.cnblogs.com/quantum-condensed-matter-physics/p/16395139.html


