首页 > 其他分享> > AcWing 1273. 天才的记忆

AcWing 1273. 天才的记忆

2022-07-04 16:33:18 作者：互联网

AcWing 1273. 天才的记忆
题目传送门

一、$RMQ$问题

英文名称：$Range\ Maximum (Minimum)\ Query$，
含义:询问某个区间内的最大或最小值,一般采用$ST$算法，也称$ST$表、跳表。

二、$ST$算法

该问题，容易想到的解决方案是遍历，复杂度是$O(n)$。但当数据量非常大且查询很频繁时，该算法无法在有效的时间内查询出正解。

$ST$算法可以很好的解决这个问题。

算法步骤如下：

1、预处理

状态表示
设$a[i]$是要求区间最值的数列，$f[i, j]$表示从第$i$个数起连续$2^j$个数中的最大值。

举栗子：
$a$数列为：$$\large 3　 2　 4　 5　 6　 8　 1　 2　 9　 7　$$

$f[1,0]$表示第$1$个数起，长度为$2^0=1$的最大值，其实就是$3$这个数。
$f[1,1] = max(3,2) = 3$
$f[1,2]=max(3,2,4,5) = 5$
$f[1,3] = max(3,2,4,5,6,8,1,2) = 8$;

并且我们可以容易的看出$f[i,0]$就等于$a[i]$。（$dp$的初始值）

这样，动态规划的 状态、初值都已经有了，剩下的就是 状态转移方程 。

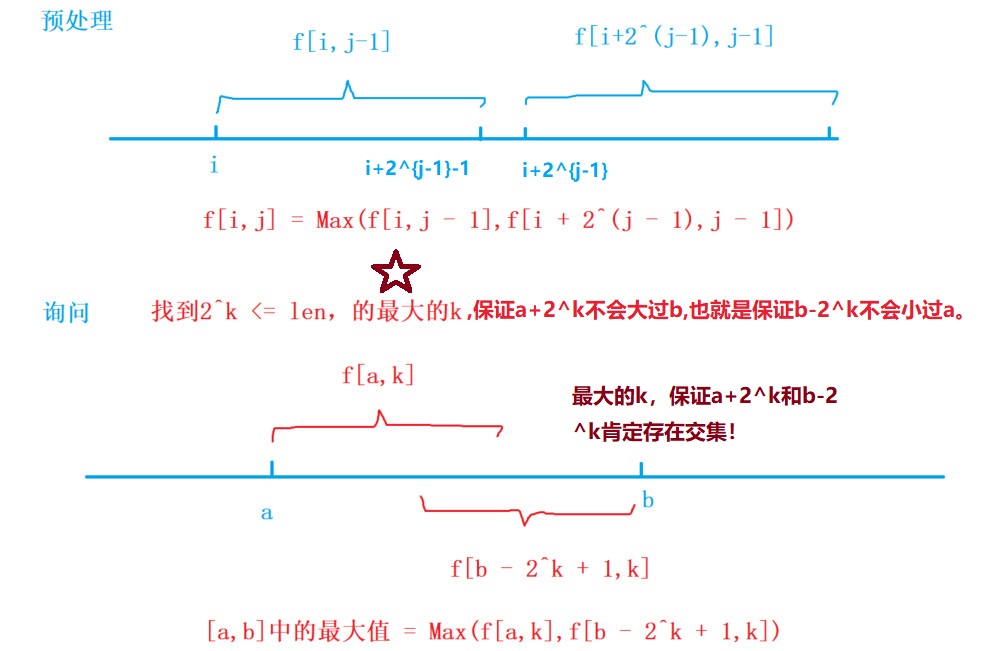
为什么$j$是外循环而$i$是内循环？
能不能调换一下嘞？
答案是 不可以 。

因为状态转移的时候$i$是跳动的，$j$是依赖于$j - 1$，因此需要先枚举$j$，再枚举$i$，还需要预处理出$2^k$的值.这一点在学习时需要特殊注意，这和此动态规划的具体含义相关，不能修改顺序。

查询

如何确定$k$呢？

对于每个查询 $[l,r]$，需要先找出最大的一个满足 $\large 2^k<len$ 的 $\large k$，其中
$len=r−l+1$，方法就是两边求对数：

\[\large log_2{2^k}<log_2(len) \\ \Rightarrow \\ k<log_2(len) \]

$k$要想取最大的整数，就是$(int)(log_2(len))$
如果是给整数赋值，就不用写强制转换，故直接写成：

int k = log2(len);

构造交集
查询时通过构建$2^k$的方法，造成$\large [a,a+2^k-1]$与$\large [b-2^k+1,b]$存在一个交集，分别求$f(a,k)$与$f(b-2^k+1,k)$，然后取一个$max$就是答案，虽然这里有一部分是重复的，但求最大值不怕重复！同时，也因为这个原因，使得$st$算法，也就只能用来计算最大最小值，不能用来处理其它需求。　

三、实现代码

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>

using namespace std;
const int N = 200010, M = 18;

int n, m;
int w[N];
int f[N][M];

void rmq_init() {
    for (int j = 0; j < M; j++)                     //注意是j在外层
        for (int i = 1; i + (1 << j) - 1 <= n; i++) // i在内层
            if (!j)                                 // base case 边界值
                f[i][j] = w[i];
            else
                f[i][j] = max(f[i][j - 1], f[i + (1 << j - 1)][j - 1]);
}

int query(int l, int r) {
    int len = r - l + 1;
    int k = log2(len);
    return max(f[l][k], f[r - (1 << k) + 1][k]);
}

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%d", &w[i]);

    rmq_init();

    scanf("%d", &m);
    while (m--) {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n", query(l, r));
    }
    return 0;
}

四、练习题

poj 3264 Balanced Lineup

标签：int,max,1273,ST,large,算法,天才,include,AcWing
来源： https://www.cnblogs.com/littlehb/p/16443377.html

AcWing 1273. 天才的记忆

一、\(RMQ\)问题

二、\(ST\)算法

1、预处理

查询

三、实现代码

四、练习题